CQOI 2018 解锁屏幕
洛谷 P4460 [CQOI2018]解锁屏幕
题目背景
使用过Android 手机的同学一定对手势解锁屏幕不陌生。Android 的解锁屏幕由3X3 个点组成,手指在屏幕上画一条线,将其中一些点连接起来,即可构成一个解锁图案。如下面三个例子所示:
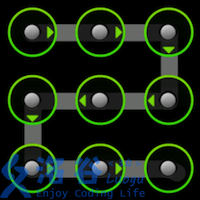
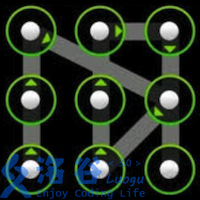
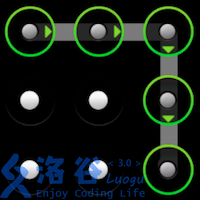
题目描述
画线时还需要遵循一些规则:
- 连接的点数不能少于4 个。也就是说只连接两个点或者三个点会提示错误。
- 两个点之间的连线不能弯曲。
- 每个点只能“使用”一次,不可重复。这里的“使用”是指手指划过一个点,该点变绿。
- 两个点之间的连线不能“跨过”另一个点,除非那个点之前已经被“使用”过了。
对于最后一条规则,参见下图的解释。左边两幅图违反了该规则; 而右边两幅图(分别为2->4-1-3-6 和6->5-4->1->9-2) 则没有违反规则,因为在“跨过”点时,点已经被“使用”过了。
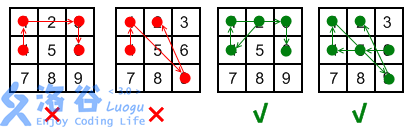
现在工程师希望改进解锁屏幕,增减点的数目,并移动点的位置,不再是一个九宫格形状,但保持上述画线的规则不变。请计算新的解锁屏幕上,一共有多少满足规则的画线方案。
输入格式
输入文件第一行,为一个整数n,表示点的数目。
接下来n 行,每行两个空格分开的整数x_ix**i 和y_iy**i,表示每个点的坐标。
输出格式
输出文件共一行,为题目所求方案数除以100000007 的余数。
输入输出样例
输入 #1复制
输出 #1复制
输入 #2复制
输出 #2复制
说明/提示
样例#1解释: 设4 个点编号为1到4,方案有1->2->3->4,2->1->3->4,3->2->1->4,2->3->1->4,及其镜像4->3->2->1,3->4->2->1,2->3->4->1,3->2->4->1。
对于30%的数据,1≤n≤101≤n≤10
对于100%的数据,-1000≤x_i,y_i≤1000,1≤n<20−1000≤x**i,y**i≤1000,1≤n<20。各点坐标不相同
题解:
七哥@littleseven 推荐的题。必须要做
看到方案数想到递推,然后\(1\le N\le 20\)。所以想到状态压缩。然后七哥让我推状态。我一想,如果开多维的话可能空间会爆,所以考虑只开一维,压成一个\(1<<n\)的状态,表示每个点是否被连接。
后来发现没法转移。所以考虑再开一维,于是到处搜索...拿什么做第二维能保证既能转移又不会挂空间呢?
一看数据范围,只有点数的二十还符合第二点要求,所以就选择这个做状态。苦思冥想看完题解之后,觉得把状态设置成这样最合适:
\(dp[i][j]\)表示点的选择状况为\(i\)、选择的点集中终点为\(j\)时的方案数。
那么,针对于一个已定的状态\(i\),它能转移的对象是这个状态中不为1的点。
举例:
\(dp[10010][2]\)可以转移到\(dp[11010][4],dp[10011][1]\)等状态。我们在转移的时候判一下这个点可不可以转移即可。(条件是转移前的\(j\)和转移后的\(j\)连上的直线上所有的点全部已经被到达过)
这样的话,我们可以先把两点间的点开\(vector\)存下,然后进行递推。
发现只连一个点的方案数是1.这个当初值。
我们转移的时候记录把当前状态用\(st\)记录下来,然后再用\(k\)枚举上一层状态,如果符合条件(即上面的点都被经过了,用\(flag\)标记判断进行转移就好)
转移方程是:
完整代码就是:
#include<cstdio>
#include<vector>
#include<algorithm>
using namespace std;
const int mod=1e8+7;
int n;
bool flag;
int dp[1<<20][21];
struct node
{
int x,y;
}a[21];
bool cmp(node a,node b)
{
if(a.x==b.x)
return a.y<b.y;
return a.x<b.x;
}
vector<int> vec[21][21];
bool check(node a,node b,node c)
{
return (a.x-b.x)*(b.y-c.y)==(b.x-c.x)*(a.y-b.y)?1:0;
}
int lowbit(int x)
{
int ret=0;
while(x)
{
x-=(x&(-x));
ret++;
}
return ret;
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
scanf("%d%d",&a[i].x,&a[i].y);
sort(a+1,a+n+1,cmp);
for(int i=1;i<=n;i++)
for(int j=i+1;j<=n;j++)
for(int k=i+1;k<j;k++)
if(check(a[i],a[k],a[j]))
vec[i][j].push_back(k);
for(int i=1;i<=n;i++)
dp[1<<(i-1)][i]=1;
for(int i=0;i<(1<<n);i++)
for(int j=1;j<=n;j++)
{
if((i>>(j-1))&1)
continue;
int st=(i|(1<<(j-1)));
for(int k=1;k<=n;k++)
{
if(k==j)
continue;
int xx=min(j,k);
int yy=max(j,k);
flag=0;
for(int t=0;t<vec[xx][yy].size();t++)
if(!((i>>(vec[xx][yy][t]-1))&1))
{
flag=1;
break;
}
if(flag)
continue;
dp[st][j]=(dp[st][j]+dp[i][k])%mod;
}
}
int ans=0;
for(int i=0;i<(1<<n);i++)
{
if(lowbit(i)<4)
continue;
for(int j=1;j<=n;j++)
ans=(ans+dp[i][j])%mod;
}
printf("%d",ans);
return 0;
}

