洛谷 P4710 「物理」平抛运动
洛谷 P4710 「物理」平抛运动
题目描述
小 F 回到班上,面对自己 28 / 110 的物理,感觉非常凉凉。他准备从最基础的力学学起。
如图,一个可以视为质点的小球在点 A(x_0, y_0)A(x0,y0) 沿 xx 轴负方向以某速度抛出,无视除重力外的所有阻力,最后恰好以速度 vv 砸到 B(0, 0)B(0,0) 点。
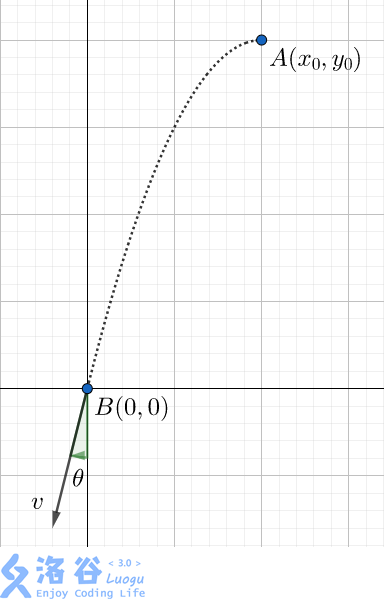
给定 vv 的大小与方向,你的任务是求出 (x_0,y_0)(x0,y0)。
给定的速度单位为 m \cdot s ^ {-1}m⋅s−1,重力加速度 g = 10 \ (m \cdot s ^ {-2})g=10 (m⋅s−2),请输出以 mm 为单位的答案。
如果你没有学过相关内容也没有关系,你可以从样例和提示里理解该题所求内容。
输入格式
输入一行,为两个最多 66 位的小数 v, \theta(1 \leq v \leq 100, 15 ^ \circ \leq \theta \leq 75 ^ \circ )v,θ(1≤v≤100,15∘≤θ≤75∘),即速度与图中所标角在弧度制下的大小。
输出格式
输出一行,两个最多 1515 位的小数 x_0, y_0x0,y0,为你的答案。
你的答案与参考答案的相对误差或者绝对误差小于 10 ^ {-3}10−3 即视为正确。
输入输出样例
输入 #1复制
输出 #1复制
说明/提示
样例解释
如图。
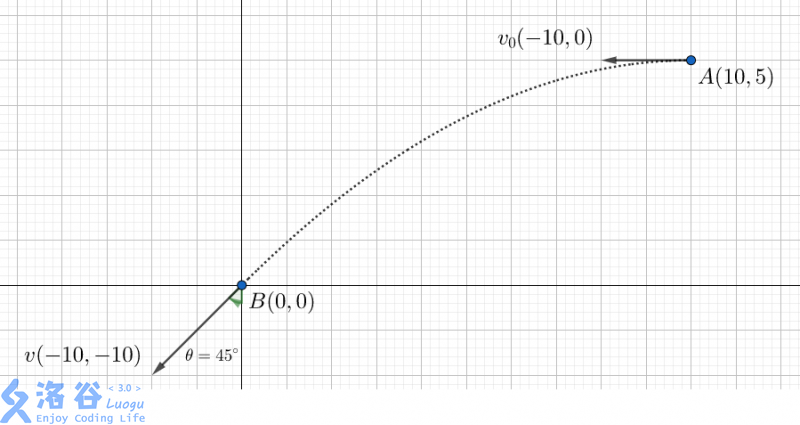
14.142136 \approx 10 \sqrt 2, 0.785398 \approx \frac \pi 4 = 45 ^ \circ .14.142136≈102,0.785398≈4π=45∘.
小球从 (10, 5)(10,5) 以速度 (-10, 0)(−10,0) 抛出,即可在 t = 1st=1s 时以 (-10, -10)(−10,−10) 砸在 (0, 0)(0,0)。
提示
如果你没有学习过相关内容,下面的内容可能有帮助:
zcy 教你学物理
首先,由于单位均为标准单位,所以所有结果均可以直接数字运算;视为质点意味着没有体积。
我们可以将小球速度分解,如图:
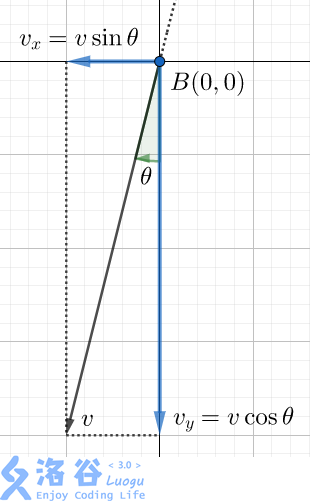
其中水平方向上的速度 v_xv**x 即为抛出速度,运动过程中一直为 v \sin \thetavsinθ;
垂直方向上的速度 v_yv**y 受重力加速,由 00 变化至 v \cos \thetavcosθ。
从抛出时开始计时,当时间为 tt 时,设此时水平、垂直方向上速度的大小分别为 v_{xt}, v_{yt}vxt,vyt,水平、垂直方向上位移的大小分别为 x_{xt}, x_{yt}xxt,xyt,有:
v_{xt} = v \sin \thetavxt=vsinθ
v_{yt} = gtvyt=g**t
x_{xt} = v_{xt}txxt=vxt**t
x_{yt} = \frac 1 2 g t ^ 2 = \frac 1 2{v_{yt}t}xyt=21g**t2=21vyt**t
当 tt 恰好是落地时间时,x_{xt}, x_{yt}xxt,xyt 即为答案。
关于弧度制:
\pi = 180 ^{\circ}π=180∘
也就是说:\frac \pi 2 = 90 ^{\circ}, \frac \pi 3 = 60 ^{\circ}, \ \cdots2π=90∘,3π=60∘, ⋯
关于三角函数:
如果你是 C/C++ 选手,你可以使用 math.h / cmath 里的 sin() cos() 进行计算;
如果你是 Pascal 选手,你可以使用 math 库(在 begin 前添加 uses math;)里的 sin() cos() 进行计算。
如果你是 Python 选手,你可以使用 math 库里的 math.sin() math.cos() 进行计算。
如果你是其他语言的选手,请参考相应文档。
题解:
这题真的是一道物理题...高一文化课蒟蒻表示不太会做...
但这题其实准备知识都告诉你了:平抛运动可以分解成一个自由落体运动和匀速直线运动。矢量运算用平行四边形法则正交分解法。那么我们就得到:
水平方向上的速度\(v_x\)为抛出的速度,运动过程中为\(v\times sin(\alpha)\)(原谅我不会打cita)。而垂直方向上的速度还要加一个加速度\(g=10m/s^2\).那么就是从\(0\rightarrow v\times cos(\alpha)\)。很容易得出,这个东西还跟时间有关系。
从抛出的时候开始计时:当时间为\(t\)时,设此时的水平、竖直方向上的速度大小分别为:\(v_x,v_y\).
那么有:
所以,可以通过上面的那些式子搞吧搞吧得到一个运动时间的式子:
因为在水平方向质点相当于做匀速直线运动,所以水平方向上的位移\(x_0\)可以被表示为:
根据三角形相似,对应边成比例,所以有:
变形:
所有的式子都在上面了,通过已知量可以解出两个未知量:\(x_0,y_0\)。
代码如下:
#include<cmath>
#include<cstdio>
double v,cita,vx,vy,t,x2;
const double g=10.0;
int main()
{
scanf("%lf%lf",&v,&cita);
vy=v*cos(cita);
vx=v*sin(cita);
t=vy/g;
x2=v*sin(cita)*t;
printf("%.3lf %.3lf\n",x2,(x2/2)*vy/vx);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号