CF1010D Mars rover
CF1010D Mars rover
题目描述
Natasha travels around Mars in the Mars rover. But suddenly it broke down, namely — the logical scheme inside it. The scheme is an undirected tree (connected acyclic graph) with a root in the vertex 11 , in which every leaf (excluding root) is an input, and all other vertices are logical elements, including the root, which is output. One bit is fed to each input. One bit is returned at the output.
There are four types of logical elements: AND ( 22 inputs), OR ( 22 inputs), XOR ( 22 inputs), NOT ( 11 input). Logical elements take values from their direct descendants (inputs) and return the result of the function they perform. Natasha knows the logical scheme of the Mars rover, as well as the fact that only one input is broken. In order to fix the Mars rover, she needs to change the value on this input.
For each input, determine what the output will be if Natasha changes this input.
输入格式
The first line contains a single integer nn ( 2 \le n \le 10^62≤n≤106 ) — the number of vertices in the graph (both inputs and elements).
The ii -th of the next nn lines contains a description of ii -th vertex: the first word "AND", "OR", "XOR", "NOT" or "IN" (means the input of the scheme) is the vertex type. If this vertex is "IN", then the value of this input follows ( 00 or 11 ), otherwise follow the indices of input vertices of this element: "AND", "OR", "XOR" have 22 inputs, whereas "NOT" has 11 input. The vertices are numbered from one.
It is guaranteed that input data contains a correct logical scheme with an output produced by the vertex 11 .
输出格式
Print a string of characters '0' and '1' (without quotes) — answers to the problem for each input in the ascending order of their vertex indices.
输入输出样例
输入 #1复制
输出 #1复制
说明/提示
The original scheme from the example (before the input is changed):
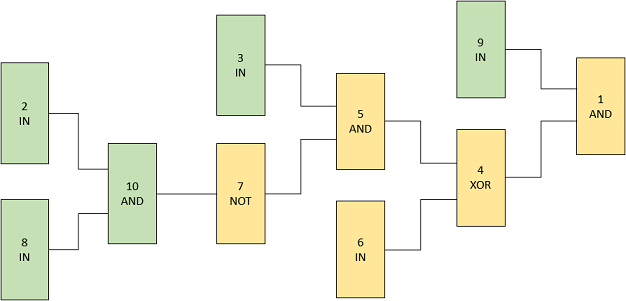
Green indicates bits '1', yellow indicates bits '0'.
If Natasha changes the input bit 22 to 00 , then the output will be 11 .
If Natasha changes the input bit 33 to 00 , then the output will be 00 .
If Natasha changes the input bit 66 to 11 , then the output will be 11 .
If Natasha changes the input bit 88 to 00 , then the output will be 11 .
If Natasha changes the input bit 99 to 00 , then the output will be 00 .
题解:
2019.10.24模拟赛T2 30分暴力场
写在前面
看了其他人的题解,非常的难受。
见过一些大佬的签名是这么写的:想要变得牛X,得先把自己当成傻X。
特别喜欢这句话,虽然有些粗鄙。
请不要把自己会做的题都归为傻X题。不论这道题是不是真的那么简单。因为每个人和每道题目都需要足够的尊重。大家都年轻过,都曾经从零开始。请想一想那时的自己看到自己现在的置评时会是什么感觉。
这也是我来发这篇题解的原因。
正文
暴力分只要理解好题意就可以拿:可以看出来就是一个简单的深搜,每个节点存一个结构体:操作、左右儿子。(叶子节点的话存值),然后直接开搜,时间复杂度大约是\(O(n^2)\)的,大约只能过30分...(模糊.jpg)
代码如下:(考场版)
#include<cstdio>
#include<cstring>
#include<iostream>
using namespace std;
const int maxn=1e6+10;
int n;
struct node
{
char opt[10];
int a,b;
}t[maxn];
int dfs(int x)
{
if(t[x].opt[1]=='A')
return dfs(t[x].a)&dfs(t[x].b);
else if(t[x].opt[1]=='O')
return dfs(t[x].a)|dfs(t[x].b);
else if(t[x].opt[1]=='X')
return dfs(t[x].a)^dfs(t[x].b);
else if(t[x].opt[1]=='N')
return !dfs(t[x].a);
else
return t[x].a;
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%s",t[i].opt+1);
if(t[i].opt[1]=='A' || t[i].opt[1]=='X' || t[i].opt[1]=='O')
scanf("%d%d",&t[i].a,&t[i].b);
else
scanf("%d",&t[i].a);
}
for(int i=1;i<=n;i++)
if(t[i].opt[1]=='I')
{
t[i].a=!t[i].a;
printf("%d",dfs(1));
t[i].a=!t[i].a;
}
return 0;
}
我们重新来看这道题。数据是\(10^6\)的,这是\(O(n)\)或\(O(nlogn)\)的数据范围,\(O(n)\)做法比较不现实,我们用\(log\)的。一看\(log\)的数据结构,我们应该想到和二有关的一些技巧、算法和数据结构,倍增、树形结构等等。再结合这道题的题目:应该就是树形结构。
带着这个幻想,我们开始重新审题:这是一棵“运算树”。手推几组数据,我们不难发现:如果一个叶子节点被更改影响到,那么可以肯定的是,这个叶子节点到根节点的链(这个链是唯一的)的所有值都会被取反。那么我们来看这些操作,当操作为非或者异或的时候,那么这个节点的值会被取反(任意一个儿子被修改即可)。反之,如果操作为与或或,必须两个儿子的值都被修改,才能被取反。
具体的实现方法是:在每个节点加一个标记数组,表示这个点会不会随着儿子节点的权值变化而变化:如果这个数组的值为1,表示这个节点会随着儿子的值变化而变化,为0则相反。然后就是线段树的过程:如果一个节点为0,那么就把其所有子节点的标记全置成0(则无论怎么改都不会对其造成影响)。反之就下传标记(继续判下面的儿子们)
代码如下:
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
const int maxn=1e6+10;
int n,ans[maxn],opt[maxn],son[maxn][2],val[maxn];
bool v[maxn];
int turn(char s[])
{
if(s[0]=='I')
return 1;
if(s[0]=='N')
return 2;
if(s[0]=='O')
return 3;
if(s[0]=='A')
return 4;
if(s[0]=='X')
return 5;
}
int dfs1(int u)
{
if(opt[u]==1)
return val[u];
if(opt[u]==2)
return(val[u]=!dfs1(son[u][0]));
if(opt[u]==3)
return(val[u]=(dfs1(son[u][0])|dfs1(son[u][1])));
if(opt[u]==4)
return(val[u]=(dfs1(son[u][0])&dfs1(son[u][1])));
if(opt[u]==5)
return(val[u]=(dfs1(son[u][0])^dfs1(son[u][1])));
}
void dfs2(int u)
{
if(v[u]==0)
v[son[u][0]]=v[son[u][1]]=0;
else
{
switch(opt[u])
{
case 2:
v[son[u][0]]=1;
break;
case 3:
if(val[son[u][0]])
v[son[u][1]]=0;
else
v[son[u][1]]=1;
if(val[son[u][1]])
v[son[u][0]]=0;
else
v[son[u][0]]=1;
break;
case 4:
if(!val[son[u][0]])
v[son[u][1]]=0;
else
v[son[u][1]]=1;
if(!val[son[u][1]])
v[son[u][0]]=0;
else
v[son[u][0]]=1;
break;
case 5:
v[son[u][0]]=v[son[u][1]]=1;
break;
}
}
v[0]=0;
if(son[u][0])
dfs2(son[u][0]);
if(son[u][1])
dfs2(son[u][1]);
}
int main()
{
memset(v,1,sizeof(v));
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
char s[10];
scanf("%s",s);
opt[i]=turn(s);
if(opt[i]==1)
scanf("%d",&val[i]);
else if(opt[i]==2)
scanf("%d",&son[i][0]);
else
scanf("%d%d",&son[i][0],&son[i][1]);
}
dfs1(1);
v[1]=1;
dfs2(1);
for(int i=1;i<=n;i++)
if(opt[i]==1)
printf("%d",val[1]^v[i]);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号