浅谈树链剖分
浅谈树链剖分
本篇随笔讲解图论中的树链剖分相关内容。
树链剖分是树上问题的极常用操作,可以说不会树链剖分,一半以上的树上难题都毫无思路。其重要性不言而喻。想要流畅阅读本篇博客并学习树链剖分,需要读者具有一定的图论基础,并对树形结构和深搜算法有基本的认识。由于本蒟蒻的水平可能不足支持强大的树剖的讲解,所以题解中的一些不足之处敬请大佬们指正。
树链剖分的基本概念
树链剖分,顾名思义,就是把树拆成链。根据树的形态,我们可以很容易的发现,任何一棵树都会有很多条链正好把树完全拆分。但是树链剖分并不是单单地把树拆成链。它拆出的链有“轻重之分”。
那么什么是轻重链呢?
这就涉及到了树链剖分的一些基本概念名词,如下述。
- 重儿子:我们知道,除叶子节点之外,每个节点都会有若干个儿子节点,而只要这个节点不是叶子节点,它都是一棵子树的根。那么,这个父亲节点就有很多个儿子,而一定会有一个儿子的儿子最多,也就是子树最大。那么这个儿子节点就叫做\(x\)的重儿子。
- 轻儿子:与重儿子对照理解,重儿子是唯一的,除了重儿子之外的所有儿子都是轻儿子。
- 重边:父节点与重儿子组成的边(需要注意的是,这里的父节点不一定也是重儿子)
- 轻边:除重边之外的边。
- 重链:由重边连起来的链叫做重链,特别地,一条重链的顶部是一个轻儿子。
- 轻链:由轻边连起来的链叫做轻链。
我们可以通过一张图来直观理解:
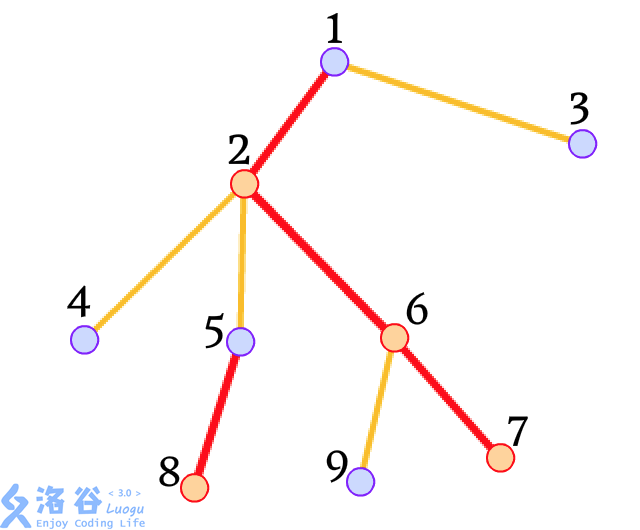
树链剖分解决的问题
树链剖分是树状结构的操作,自然解决的是树上问题。根据我们以上讲述的基本概念,我们发现我们可以将一棵树进行轻重链的树链剖分。然后我们就可以把一条链上的节点处理成区间的形式(这个理解非常重要!)从而把树上的问题转化成了区间问题进行求解。至于区间问题,我们可以采用一些数据结构求解,比如线段树、树状数组等。
一般来讲,树链剖分可以解决以下问题:
-
修改两点路径上各点的值
-
查询两点路径上各点的值
-
修改某点子树上各点的值
-
查询某点子树上各点的值
-
求解LCA问题
树链剖分的深搜预处理
根据以上的概念理解,我们会发现,若要求解以上问题,我们用树链剖分的好处就是把树上问题变成区间问题,而区间问题可以用数据结构求解,比如线段树。但是区间需要编号连续,如果用原树的节点编号来进行“区间求解”,那显然是不行的。因为一条链上的节点可能是“3.5.7.8.2.1”这样的乱序,而不是我们想要的一段“连续的数列”,所以这时不能转换成线段树求解。为了让区间连续,我们对整棵树进行预处理。
树链剖分的核心操作也是预处理。
对于任意节点\(x\),我们通过DFS处理出它的深度,子树大小,重儿子编号和父节点编号。这些东西可以用一次深搜处理出来。实质上就是一个树上遍历的过程。
我们用\(deep[]\)表示深度,\(size[]\)表示子树大小,\(son[]\)表示重儿子是谁(编号),以及\(fa[]\)表示父节点是谁(编号)。
代码:
void dfs1(int x,int f)
{
fa[x]=f;
size[x]=1;
deep[x]=deep[f]+1;
for(int i=head[x];i;i=nxt[i])
{
int y=to[i];
if(y==f)
continue;
dfs1(y,x);
size[x]+=size[y];
if(son[x]==0 || size[y]>size[son[x]])
son[x]=y;
}
}
但是为了进行树链剖分的相关操作,仅仅处理出这些数据是远远不够的。因为有了这些数据,我们只知道了重链的相关信息,却依然不能维护出我们需要的那段“连续的区间”。所以,我们需要第二遍深搜。
如何在深搜中保证链上节点编号连续呢?
根据深搜的性质和重链的性质,我们已经可以隐隐约约的猜到:用DFS序即可。
关于DFS序的相关知识,如有不懂请参照本蒟蒻的这篇博客:
也就是说,我们必然会进行第二遍DFS,而第二遍DFS要处理出的东西就是:每条链的顶端节点,每个点的DFS序新编号。
我们用\(top[]\)数组表示每个节点所在链的顶端是谁,\(id[]\)数组表示节点的DFS序新编号。
所以有了以下代码:
void dfs2(int x,int t)
{
id[x]=++cnt;
top[x]=t;
if(!son[x])
return;
dfs2(son[x],t);
for(int i=head[x];i;i=nxt[i])
{
int y=to[i];
if(y==fa[x] || y==son[x])
continue;
dfs2(y,y);
}
}
这里有必要说明一下:
我们先处理重儿子后处理轻儿子。
为什么呢?
因为我们最终的目的是把链的新的DFS编号变成连续的。这样,我们先处理重链再处理轻链,就能做到:每一条重链上的编号是连续的,同时,每一棵子树上的编号也是连续的。
以上就是树链剖分的核心操作:预处理(预处理竟然变成了核心操作)
树链剖分操作详解
之后我们回顾一下树链剖分所解决的问题:
-
修改两点路径上各点的值
-
查询两点路径上各点的值
-
修改某点子树上各点的值
-
查询某点子树上各点的值
通过刚才的预处理,我们已经把树上节点的新编号变成了连续的。然后我们就可以针对区间(链)把原树变成线段树来进行我们要做的一系列操作。
先来一份线段树的基本代码:
(包括建树、递归修改、递归查询、lazy标记)
void build(int pos,int l,int r)
{
int mid=(l+r)>>1;
if(l==r)
{
tree[pos]=w[l];
return;
}
build(lson,l,mid);
build(rson,mid+1,r);
tree[pos]=(tree[lson]+tree[rson]);
}
void mark(int pos,int l,int r,int k)
{
tree[pos]+=(r-l+1)*k;
lazy[pos]+=k;
}
void pushdown(int pos,int l,int r)
{
int mid=(l+r)>>1;
mark(lson,l,mid,lazy[pos]);
mark(rson,mid+1,r,lazy[pos]);
lazy[pos]=0;
}
void update(int pos,int l,int r,int x,int y,int k)
{
int mid=(l+r)>>1;
if(x<=l && r<=y)
{
mark(pos,l,r,k);
return;
}
pushdown(pos,l,r);
if(x<=mid)
update(lson,l,mid,x,y,k);
if(y>mid)
update(rson,mid+1,r,x,y,k);
tree[pos]=(tree[lson]+tree[rson]);
}
int query(int pos,int l,int r,int x,int y)
{
int mid=(l+r)>>1;
int ret=0;
if(x<=l && r<=y)
return tree[pos];
pushdown(pos,l,r);
if(x<=mid)
ret+=query(lson,l,mid,x,y);
if(y>mid)
ret+=query(rson,mid+1,r,x,y);
return ret;
}
如果读者已经对线段树非常熟悉,那么就会发现:在经过树链剖分的预处理之后,对于上述的4个操作,我们只需要把节点的新编号(新编号在树上是按链连续的)映射到一个数列上,然后对数列进行线段树的上述操作即可。
树链剖分求LCA
讲这个是为了为下面的链上修改做铺垫。
树链剖分求LCA是比较快速的做法,它的实现原理也比较好理解:
我们每次求LCA(x,y)的时候就可以判断两点是否在同一链上
如果两点在同一条链上我们只要找到这两点中深度较小的点输出就行了(废话)
如果两点不在同一条链上:
那就找到深度较大的点令它等于它所在的链顶端的父节点即为x=fa[top[x]]:
直到两点到达同一条链上,输出两点中深度较小的点即可。
链上修改
对于一个修改任意两点最短路径上的所有点的操作,我们的一个朴素思路是求出两点的LCA,然后进行修改。
这就是为什么讲树链剖分求LCA。因为链上修改是基于求LCA操作的。
相比于树链剖分求LCA,链上修改只是加了个线段树的操作而已。
或许代码能帮你理解一下:
void upd_chain(int x,int y,int k)
{
while(top[x]!=top[y])
{
if(deep[top[x]]<deep[top[y]])
swap(x,y);
update(1,1,n,id[top[x]],id[x],k);//attention
x=fa[top[x]];
}
if(deep[x]<deep[y])
swap(x,y);
update(1,1,n,id[y],id[x],k);//attention
}
ATTENTION
这里需要注意的是update时的节点编号问题,以为重新编号是基于DFS序的基础的,所以根据深搜的性质,每个节点的\(top[]\)肯定要比这个节点的新编号小。
下面的\(id[x],id[y]\)也是这个道理,千万不要写反!!
链上查询
链上查询的基本实现思路与链上修改大同小异。
直接放代码:
int q_chain(int x,int y)
{
int ret=0;
while(top[x]!=top[y])
{
if(deep[top[x]]<deep[top[y]])
swap(x,y);
(ret+=query(1,1,n,id[top[x]],id[x]))%=mod;
x=fa[top[x]];
}
if(deep[x]<deep[y])
swap(x,y);
(ret+=query(1,1,n,id[y],id[x]))%=mod;
return ret;
}
树上修改/查询
树上修改/查询并不需要那么复杂的操作。我们进行树上修改/查询主要运用了树链剖分的一个性质:
以某一个节点为根的子树编号是这个节点+这个节点的\(size[]\)-1.
即新树映射到数列上,一棵子树所占的区间是:\([id[x],id[x]+size[x]-1]\).
这样就很容易写树上修改/查询的代码了:
void upd_subtree(int x,int k)
{
update(1,1,n,id[x],id[x]+size[x]-1,k);
}
int q_subtree(int x)
{
return query(1,1,n,id[x],id[x]+size[x]-1);
}
在这里再向大家推荐模板例题:洛谷3384
熟练运用树链剖分并解决实际问题是一个提高组/省选选手所必须的一个素质。希望这篇随笔能帮到正在\(OI\)路上奋斗的你(耶比)。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号