JSOI 2010 连通数
洛谷 P4306 [JSOI2010]连通数
题目描述
度量一个有向图联通情况的一个指标是连通数,指图中可达顶点对个的个数。
如图
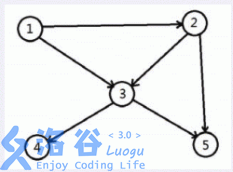
顶点 11 可达 1,2,3,4,51, 2, 3, 4, 5
顶点 22 可达 2,3,4,~52, 3, 4, 5
顶点 33 可达 3,4,53, 4, 5
顶点 4,~54, 5 都只能到达自身。
所以这张图的连通数为 1414。
给定一张图,请你求出它的连通数
输入格式
输入数据第一行是图顶点的数量,一个正整数N。 接下来N行,每行N个字符。第i行第j列的1表示顶点i到j有边,0则表示无边。
输出格式
输出一行一个整数,表示该图的连通数。
输入输出样例
输入 #1复制
输出 #1复制
说明/提示
对于100%的数据,N不超过2000。
题解:
好不容易碰上一道紫水题
人生中首次自己自主AC紫题,感觉比我国爆破第一颗原子弹还激动...
大家都使用的tarjan缩点、反向建图等正解做法,但是这些复杂图论我不是很会。
我一开始想到的是SPFA,我每个点跑一遍最短路,跑完之后开始从1到n扫,如果dist数组被更新了就说明此点可达,累加ans。
最后直接输出即可
数据还是比较水的,请求洛谷加强数据,我这个算法的时间复杂度奇高,预期TLE5个点,但是竟然AC了...
代码:
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
int n,ans;
char s[2010];
int tot,to[4000001],nxt[4000001],head[2001];
int dist[2001],v[2001];
void add(int x,int y)
{
to[++tot]=y;
nxt[tot]=head[x];
head[x]=tot;
}
void spfa(int start)
{
for(int i=1;i<=n;i++)
dist[i]=1e9,v[i]=0;
queue<int> q;
q.push(start);
v[start]=1;
dist[start]=0;
while(!q.empty())
{
int x=q.front();
q.pop();
v[x]=0;
for(int i=head[x];i;i=nxt[i])
{
int y=to[i];
if(dist[y]>dist[x]+1)
{
dist[y]=dist[x]+1;
if(v[y]==0)
q.push(y),v[y]=1;
}
}
}
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%s",s+1);
for(int j=1;j<=n;j++)
if(s[j]=='1')
add(i,j);
}
for(int i=1;i<=n;i++)
{
spfa(i);
for(int j=1;j<=n;j++)
if(dist[j]<1e9)
ans++;
}
printf("%d",ans);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号