杨辉三角—知识点详解

杨辉三角

杨辉三角（欧洲叫帕斯卡三角）是一个很奇妙的东西，它是我国数学家杨辉在1261年发现的，欧洲的帕斯卡于1654年发现，比我国的巨佬数学家杨辉晚了393年。（在此show一下我的爱国情怀）

铺垫知识

(1)二项式系数

二项式系数，定义为\((1+x)^n\)展开之后\(x\)的系数。

通常来讲，二项式系数代表的是从\(n\)件物品中，无序地选取\(k\)件的方法总数，如果你读过我全排列的博客链接，那么你会发现，这就是我们定义的“组合数”。

证明也比较简单：

我们假设上述的\(n=4，k=2\)，通过组合数公式可以得出组合数为6.

假如我们把\((1+x)^4\)展开并标记每一个\(x\)，就会得到：

\[(1+x_1)(1+x_2)(1+x_3)(1+x_4) \]

上式等于：

\[(1+x_1)\cdots(1+x_4)=\cdots+x_1x_2+x_1x_3+x_1x_4+x_2x_3+x_2x_4+x_3x_4+\cdots \]

我们发现，假如把标记去掉，这个\(x^2\)的系数正好等于6.

也就证明了：\((1+x)^n\)中\(x^k\)的系数正好等于从\(n\)个元素中选取\(k\)个元素的组合数（\(C_n^k\)）.

杨辉三角性质

杨辉三角（帕斯卡三角），是二项式系数在三角形中的几何排列。我们看一发杨辉三角的图，并在此图上进行后续的讲解：（版权：转载自百度）

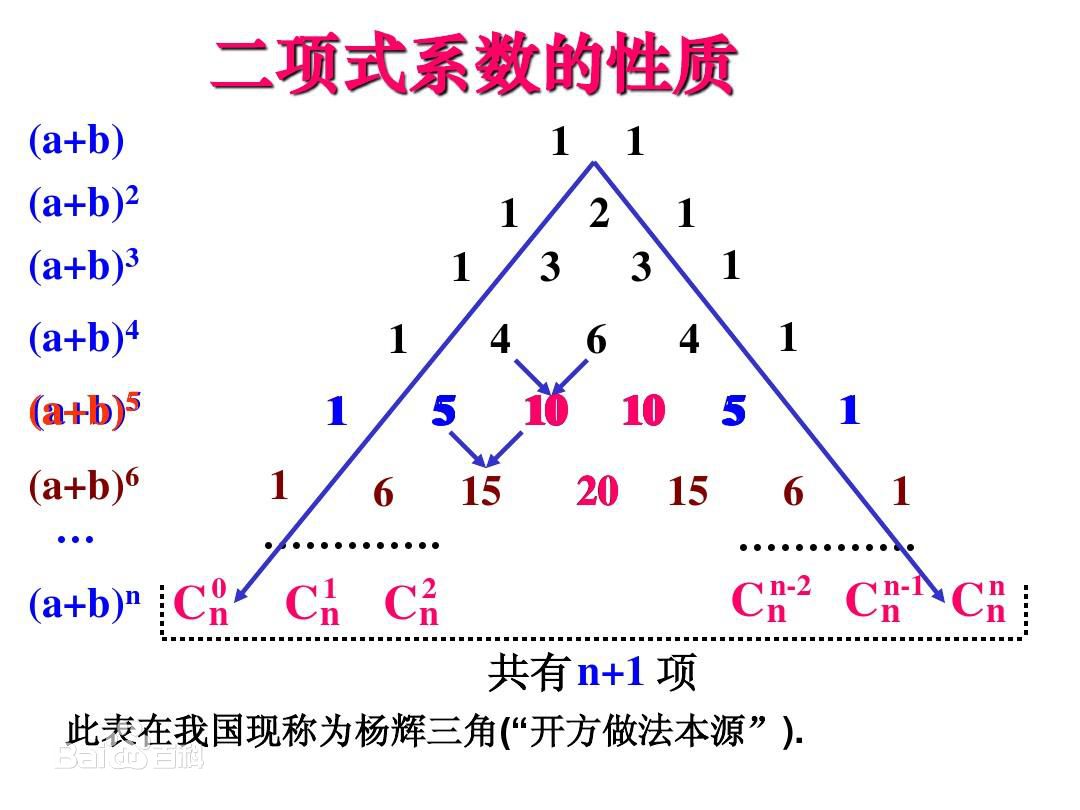
我们从这张杨辉三角示意图上发现，杨辉三角的每行行首与每行结尾的数都为1.而且，每个数等于其左上及其右上二数的和。这样我们发现，杨辉三角左右对称。

那么我们就可以通过这些基本概念把这个杨辉三角同我们所说的组合数即二项式系数联系在一起：

通过刚才的知识铺垫，我们发现，第i行的第j个数，我们可以用\(C_{i}^{j}\)来表示从\(i\)个元素中选取\(j\)个元素的组合数。（注意，这里的第i行是从0计数）并且，由于对称性，我们可以发现，杨辉三角中第n行的第m个数恒等于本行的第n-m+1个数。

与二项式系数知识点进行结合，我们会发现\((1+x)^n\)展开后，各次数的系数正好对应第\(n\)行的每一项。

杨辉三角代码实现的递推公式

在很多题目中，我们常常需要用打表的形式先处理出杨辉三角矩阵，然后再以此为基础进行程序求解。那么我们打表的时候如果手存表格的话，不仅浪费考试时间，而且保证不了空间范围和正确性，这个时候需要我们使用递推的手段用程序处理出表格。

根据杨辉三角的性质，我们推出以下的递推公式：（如果看完了上面这些，这个还看不懂的话，就退役吧）

\[C[i][j]=C[i-1][j]+C[i-1][j-1]; \]

杨辉三角的基本知识点大约是这个样子。

大家需要用一些例题巩固。