NOIP 2008 立体图
洛谷 P1058 立体图
JDOJ 1541: [NOIP2008]立体图 T4
题目描述
小渊是个聪明的孩子,他经常会给周围的小朋友们将写自己认为有趣的内容。最近,他准备给小朋友们讲解立体图,请你帮他画出立体图。
小渊有一块面积为m \times nm×n的矩形区域,上面有m \times nm×n个边长为11的格子,每个格子上堆了一些同样大小的积木(积木的长宽高都是11),小渊想请你打印出这些格子的立体图。我们定义每个积木为如下格式,并且不会做任何翻转旋转,只会严格以这一种形式摆放:
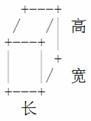
每个顶点用11个加号’++’表示,长用33个”-−”表示,宽用11个”/”,高用两个”|”表示。字符’++’,”-−”,”/”,”|”的ASCIIASCII码分别为4343,4545,4747,124124。字符’.’(ASCIIASCII码4646)需要作为背景输出,即立体图里的空白部分需要用’.’来代替。立体图的画法如下面的规则:
若两块积木左右相邻,图示为:
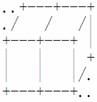
若两块积木上下相邻,图示为:
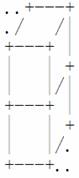
若两块积木前后相邻,图示为:

立体图中,定义位于第(m,1(m,1)的格子(即第mm行第11列的格子)上面自底向上的第一块积木(即最下面的一块积木)的左下角顶点为整张图最左下角的点。
输入格式
第一行有用空格隔开的22个整数mm和nn,表示有m \times nm×n个格子(1 \le m,n \le 50)(1≤m,n≤50)。
接下来的mm行,是一个m \times nm×n的矩阵,每行有nn个用空格隔开的整数,其中第ii行第jj列上的整数表示第ii行第jj列的个子上摞有多少个积木(1 \le1≤每个格子上的积木数\le 100≤100)。
输出格式
输出包含题目要求的立体图,是一个KK行LL列的字符串矩阵,其中KK和LL表示最少需要KK行LL列才能按规定输出立体图。
输入输出样例
输入 #1复制
输出 #1复制
说明/提示
NOIP2008普及组第四题
题解:
一道非常好的模拟大题。
这道题乍一看给人一种无从下手的感觉,但是理清思路,明白步骤之后就非常好做。
首先我们明白,这道题的实质就是打印一张符合要求的立方体视图。
所以我们一定要明白这个东西的长宽。
长度k,需要被不断更新,由输入而定。
宽度l只由n,m决定,其公式为4m(一个块的底边长5(需要减一))+2n(一个块的宽度映射下来是2),最后还要加上1。
(不明白的看图示)
宽度k是同理的。
然后我们考虑用数组的形式输出,先把要输出的内容存到一个数组里,最后直接打印k行l列的数组就可以了/
初始化的时候要置成“·”
然后就是要放正方体,放正方体的时候有这么几个难点:首先,怎么打印正方体,其次,怎么考虑覆盖的问题(可以理解成遮掩)。
我们把每一个正方体打进一个表里(解决问题1)
然后从后往前放正方体(覆盖的话就直接覆盖掉了)
然后我们得出AC代码。
#include<cstdio>
#include<algorithm>
using namespace std;
int n,m,k,l,x,y;
char block[6][8]=
{
"..+---+",
"./ /|",
"+---+ |",
"| | +",
"| |/.",
"+---+..",
};
int a[55][55];
char map[550][550];
void init(int x,int y)
{
for(int i=0;i<6;i++)
for(int j=0;j<7;j++)
if(block[6-i-1][j]!='.')
map[x-i][y+j]=block[6-i-1][j];
}
int main()
{
scanf("%d%d",&n,&m);
l=4*m+2*n+1;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
{
scanf("%d",&a[i][j]);
k=max(k,a[i][j]*3+2*(n-i+1)+1);
}
for(int i=1;i<=k;i++)
for(int j=1;j<=l;j++)
map[i][j]='.';
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
{
x=k-2*(n-i);
y=2*(n-i)+4*(j-1)+1;
while(a[i][j]--)
{
init(x,y);
x-=3;
}
}
for(int i=1;i<=k;i++)
{
for(int j=1;j<=l;j++)
printf("%c",map[i][j]);
printf("\n");
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号