NOI 2001 食物链
洛谷 P2024 [NOI2001]食物链
JDOJ 1555: VIJOS-P1531 食物链
JDOJ 1047: 食物链
Description
动物王国中有三类动物A,B,C,这三类动物的食物链构成了有趣的环形。A吃B, B吃C,C吃A。 现有N个动物,以1-N编号。每个动物都是A,B,C中的一种,但是我们并不知道它到底是哪一种。 有人用两种说法对这N个动物所构成的食物链关系进行描述: 第一种说法是“1 X Y”,表示X和Y是同类。 第二种说法是“2 X Y”,表示X吃Y。 此人对N个动物,用上述两种说法,一句接一句地说出K句话,这K句话有的是真的,有的是假的。当一句话满足下列三条之一时,这句话就是假话,否则就是真话。 1) 当前的话与前面的某些真的话冲突,就是假话; 2) 当前的话中X或Y比N大,就是假话; 3) 当前的话表示X吃X,就是假话。 你的任务是根据给定的N(1<=N<=50,000)和K句话(0<=K<=100,000),输出假话的总数。
Input
第一行是两个整数N和K,以一个空格分隔。 以下K行每行是三个正整数 D,X,Y,两数之间用一个空格隔开,其中D表示说法的种类。 若D=1,则表示X和Y是同类。 若D=2,则表示X吃Y。
Output
只有一个整数,表示假话的数目。
Sample Input
100 7 1 101 1 2 1 2 2 2 3 2 3 3 1 1 3 2 3 1 1 5 5
Sample Output
3
HINT
输入文件 对7句话的分析
100 7
1 101 1 假话
2 1 2 真话
2 2 3 真话
2 3 3 假话
1 1 3 假话
2 3 1 真话
1 5 5 真话
题解:
这是一道种类并查集的练手题。
我们知道,并查集可以维护连通性和传递性,就是维护同类之间的关系——亲戚的亲戚是亲戚。
而种类并查集可以维护对立关系,即“敌人的敌人是朋友”。
我们实现的方法是将并查集扩大一倍的范围,然后划分成两个不同的种类。
在同种类的并查集中合并,就是正常的合并操作。
在不同种类的并查集中合并,就是种类并查集中“敌人”的含义了。
然后就是查找操作。查找的时候我们需要同时试两个种类。维护答案的正确性。
针对于本题,我们需要维护三种关系,就是同类,吃,被吃。
这就要开三倍的并查集。
针对于每种关系,我们分为同类和不同类两种情况。
如果是同类,就到三个集合中分别合并。
如果不是同类,就1-3合并,2-1合并,3-2合并。
盗一张洛谷的图来解释:
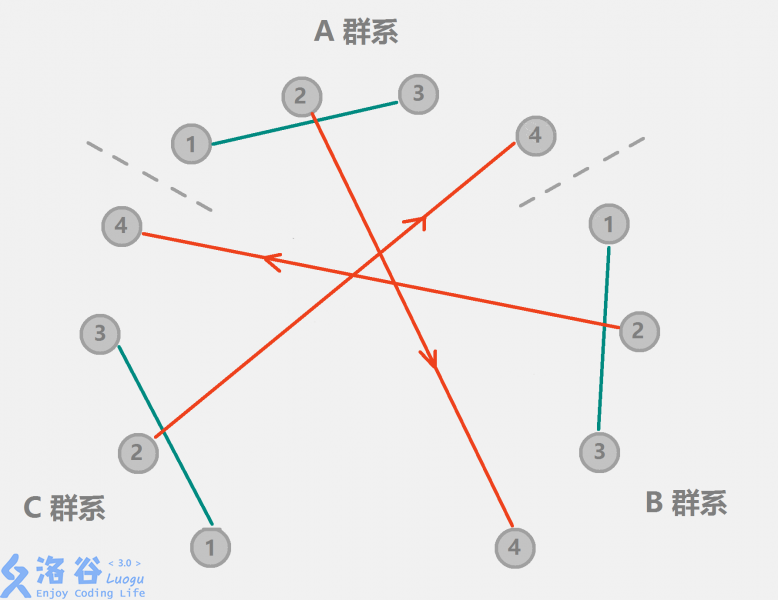
所以我们得出这样的代码:
#include<cstdio>
using namespace std;
int n,k,ans,fa[100001*3];
int find(int x)
{
if(fa[x]==x)
return x;
return fa[x]=find(fa[x]);
}
void unionn(int x,int y)
{
int fx=find(x);
int fy=find(y);
if(fx!=fy)
fa[fx]=fy;
}
int main()
{
scanf("%d%d",&n,&k);
for(int i=1;i<=3*n;i++)
fa[i]=i;
for(int i=1;i<=k;i++)
{
int asp,x,y;
scanf("%d%d%d",&asp,&x,&y);
if(x>n || y>n)
{
ans++;
continue;
}
if(asp==1)
{
if(find(x+n)==find(y) || find(x)==find(y+n))
ans++;
else
{
unionn(x,y);
unionn(x+n,y+n);
unionn(x+n+n,y+n+n);
}
}
else
{
if(find(x)==find(y) || find(x)==find(y+n))
ans++;
else
{
unionn(x,y+n+n);
unionn(x+n,y);
unionn(x+n+n,y+n);
}
}
}
printf("%d",ans);
return 0;
}
请大家好好理解。

