NOI 2016 区间
洛谷 P1712 [NOI2016]区间
题目描述
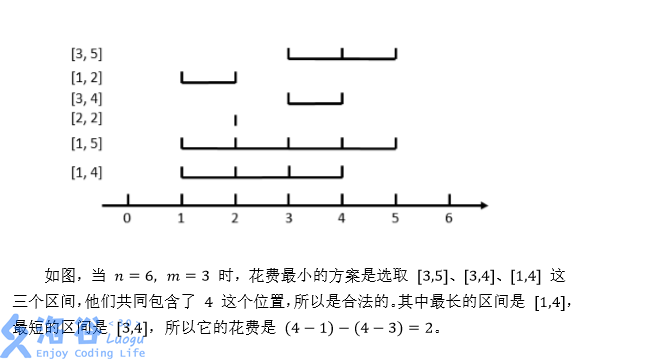
在数轴上有NN 个闭区间 [l_1,r_1],[l_2,r_2],...,[l_n,r_n][l1,r1],[l2,r2],...,[l**n,r**n] 。现在要从中选出MM 个区间,使得这MM 个区间共同包含至少一个位置。换句话说,就是使得存在一个 xx ,使得对于每一个被选中的区间[l_i,r_i][l**i,r**i] ,都有 l_i≤x≤r_il**i≤x≤r**i 。
对于一个合法的选取方案,它的花费为被选中的最长区间长度减去被选中的最短区间长度。区间[l_i,r_i][l**i,r**i] 的长度定义为r_i-l_ir**i−l**i ,即等于它的右端点的值减去左端点的值。
求所有合法方案中最小的花费。如果不存在合法的方案,输出-1−1 。
输入格式
第一行包含两个正整数N,MN,M 用空格隔开,意义如上文所述。保证1≤M≤N1≤M≤N
接下来NN 行,每行表示一个区间,包含用空格隔开的两个整数l_il**i 和r_ir**i 为该区间的左右端点。
N<=500000,M<=200000,0≤li≤ri≤10^9N<=500000,M<=200000,0≤l**i≤r**i≤109
输出格式
只有一行,包含一个正整数,即最小花费。
输入输出样例
输入 #1复制
输出 #1复制
说明/提示
题解:
(第二道紫题)
(开心)
这是一道线段树的题,加了一点点的尺取法思想(为此我特意学了尺取法)
所以我们得出这样的思路,先按照区间长度大小排序,进行离散化,按照我们排过序后的顺序依次加入区间,然后看一下是否有一个点的区间被覆盖的次数大于等于m,如果有的话,我们还需要统计最小长度,就尝试着把前面的内容依次删除,知道<m(临界点)。
其实这就是一个尺取法的过程。
通过上述的思路,我们发现这个思路代码实现上的难点一个是离散化,一个是尺取,还有一个就是如何统计得出有一个点的被覆盖次数比m大。
显然暴力枚举是不行的,所以我们考虑线段树维护这个覆盖次数。
所以就可以了。
代码大致如下:
#include<cstdio>
#include<algorithm>
#define lson pos<<1
#define rson pos<<1|1
using namespace std;
const int maxn=500001;
const int INF=1e9;
struct Point
{
int val,id;
}p[maxn<<2];
struct Data
{
int len,id;
}a[maxn<<2];
int L[maxn<<1],R[maxn<<1],n,m,maxr,cnt,num;
int tree[maxn<<3],add[maxn<<3];
bool cmp1(Point a,Point b)
{
return a.val<b.val;
}
bool cmp2(Data a,Data b)
{
return a.len<b.len;
}
void pushdown(int pos,int l,int r)
{
if(!add[pos])
return;
tree[lson]+=add[pos];
tree[rson]+=add[pos];
add[lson]+=add[pos];
add[rson]+=add[pos];
add[pos]=0;
return;
}
void fix(int pos,int l,int r,int x,int y,int val)
{
if(x>r||y<l)
return;
if(x<=l&&y>=r)
{
tree[pos]+=val;
add[pos]+=val;
return;
}
int mid=(l+r)/2;
pushdown(pos,l,r);
fix(lson,l,mid,x,y,val);
fix(rson,mid+1,r,x,y,val);
tree[pos]=max(tree[lson],tree[rson]);
return;
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
{
int u,v;
scanf("%d%d",&u,&v);
a[i].len=v-u;
a[i].id=i;
p[++cnt].val=u;
p[cnt].id=i;
p[++cnt].val=v;
p[cnt].id=i;
}
p[0].val=-1;
sort(p+1,p+cnt+1,cmp1);
for(int i=1;i<=cnt;i++)
{
if(p[i].val!=p[i-1].val)
num++;
int order=p[i].id;
if(!L[order])
L[order]=num;
else
R[order]=num;
}
maxr=num;
sort(a+1,a+n+1,cmp2);
int ans=INF,le=0,ri=0;
while(1)
{
while(tree[1]<m && ri<=n)
{
ri++;
int u=a[ri].id,v=L[u],w=R[u];
fix(1,1,maxr,v,w,1);
}
if(tree[1]<m)
break;
while(tree[1]>=m && le<=n)
{
le++;
int u=a[le].id,v=L[u],w=R[u];
fix(1,1,maxr,v,w,-1);
}
ans=min(ans,a[ri].len-a[le].len);
}
if(ans==INF)
printf("-1");
else
printf("%d",ans);
return 0;
}

