NOIP 2008 火柴棒等式
洛谷 P1149 火柴棒等式
JDOJ 1540: [NOIP2008]火柴棒等式 T2
Description
给你n根火柴棍,你可以拼出多少个形如“A+B=C”的等式?等式中的A、B、C是用火柴棍拼出的整数(若该数非零,则最高位不能是0)。用火柴棍拼数字0-9的拼法如图所示:
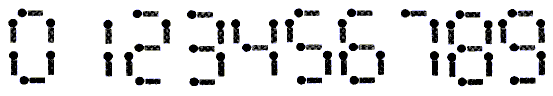
注意:
\1. 加号与等号各自需要两根火柴棍
\2. 如果A≠B,则A+B=C与B+A=C视为不同的等式(A、B、C> =0)
\3. n根火柴棍必须全部用上
Input
输入共一行,有一个整数n(n< =24)。
Output
输出共一行,表示能拼成的不同等式的数目。
Sample Input
Input 1: 14 Input 2: 18
Sample Output
Output 1: 2 Output 2: 9
HINT
【输入输出样例1解释】
2个等式为0+1=1和1+0=1。
【输入输出样例2解释】
9个等式为:
0+4=4
0+11=11
1+10=11
2+2=4
2+7=9
4+0=4
7+2=9
10+1=11
11+0=11
Source
题解:
因为n<=24,我们马上看出来,这个等式能模拟出的最大的数字绝对不会大于1000,所以我们考虑表示出1-1000的所有数字,基于这个开始枚举,最后得出答案。
是的,有些事情就是这么巧妙,什么打表啊,枚举啊,模拟啊,都是智慧的结晶,请大家不要嗤之以鼻——我19行结束的代码你用暴力搜索打了50多行,你凭什么嘲笑我??
所以我们开始模拟。
先处理出的a[]数组保存的是当数组下标为i的时候,需要几根火柴模拟出来。为什么a数组要开2000呢?因为后来判断的时候要a[i+j],而i和j都是1000规模的,不开2000会RE。
然后我们打表处理出m数组,表示拼出数字,注意是数字i的时候需要几根火柴,然后就可以按位表示了。应该很简单。
最后判断,不用多说了。
注意要加4.
所以AC了:
#include<cstdio>
using namespace std;
int n,ans;
int a[2001];
int m[]={6,2,5,5,4,5,6,3,7,6};
int main()
{
scanf("%d",&n);
a[0]=6;
for(int i=1;i<=2000;i++)
for(int j=i;j>=1;j/=10)
a[i]=a[i]+m[j%10];
for(int i=0;i<=1000;i++)
for(int j=0;j<=1000;j++)
if(a[i]+a[j]+a[i+j]+2+2==n)
ans++;
printf("%d",ans);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号