JDOJ 1927 求逆序对
洛谷 P1908 逆序对
JDOJ 1927: 求逆序对
题目描述
猫猫TOM和小老鼠JERRY最近又较量上了,但是毕竟都是成年人,他们已经不喜欢再玩那种你追我赶的游戏,现在他们喜欢玩统计。最近,TOM老猫查阅到一个人类称之为“逆序对”的东西,这东西是这样定义的:对于给定的一段正整数序列,逆序对就是序列中ai>aj且i<j的有序对。知道这概念后,他们就比赛谁先算出给定的一段正整数序列中逆序对的数目。
Update:数据已加强。
输入格式
第一行,一个数n,表示序列中有n个数。
第二行n个数,表示给定的序列。序列中每个数字不超过10^9109
输出格式
给定序列中逆序对的数目。
输入输出样例
输入 #1复制
输出 #1复制
说明/提示
对于25%的数据,n \leq 2500n≤2500
对于50%的数据,n \leq 4 \times 10^4n≤4×104。
对于所有数据,n \leq 5 \times 10^5n≤5×105
请使用较快的输入输出
应该不会n方过50万吧 by chen_zhe
题目略有不同,不影响双AC。
题解:
求逆序对我们一般使用归并排序,所谓归并排序,让我用一张图简单解释一下:
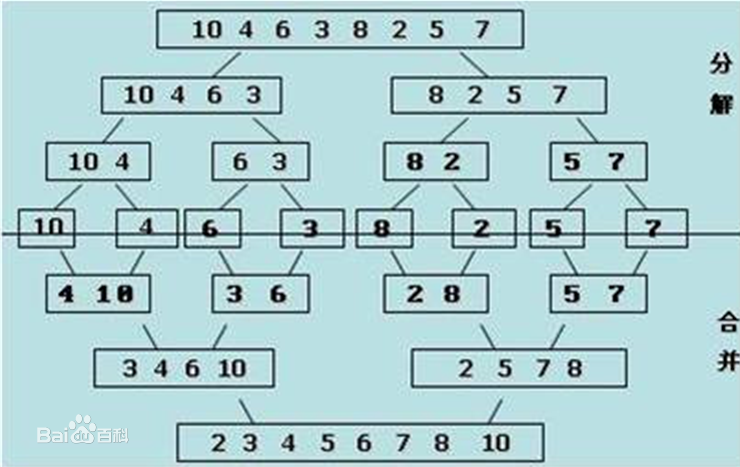
通过从百度百科上扒下来的这个图,我们可以发现归并排序其实是分治算法的一个简单应用。
归并归并,顾名思义,先分再并,针对一个无序序列,通过把元素分解之后交换顺序,最后合并出一个有序序列。
针对于求逆序对个数的问题,我们很容易得出,逆序对的个数就是归并排序过程中交换的次数。
请好好理解。
然后我们来看一看用树状数组如何实现求逆序对个数的题目。
方法1,传统方法,向下查询,向上修改。
这个方法需要逆向枚举每一个数,先查询一下已经插入的树状数组中比其小的元素个数,再累加ans。
然后先累加,再把它放到树状数组里。
方法2,向上查询,向下修改。
其实就是反过来。
正向枚举,先向上查询,根据树状数组的结构可以得出,查询到的结果就是已经插入到树状数组的比当前值大的元素的个数,累加ans即可。
但是在这里,为了满足洛谷的坑比需求,我采用了结构体排序加树状数组的一个方法。
详见代码。
#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
int c[500010],rk[500010],n;
long long ans;
struct point
{
int num,val;
}a[500010];
inline bool cmp(point q,point w)
{
if(q.val==w.val)
return q.num<w.num;
return q.val<w.val;
}
inline void fix(int p,int d)
{
for(;p<=n;p+=p&-p)
c[p]+=d;
}
inline int getsum(int x)
{
int sum=0;
for(;x;x-=x&-x)
sum+=c[x];
return sum;
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
scanf("%d",&a[i].val),a[i].num=i;
sort(a+1,a+1+n,cmp);
for(int i=1;i<=n;i++)
rk[a[i].num]=i;
for(int i=1;i<=n;i++)
{
fix(rk[i],1);
ans+=i-getsum(rk[i]);
}
printf("%lld",ans);
return 0;
}


