树状数组知识点详解
树状数组
树状数组是一种数据结构,它的作用就是优化查询和修改的操作。试想,我们假如在做一道题的时候使用裸的一维数组来存储数据,那每次区间修改需要O(1)的时间,但查询却需要O(n)的时间,针对于某些题目,数据量奇大无比,必然会TLE。所以我们使用树状数组来优化这两个操作,使得修改和查询均可以在O(logn)的时间内完成,提升效率。
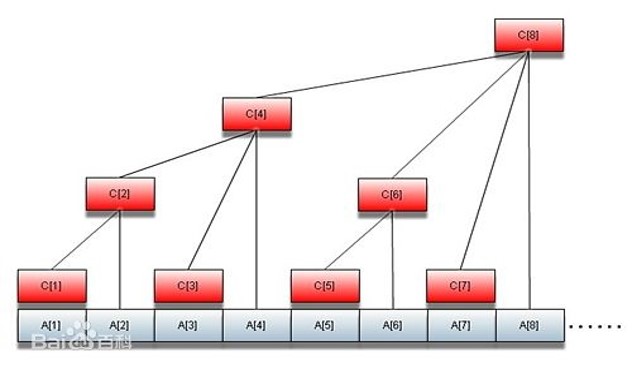
(这是百度百科上树状数组的图)
可以直观地看出树状数组是个什么模式,是的,这就是一棵树,而这棵树上每个节点存储的数据就是它所有儿子节点的数据和。所以我们就可以在树上做修改和区间查询(节点减节点),来做到树状数组这种优化方式。
树状数组的实现需要三个特别重要的函数,我一般把它们写成fix()(向上修改),getsum()(向下查询),和lowbit()(这个函数是理解树状数组运行过程的关键)。
lowbit()函数
首先从最关键的lowbit函数入手。
它长这个样子:
int lowbit(int x)
{
return x+=x&-x;
}
这里还涉及到了位运算的相关知识,所谓x&-x,是在二进制上的运算操作,它的实现也很简单,把x按位取反,最后同时上移最后的那个1。比如lowbit(34)最终的结果就是36。那么这个lowbit函数是干什么用的呢?
关于lowbit运算,有不太了解的小伙伴可以参考本蒟蒻的这篇博客:
我们可以把它理解成对树状数组的遍历方式。
根据树状数组的示意图可以发现,我们如果想对原数组进行元素修改,会牵连到于之关联的树状数组整个链。所以我们必须层层向上修改,每一层都要修改,才能保证树状数组存储的元素的正确性。
那么这个层层向上(向下),就需要lowbit这个函数,或者是说这个功能,来实现。
fix()函数
void fix(int x)
{
for(int i=x;i<=n;i+=i&-i)
c[i]++;
}
void fix(int x,int y)//表示在x元素处修改y个单位
{
for(int i=x;i<=n;i+=i&i)
c[i]+=y;
}
通过刚才学习lowbit函数,我们应该可以理解这个循环的含义。
其实就是层层向上修改树状数组的对应元素。
getsum()函数
int getsum(int x)
{
int ret=0;
for(int i=x;i;i-=i&-i)
ret+=c[i];
return ret;
}
这里注意,查询的时候要从上往下查询,这里默认查询的区间是1-->x,如果不是1到x,需要另外加参数。
树状数组的相关知识就介绍到这里,小伙伴们可以参考我树状数组的博客来进行例题训练。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号