NOIP 2000 方格取数
洛谷 P1004 方格取数
https://www.luogu.org/problemnew/show/P1004
JDOJ 2791: [NOIP2000]方格取数 T4
https://neooj.com:8082/oldoj/problem.php?id=2791
题目描述
设有N*N的方格图(N<=10,我们将其中的某些方格中填入正整数,而其他的方格中则放入数字0。如下图所示(见样例):
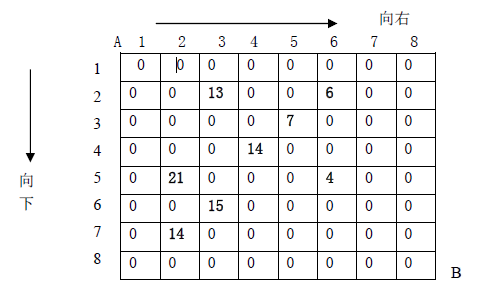

某人从图的左上角的A 点出发,可以向下行走,也可以向右走,直到到达右下角的B点。在走过的路上,他可以取走方格中的数(取走后的方格中将变为数字0)。
此人从A点到B 点共走两次,试找出2条这样的路径,使得取得的数之和为最大。
输入
输入的第一行为一个整数N(表示N*N的方格图),接下来的每行有三个整数,前两个表示位置,第三个数为该位置上所放的数。一行单独的0表示输入结束。
输出
只需输出一个整数,表示2条路径上取得的最大的和。
样例输入
8 2 3 13 2 6 6 3 5 7 4 4 14 5 2 21 5 6 4 6 3 15 7 2 14 0 0 0
样例输出
67
一开始的思路:
先跑一遍动归,一边跑一边记录路径,然后存下f[n][n],再加判断接着跑一遍,累加ans即可。
一遍写代码还一边嘲笑这道题水到爆炸的数据量。
直到卡在路径记录上。
后来发现动态规划的特点就是无后效性,每一个决策都是当前状态下的最优解,那么你想在f[n][n]状态下回溯记录路径......
再在原模板下加个深搜?
好像不科学。
于是我想了想,发现可以开四维数组,四重循环,也绝对不会爆炸。
越想越兴奋,真的像是找到了正解(事实证明的确是)
然后剩下的事就好办了。
这里要注意特判一下i=k && j=l的情况。
AC CODE:
#include<cstdio> #include<algorithm> using namespace std; int n; int map[11][11]; int f[11][11][11][11]; int main() { scanf("%d",&n); while(1) { int x,y,z; scanf("%d%d%d",&x,&y,&z); if(x==0 && y==0 && z==0) break; map[x][y]=z; } for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) for(int k=1;k<=n;k++) for(int l=1;l<=n;l++) { f[i][j][k][l]=max(f[i-1][j][k-1][l],max(f[i][j-1][k-1][l],max(f[i-1][j][k][l-1],f[i][j-1][k][l-1])))+map[i][j]+map[k][l]; if(i==k && j==l) f[i][j][k][l]-=map[i][j]; } printf("%d",f[n][n][n][n]); return 0; }

