POJ 1330 Nearest Common Ancestors
Nearest Common Ancestors
http://poj.org/problem?id=1330
Description
A rooted tree is a well-known data structure in computer science and engineering. An example is shown below:
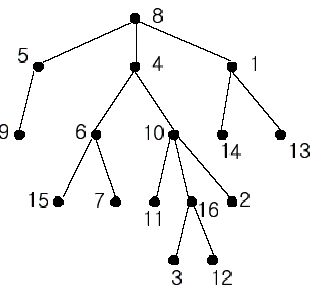
In the figure, each node is labeled with an integer from {1, 2,...,16}. Node 8 is the root of the tree. Node x is an ancestor of node y if node x is in the path between the root and node y. For example, node 4 is an ancestor of node 16. Node 10 is also an ancestor of node 16. As a matter of fact, nodes 8, 4, 10, and 16 are the ancestors of node 16. Remember that a node is an ancestor of itself. Nodes 8, 4, 6, and 7 are the ancestors of node 7. A node x is called a common ancestor of two different nodes y and z if node x is an ancestor of node y and an ancestor of node z. Thus, nodes 8 and 4 are the common ancestors of nodes 16 and 7. A node x is called the nearest common ancestor of nodes y and z if x is a common ancestor of y and z and nearest to y and z among their common ancestors. Hence, the nearest common ancestor of nodes 16 and 7 is node 4. Node 4 is nearer to nodes 16 and 7 than node 8 is.
For other examples, the nearest common ancestor of nodes 2 and 3 is node 10, the nearest common ancestor of nodes 6 and 13 is node 8, and the nearest common ancestor of nodes 4 and 12 is node 4. In the last example, if y is an ancestor of z, then the nearest common ancestor of y and z is y.
Write a program that finds the nearest common ancestor of two distinct nodes in a tree.

In the figure, each node is labeled with an integer from {1, 2,...,16}. Node 8 is the root of the tree. Node x is an ancestor of node y if node x is in the path between the root and node y. For example, node 4 is an ancestor of node 16. Node 10 is also an ancestor of node 16. As a matter of fact, nodes 8, 4, 10, and 16 are the ancestors of node 16. Remember that a node is an ancestor of itself. Nodes 8, 4, 6, and 7 are the ancestors of node 7. A node x is called a common ancestor of two different nodes y and z if node x is an ancestor of node y and an ancestor of node z. Thus, nodes 8 and 4 are the common ancestors of nodes 16 and 7. A node x is called the nearest common ancestor of nodes y and z if x is a common ancestor of y and z and nearest to y and z among their common ancestors. Hence, the nearest common ancestor of nodes 16 and 7 is node 4. Node 4 is nearer to nodes 16 and 7 than node 8 is.
For other examples, the nearest common ancestor of nodes 2 and 3 is node 10, the nearest common ancestor of nodes 6 and 13 is node 8, and the nearest common ancestor of nodes 4 and 12 is node 4. In the last example, if y is an ancestor of z, then the nearest common ancestor of y and z is y.
Write a program that finds the nearest common ancestor of two distinct nodes in a tree.
Input
The input consists of T test cases. The number of test cases (T) is given in the first line of the input file. Each test case starts with a line containing an integer N , the number of nodes in a tree, 2<=N<=10,000. The nodes are labeled with integers 1, 2,..., N. Each of the next N -1 lines contains a pair of integers that represent an edge --the first integer is the parent node of the second integer. Note that a tree with N nodes has exactly N - 1 edges. The last line of each test case contains two distinct integers whose nearest common ancestor is to be computed.
Output
Print exactly one line for each test case. The line should contain the integer that is the nearest common ancestor.
Sample Input
2 16 1 14 8 5 10 16 5 9 4 6 8 4 4 10 1 13 6 15 10 11 6 7 10 2 16 3 8 1 16 12 16 7 5 2 3 3 4 3 1 1 5 3 5
Sample Output
4 3
看到大佬们用的都是离线tarjan,然而我并不会(逃
所以我用的是朴素LCA算法,深搜加LCA;
俗称爬一爬。一层一层往上爬,没有倍增,慢到爆炸。
然而确实很好用(P)
代码:
#include <iostream> #include <cstdio> #include <cstring> #include <algorithm> using namespace std; int t,n; int tot,to[10001],nxt[10001],head[10001]; int fa[10001],deep[10001]; void add(int x,int y) { to[++tot]=y; nxt[tot]=head[x]; head[x]=tot; } void dfs(int x,int step) { deep[x]=step; for(int i=head[x];i;i=nxt[i]) dfs(to[i],step+1); } int lca(int x,int y) { if(deep[x]<deep[y]) swap(x,y); while(deep[x]>deep[y]) x=fa[x]; while(x!=y) x=fa[x],y=fa[y]; return x; } int main() { scanf("%d",&t); for(int k=1;k<=t;k++) { int root; memset(head,0,sizeof(head)); tot=0; scanf("%d",&n); for(int i=1;i<n;i++) { int a,b; scanf("%d%d",&a,&b); add(a,b); fa[b]=a; } for(int i=1;i<=n;i++) if(!fa[i]) root=i; int x,y; scanf("%d%d",&x,&y); dfs(root,1); printf("%d\n",lca(x,y)); } return 0; }
//一群大佬给我调的。
这里要着重注意一下,本题的根节点是不确定的,所以要额外加一个变量root来记录根节点是哪,然后才可以递归深搜,最后用爬一爬出解。

