word2vec

word2vec

word2vec是Google在2013年推出的一个工具。word2vec通过训练，可以将所有的词向量化，这样就可以定量的去度量词与词之间的关系，挖掘词之间的联系；同时还可以将词向量输入到各种RNN网络中进一步处理。因此，word2vec 输出的词向量可以被用来做很多自然语言处理相关的工作，比如聚类、找同义词、词性分析等等、文本分析等，是自然语言处理的重要基础。

本文希望能带你快速入门word2vec。

paper link

Efficient Estimation of Word Representations in Vector Space

word2vec Parameter Learning Explained

基本概念扫盲

语料库(corpus)、词(word)、词汇表(vocabulary)

语料库一般是指一些根据研究需要从自网站、新闻、报纸等采集的大规模文本。而“词”是语料中的最小单位。例如：

Winners do what losers do not want to do.

在处理这段非常简单的语料中，我们会把"winners"作为一个完整词处理，而不会把词分为字符单独处理。通常在自然语言处理(NLP)中，词也是最小单位，所以有“词向量”，但是没有“字符向量“。

而统计语料中出现的不重复的词构成即可构成词汇表。如上段语料中出现了"winners losers what want do not to"这7个词，其中do出现了3次。

为什么要进行词嵌入(word embedding)？

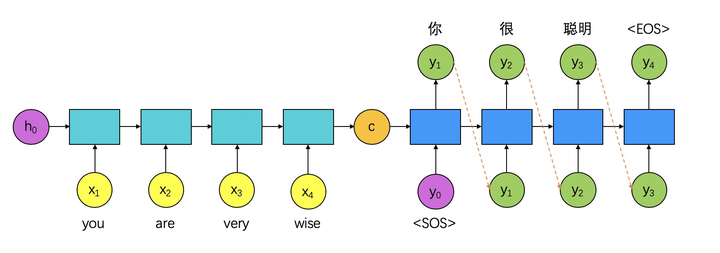
以机器翻译为例，要把"you"输入到RNN网络中，必须把单词转化为一个向量（即把词“嵌入”到高维空间）。

\[you\Longleftrightarrow V_{you}=[v_1,v_2,...,v_n] \]

那么最简单粗暴的词嵌入方法就是one-hot编码：

\[\begin{matrix}I&\Longleftrightarrow& V_I&=&[1,0,0,0,0,0,0,...,0]\\you&\Longleftrightarrow& V_{you}&=&[0,1,0,0,0,0,0,...,0]\\is&\Longleftrightarrow& V_{is}&=&[0,0,1,0,0,0,0,...,0]\\are&\Longleftrightarrow& V_{are}&=&[0,0,0,1,0,0,0,...,0]\\very&\Longleftrightarrow& V_{very}&=&[0,0,0,0,1,0,0,...,0]\\wise&\Longleftrightarrow& V_{wise}&=&[0,0,0,0,0,1,0,...,0]\\smart&\Longleftrightarrow& V_{smart}&=&[0,0,0,0,0,0,1,...,0]\end{matrix} \]

那么one-hot编码有什么缺点呢？

• 维度灾难

  一般情况下，常用英语单词约8000个，如果使用one-hot编码，每个词向量就是8000维；对应的如果有100000个词，那么每个词向量就是100000维。在实际应用中，词向量维度太大，会造成网络参数量大、网络推理速度慢、网络运行占用内存高等问题。

• 编码过于稀疏

  在one-hot编码的词向量中，数值几乎全部是0，非常稀疏，很可能导致实际中网络难以收敛。

• 无法表示词间的关系

  有向量\(A=(a_1,a_2,...,a_n)\)和\(B=(b_1,b_2,...,b_n)\)，定义\(A\)和\(B\)之间相似度为

  \[similarity=cos(\theta)=\frac{A\cdot B}{\left \| A \right \| \left \| B \right \|}=\frac{\sum^n_{i=1}a_i\cdot b_i}{\sqrt{\sum^n_{i=1}(a_i)^2}\sqrt{\sum^n_{i=1}(b_i)^2}} \]

  对于one-hot编码，任意两个词间的相似度都为0，这是违背实际情况的。

那么实际情况是什么？举例说明：词"cars"是"car"的复数形式，词"trucks"又是"truck"的复数形式，所以实际中我们希望他们词向量相似度很大：

\[similarity(V_{car},V_{cars})\approx similarity(V_{truck},V_{trucks})\approx 1 \]

由于"car"和"truck"词义接近，"car"和"china"词义差别较大，我们也希望有如下关系：

\[similarity(V_{car},V_{truck})> similarity(V_{car},V_{china}) \]

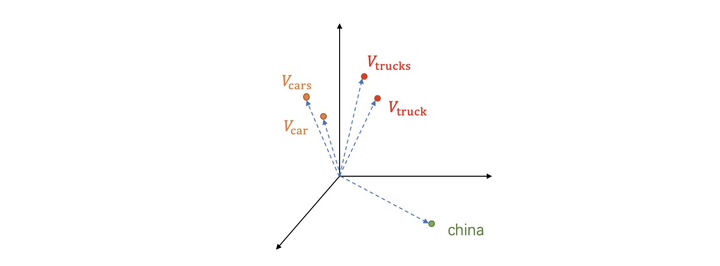
那么不禁要问：有没有一种神经网络，输入每个词的one-hot编码，就可以输出符合上述要求的词向量？

有，就是word2vec！

word2vec详解

word2vec是一个典型的3层全连接网络：INPUT->PROJECTION->OUTPUT，假设：

• INPUT层->PROJECTION层权重为\(W_1\)矩阵
• PROJECTION层->OUTPUT层权重为\(W_2\)矩阵

其中\(W_1,W_2\)通过训练得到

flowchart LR word-->1[one-hot label]-->INPUT--W1-->PROJECTION--W2-->OUTPUT-->2[word vector] INPUT-->PROJECTION INPUT-->PROJECTION INPUT-->PROJECTION INPUT-->PROJECTION INPUT-->PROJECTION INPUT-->PROJECTION INPUT-->PROJECTION INPUT-->PROJECTION PROJECTION-->OUTPUT PROJECTION-->OUTPUT PROJECTION-->OUTPUT PROJECTION-->OUTPUT PROJECTION-->OUTPUT PROJECTION-->OUTPUT PROJECTION-->OUTPUT PROJECTION-->OUTPUT

那么：\(词向量 = 词的one-hot编码向量（转置）\times W_1\)

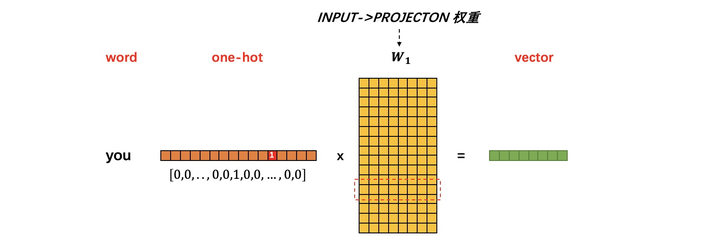
所以\(W_1\)就是由字典中所有词对应的词向量组成的矩阵：

\[W_1=(V^T_{word_1},V^T_{word_2},...,V^T_{word_n}) \]

那么如何训练网络获得\(W_1,W_2\)矩阵？

word2vec提出了CBOW与skip-gram结构。

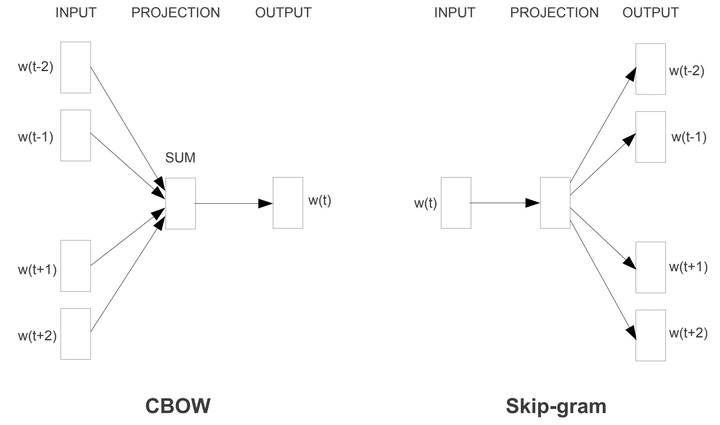
CBOW结构：根据输入周围\(2c\)个词来预测出这个词本身（即通过上下文预测词语)：

\[CBOW:context(w_t)=(w_{t-c},...,w_{t-1},w_{t+1},...,w_{t+c})\overset{predict}{\longrightarrow}w_t \]

skip-gram结构：根据输入词来预测周围\(2n\)个词（即预测词语的上下文)：

\[skip-gram:w_t \overset{predict}{\longrightarrow}context(w_t)=(w_{t-c},...,w_{t-1},w_{t+1},...,w_{t+c}) \]

huffman树

huffman树是一种特殊结构的二叉树，通过huffman树编码的huffman码，在通信领域有着广泛的应用。在word2vec模型中构建PROJECTION->OUTPUT的Hierarchical softmax过程中，也使用到了huffman树。

构建huffman树流程：

1. 根据给定的n个权值{w1, w2, w3 ... wn}，构造n棵只有根节点的二叉树，令起权值为wj

2. 在森林中选取两棵根节点权值最小的树作为左右子树，构造一颗新的二叉树，置新二叉树根节点权值为其左右子树根节点权值之和。

   注意，左子树的权值应小于右子树的权值。

3. 从森林中删除这两棵树，同时将新得到的二叉树加入森林中。

   换句话说，之前的2棵最小的根节点已经被合并成一个新的结点了。

4. 重复上述两步，直到只含一棵树为止，这棵树即是“哈弗曼树”

接下来举例说明如何构造huffman树:

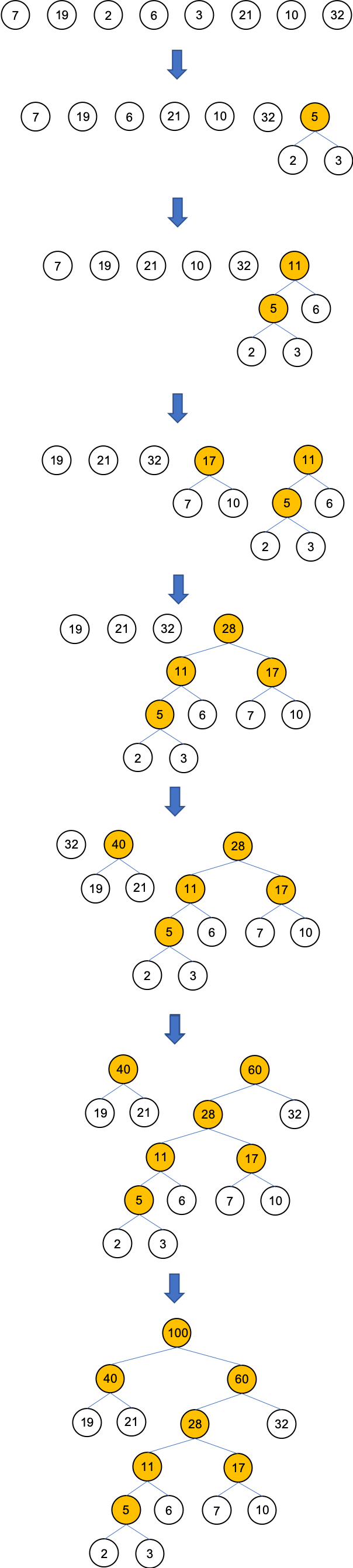
假设我们从某书籍中收集了一段语料，统计在语料中出现的词及每个词出现的次数，生成如下词汇表（这里只是举例，现实中的词汇表一定会非常大）。

vocabulary = {
    "are" 32,
    "you": 21,
    "and": 19,
    "very": 10,
    "hi": 7,
    "guys": 6,
    "wise": 2,
    "smart": 3,
}

然后通过每个词在语料中的出现次数建立huffman树，作为PROJECTION->OUTPUT结构。

另外在word2vec中约定：从huffman树根节点(root)开始，每次父节点向左子叶遍历编码为1，向右子叶遍历为0。如and编码为11，smart编码为01110（出现频率越高的词编码越短）。

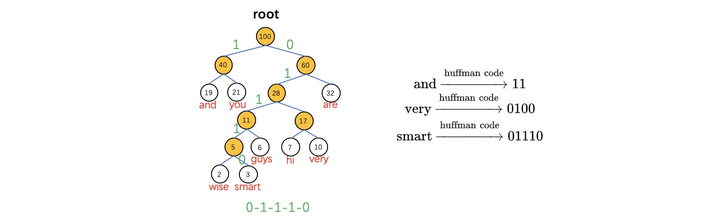
在word2vec中使用huffman树的重要原因就是降低训练时的计算量。

一般来说，训练用的语料库都非常大。而在语料库中，有一些词出现频率很高，还有一些词出现频率很低，而且这种频率差异是非常巨大的。那么采用huffman树后，出现频率很高的常用词路径短，计算量小，从而降低了整个word2vec模型在训练时的计算开销。

CBOW(Continuous Bag of Words)结构

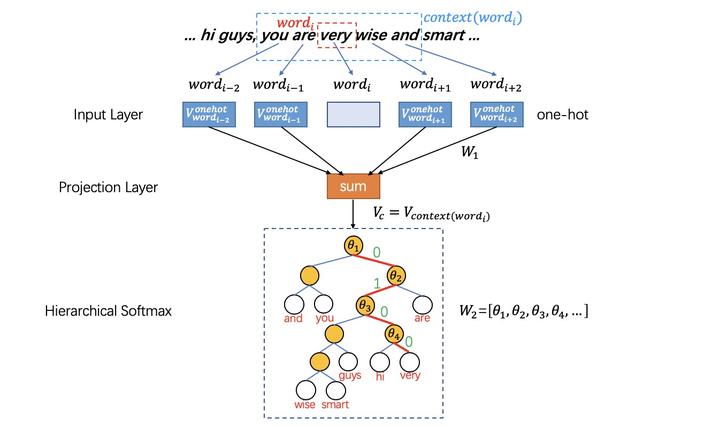
在之前提到过，CBOW根据输入词周围\(2c\)个词来预测出这个词本身。如果当前网络已经充分训练，那么输入you、are、 wise、and四个词，则应该输出词very。那么CBOW结构的word2vec网络是如何训练的？

• 从INPUT->PROJECTION层

  CBOW结构首先会取中心词的\(2c\)个上下文词，然后用这些上下文词的one-hot编码向量乘以\(W_1\)权重再求和：

  \[V_{context(word_i)}=V_c=\frac{1}{2c}(\sum^c_{t=1}V_{onehot(word_{i+t})}\cdot W_1+\sum^c_{t=1}V_{onehot(word_{i-t})}\cdot W_1) \]

  其中\(V_{onehot(word_i)}\)代表词\(word_i\)的one-hot编码向量；\(V_{context(word_i)}\)代表\(word_i\)的上下文词的词向量之和（为了便于书写记为\(V_c\)）

• 从PROJECTION->OUTPUT层(Hierarchical Softmax)

  以词"very"为例在huffman树中需要分类4次（编码为0100）

  • 第一次分类结果\(d_1=0\)概率为：

    \[P(d_1|V_c,\theta_1)=1-\sigma(V^T_c\cdot \theta_1) \]

    其中\(\sigma(x)=\frac{1}{1+e^x}\in(0,1)\)

    

  • 第二次分类为\(d_2=1\)概率为：

    \[P(d_2|V_c,\theta_2)=\sigma(V^T_c\cdot \theta_2) \]

  • 第三次分类为\(d_3=0\)概率为：

    \[P(d_3|V_c,\theta_3)=1-\sigma(V^T_c\cdot \theta_3) \]

  • 第四次分类为\(d_4=0\)概率为：

    \[P(d_4|V_c,\theta_4)=1-\sigma(V^T_c\cdot \theta_4) \]

  所以词"very"最终Hierarchical Softmax最终概率为：

  \[P(very|context(very))=\prod_{j=1}^{4}P(d_j|V_c,\theta_j) \]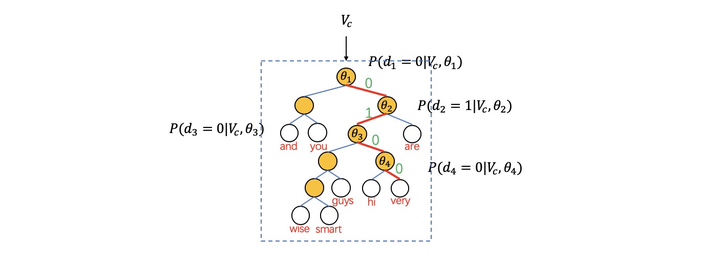

  

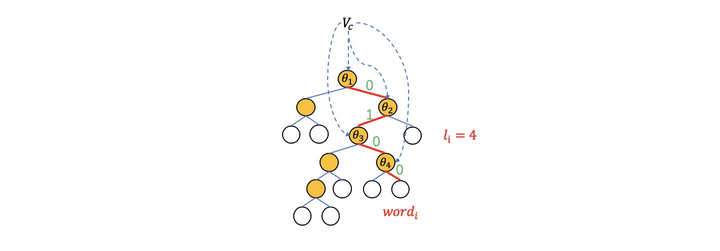
  推广一下，词\(word_i\)最终Hierarchical Softmax最终概率为:

  \[P(word_i|context(word_i))=\prod_{j=1}^{l_i}P(d_j|V_c,\theta_j) \]

  其中\(l_i\)为\(word_i\)的huffman树路径长度（如"very"为4），而\(P(d_j|V_c,\theta_j)\)为：

  \[P(d_j|V_c,\theta_j)=\left\{\begin{matrix} \sigma(V_c^T\cdot \theta_j) &d_j=0 \\ 1-\sigma(V^T_c\cdot \theta_j)&d_j=1 \end{matrix}\right.\]

  简化一下

  \[P(d_j|V_c,\theta_j)=[\sigma(V_c^T\cdot \theta_j) ]^{1-d_j}\cdot[1-\sigma(V^T_c\cdot \theta_j)]^{d_j} \]

• 从OUTPUT->PROJECTION->INPUT训练

  在训练时，我们显然希望输入是\(word_i\)的\(2c\)个上下文词时输出使\(word_i\)，即概率\(P(word_i|context(word_i))\)越大越好，那么最终优化目标就是对预料中每个词\(word_i\)都有\(L\)最大：

  \[\begin{matrix}L&=\underset{word_i\in C}{\sum}P(word_i|context(word_i))\\&=\underset{word_i\in C}{\sum}\prod_{j=1}^{l_i}[\sigma(V_c^T\cdot \theta_j) ]^{1-d_j}\cdot[1-\sigma(V^T_c\cdot \theta_j)]^{d_j}\end{matrix} \]

  其中\(C\)代表训练使用的语料库，\(l_i\)代表词\(word_i\)的huffman树路径长度。而优化目标是乘法形式，所以取对数\(log\)将优化目标转化为加法：

  \[\begin{matrix}L'&=\underset{word_i\in C}{\sum}log\prod_{j=1}^{l_i}[\sigma(V_c^T\cdot \theta_j) ]^{1-d_j}\cdot[1-\sigma(V^T_c\cdot \theta_j)]^{d_j}\\&=\underset{word_i\in C}{\sum}\sum^{l_1}_{i=1}\{(1-d_j)log[\sigma(V_c^T\cdot \theta_j)]+g_jlog[1-\sigma(V_c^T\cdot \theta_j)]\}\end{matrix} \]

  由于优化目标是使\(L'\)最大，那么训练采用梯度上升算法，即每当获取新的训练中心词\(word_i\)时都会通过梯度更新一次权重。记：

  \[L'(i,j)=(1-d_j)log[\sigma(V_c^T\cdot \theta_j)]+g_jlog[1-\sigma(V_c^T\cdot \theta_j)] \]

  这里\(L'(i,j)\)时中心词为\(word_i\)时的优化目标，即希望通过调整\(\theta_j,V_c\)使得\(L'(i,j)\)最大，所以计算\(L'(i,j)\)对\(\theta_j\)的偏导数为

  \[\frac{\partial L'(i,j)}{\partial V_c}=[1-d_j-\sigma(V_c^T\cdot \theta_j)]\theta_j \]

  即可更新\(W_1\)中上下文词的词向量\(V_{word_n}\)（注意这里的\(word_n\in context(word_i)\)）

  \[V^{new}_{word_i}=V^{old}_{word_n}+\eta\sum^{l_i}_{j=1}\frac{\partial L'(i,j)}{\partial V_c} \]

  其中\(\eta\)表示梯度上升学习率

  对于上式一个比较通俗且不严谨的理解：

  误差传给了谁，谁就会把梯度返回给传它误差的节点，即“原路送回“。在前传中通过\(V_c\)点将误差传递给了后续网络，那么在反传中后续网络也要把自己所有的梯度\(\sum^{l_i}_{j=1}\frac{\partial L'(i,j)}{\partial V_c}\)还给\(V_c\)节点，然后\(V_c\)又会把梯度返还给\(2c\)个上下文词的词向量。

  

skip-gram结构

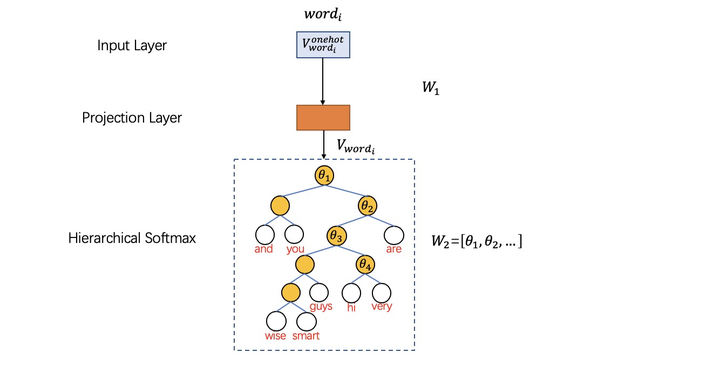
在之前提到过，skip-gram根据输入词词来预测出周围\(2c\)个上下文词。如果当前网络已经充分训练，那么输入very，则应该输出you、are、 wise、and四个上下文词。

从INPUT->PROJECTION计算\(word_i\)的词向量\(V_{worad_i}\)，然后PROJECTION直接向后续分层softmax输出\(V_{worad_i}\) （CBOW是求和）。skip-gram的优化目标与CBOW稍微不同：

\[L'=\underset{word_i\in C}{\sum}log \underset{u\in context(word_i)}{\prod} \prod^{l_i}_{j=1}[\sigma(V_c^T\cdot \theta_j) ]^{1-d_j}\cdot[1-\sigma(V^T_c\cdot \theta_j)]^{d_j} \]

其中多出的\(\underset{u\in context(word_i)}{\prod}\)符号代表skip-gram要通过\(2c\)个huffman树分别输出\(2c\)个上下文词，\(\theta^u_j\)中的\(u\)代表每个输出词对应的\(\theta_j\)参数。skip-gram与CBOW非常接近，考虑篇幅这里不再介绍。

word2vec实际测试

Google提供了word2vec的c代码。使用代码和text8语料库训练200维词向量，可以看到与词"google"余弦下降速度最大的词依次是"yahoo"和"gmail"。Amazing！

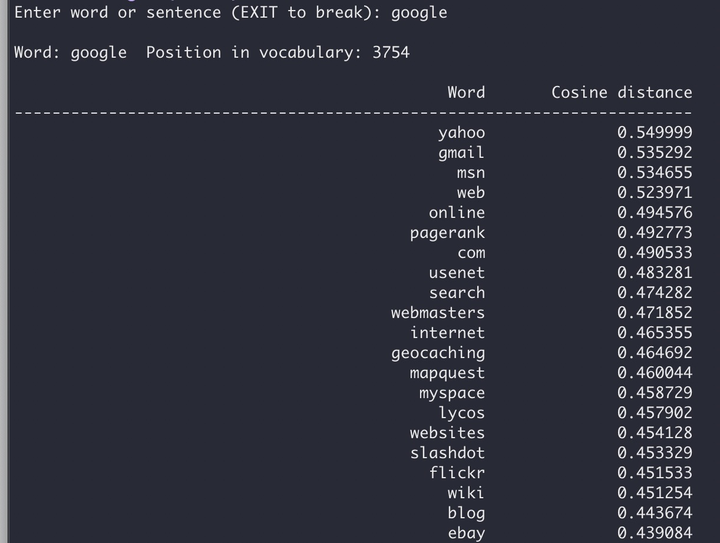
word2vec缺点

• OOV(Out of vocabulary)

在word2vec中，词汇表从开始训练就已经是确定的。那么在使用时，必然会有词不在词汇表中。一般使用<UNKNOW>特殊标志符解决OOV问题，但是当句子中<UNKNOW>过多时必然严重影响精度。

后续ELMO使用char cnn、Bert使用word piece，基本解决了OOV问题。

• 无法处理多义词

很多词在不同语境是有含义不同，即多义词。而word2vec中所有词的embeding向量都是训练好即固定的，无法在使用时根据上下文调整，导致处理多义词效果差。

ELMO和Bert使用训练language model，动态生成embeding向量，解决多义词问题。