Few-shot Learning
Few-shot Learning
问题定义
Few-shot Learning 是 Meta Learning 在监督学习领域的应用。Meta Learning,又称为learning to learn,该算法旨在让模型学会“学习”,能够处理类型相似的任务,而不是只会单一的分类任务。举例来说,对于一个LOL玩家,他可以很快适应王者荣耀的操作,并在熟悉后打出不错的战绩。人类利用已经学会的东西,可以更快的掌握一些新事物,而传统的机器学习方法在这方面的能力还有所欠缺,因此提出了元学习这个概念。
Meta learning 中,在 meta training 阶段将数据集分解为不同的 meta task,去学习类别变化的情况下模型的泛化能力,在 meta testing 阶段,面对全新的类别,不需要变动已有的模型,就可以完成分类。
在 few-shot learning 中有一个术语叫做 \(N-way\ K -shot\) 问题。形式化来说,few-shot 的训练集中包含了很多的类别,每个类别中有多个样本。在训练阶段,会在训练集中随机抽取 N 个类别,每个类别 \(K\) 个样本(总共 \(N*K\) 个数据),构建一个 meta-task,作为模型的支撑集(support set)输入;再从这 \(N\) 个类中剩余的数据中抽取一批(batch)样本作为模型的预测对象(batch set)。即要求模型从 \(N*K\) 个数据中学会如何区分这 \(N\) 个类别,这样的任务被称为 \(N-way\ K-shot\) 问题。
那这个小型分类任务的训练集和测试集具体是怎么划分的呢?
以5-Way 5-Shot分类问题为例,在构建一个任务的数据集时的具体流程应该如下:
-
从元数据集(Meta-dataset)中随机抽取5类(way)样本,每一类样本随机抽取5+1个(shot)实例
元数据集:就是指整体数据集中可以理解为传统的大型数据集,其中数据类别>>N-Way,每一类的实例数量>>K-Shot
-
从这5类样本的6个实例中,每类样本随机抽取5个实例一起作为Training Set(→
Support Set),每一类剩下的一个实例一起组成Testing Set(→Query Set)- 由于元学习是以任务(Task)作为自己的训练数据的,即元学习的实际训练集和测试集是由一个个的Task组成的,所以为了进行区分,每个任务内部的训练集(Training Set)更名为支持集(Support Set)、测试集更名为查询集(Query Set)
-
训练:从Support Set中每一类随机选取一个实例,一起够成一组训练数据,输入到模型中,进行训练
-
测试:从Query Set中随机抽取一个实例,用模型判断其属于哪一类
这个判断过程其实可以视为一种查询过程,给定了支持集,只要让模型能够准确的查询到其属于支持集中的哪一类即可证明模型性能较好
-
重复几轮,最终得出该任务模型的准确率,实际上即是
元学习参数确定的模型在该任务上的损失 -
损失梯度反向传播到元学习参数,对其进行更新,也即元学习过程
| way 1 (c1) | way 2 (c2) | way 3 (c3) | way 4 (c4) | way 5 (c5) | |
|---|---|---|---|---|---|
| \(c_{11}\) | \(c_{21}\) | \(c_{31}\) | \(c_{41}\) | \(c_{51}\) | Support |
| \(c_{12}\) | \(c_{22}\) | \(c_{32}\) | \(c_{42}\) | \(c_{52}\) | Support |
| \(c_{13}\) | \(c_{23}\) | \(c_{33}\) | \(c_{43}\) | \(c_{53}\) | Support |
| \(c_{14}\) | \(c_{24}\) | \(c_{34}\) | \(c_{44}\) | \(c_{54}\) | Support |
| \(c_{15}\) | \(c_{25}\) | \(c_{35}\) | \(c_{45}\) | \(c_{55}\) | Support |
| \(c_{16}\) | \(c_{26}\) | \(c_{36}\) | \(c_{46}\) | \(c_{56}\) | Query |
Meta learning
在进一步了解小样本学习前,先得了解元学习的相关内容。
元学习的核心想法是先学习一个先验知识(prior),这个先验知识对解决 few-shot learning 问题特别有帮助。Meta-learning 中有 task 的概念,比如上面图片讲的 5-way 1-shot 问题就是一个 task,我们需要先学习很多很多这样的 task,然后再来解决这个新的 task 。重要的一点,这是一个新的 task。分类问题中,这个新的 task 中的类别是之前我们学习过的 task 中没有见过的! 在 Meta-learning 中之前学习的 task 我们称为 meta-training task,我们遇到的新的 task 称为 meta-testing task。因为每一个 task 都有自己的训练集和测试集,因此为了不引起混淆,我们把 task 内部的训练集和测试集一般称为 support set 和 query set
Meta-learning 方法的分类标准有很多,为解决过拟合问题,有下面常见的3种方法
- 学习微调 (Learning to Fine-Tune)
- 基于 RNN 的记忆 (RNN Memory Based)
- 度量学习 (Metric Learning)
论文解读——Model-Agnostic Meta-Learning for Fast Adaptation of Deep Networks
元学习的目标是在各种学习任务上训练一个可以仅仅使用少量训练样本就可以解决新任务的模型,在本文中,模型的参数训练很明确,所以从新任务的少量样本做几步梯度下降就可以在新任务上得到好的泛化性。同时,由于模型可应用于一系列使用梯度下降训练的模型,包括分类,回归,强化学习等等,所以也叫作模型无关的模型。
本文的关键思想在于训练模型的初始参数,使得模型的参数在某个新任务上仅适用少量样本经过一步或者几步梯度下降更新后就可以早新任务上有很好的表现。从特征学习的角度来看,这是一个建立适应多种任务的内部特征表达的过程,使得其可以更容易,更快速的fine-tune;从动态系统的角度来看,学习过程可以被看做是最大化loss function对于和新任务有关的参数的敏感度,当敏感度高时,参数的小的局部改变可以使loss得到巨大的提高。
文章的title,其中有三个关键字Model-Agnostic(与模型无关的)、Fast Adaptation(快速适应)、Deep Networks,这三个关键字是文章的核心。
- Model-Agnostic
- task换成其他可以进行SGD过程的模型
- Deep Networks
- 适用于所有的深度学习模型
模型
考虑一个模型,用\(f(x)=a\)表示,我们需要训练这个网络使得它可以适应不同的无限的任务
在元学习过程中,模型被训练以适用于大量或无限任务。任务可以形式化地定义如下
其中\(\mathcal{L} ()\)是损失函数,这个损失是指在测试集上的损失,会在下面详细叙述。\(q()\)是样本的分布。由损失函数\(\mathcal{L}\),基于初始观察值的分布\(q(x_1)\),一个transition分布\(q(x_{t+1}∣x_t,a_t)\),eposide length \(H\)组成。
对于模型要适应的任务分布\(p(\)\(\mathcal{T})\) ,在K-shot learning的设定下,模型从\(p(\)\(\mathcal{T})\)采样任务\(\mathcal{T}_i\),再从\(q_i\)中采样\(K\)个样本,产生由\(\mathcal{T}\)产生的反馈\(\mathcal{L}_{\mathcal{T}_i}\) 。在\(K\)个样本上训练,然后在\(\mathcal{T}_i\)的新样本上进行测试。然后,通过考虑新样本的测试误差改变相应的参数以提升模型效果,实际上,在元学习过程中,这个测试误差被当做是训练误差。
算法
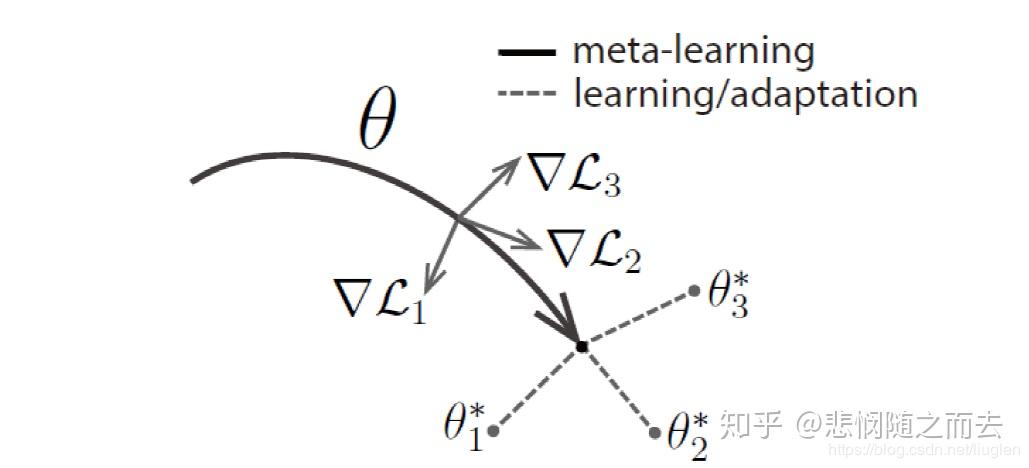
在学习过程中,一些特征比其他的更具有迁移性。比如,一个神经网络可能学到广泛适应于p(T)中所有任务内部特征,而不是对于某个单独的任务。为了提取这种更具有一般性的特征,在新任务上使用基于梯度下降的fine-tune的方式去训练模型。实际上,我们希望找到对于任务改变敏感的参数。
形式上,考虑参数为\(\theta\)的函数\(f_\theta\)表示的模型,当在新任务\(\mathcal{T}_i\)执行一步或者几步梯度下降后,模型的参数变成了\(\theta_{i}'\),当执行一步梯度更新时,\(\theta_{i}'=\theta-\alpha\bigtriangledown _{\theta}\mathcal{L}_{\mathcal{T}_i}(f_\theta)\)
模型的参数通过从与\(\theta\)对应的\(p(\mathcal{T})\)中采样的所有任务对应的\(f_{\theta_{i}'}\)进行优化,\(\underset{\theta}{min}\underset{\mathcal{L}_i\sim p(\mathcal{T})}{\sum}\mathcal{L}_{\mathcal{T}_i}(f_{\theta_{i}'})=\underset{\mathcal{L}_i\sim p(\mathcal{T})}{\sum}\mathcal{L}_{\mathcal{T}_i}(f_\theta-\alpha\bigtriangledown _{\theta}\mathcal{L}_{\mathcal{T}_i}(f_\theta))\)
需要注意的是元优化过程是针对模型参数\(\theta\)的,但是是通过更新后的参数\(\theta'\)计算的。在任务间的优化通过SGD,所以参数更新后,\(\theta \leftarrow \theta -\beta \bigtriangledown_{\theta}\underset{\mathcal{L}_i\sim p(\mathcal(T))}{\sum}\mathcal{L}_{\mathcal{T}_i}(f_{\theta_i'})\)
MAML的梯度计算包含二阶导数,计算时,需要额外的反向传播来计算海瑟矩阵。本文中,同时实验了不进行这次反向传播,使用一阶导近似的情况,最终准确度是差不多的。说明了MAML的大部分提升来自于基于任务目标优化得到的梯度,而不是通过梯度的二次微分。

分类或回归问题
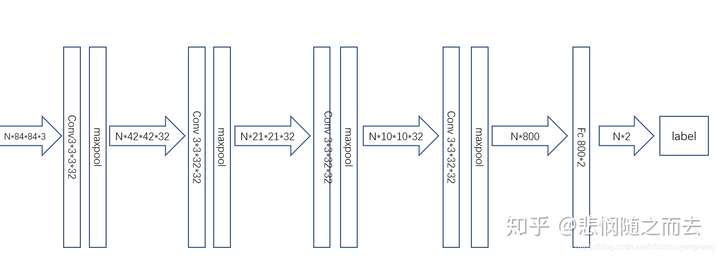
所谓的task在图片分类的这个实验中就是一个普通的卷积神经网络,当然作者实验中也提供了不是卷积神经网络的普通网络的版本。这个网络图如下:

- 对于分类问题,使用交叉熵损失函数
- 对于回归问题,使用MSE
其中\(p(\mathcal{T})\) 是Task的分布,其实在实现中并没有去特别的设定,个人觉得就是对样本采样的那一块就顺带形成了,只是不清楚是什么分布。\(\alpha,\beta\)分别是task中的进行梯度下降的学习率、和meta-learning过程的学习率,\(\theta\)是模型(神经网络的参数)\(f\)的权重参数。
伪代码解释
- 初始化参数\(\theta\)
- wheil:
- 抽取task,就是形成可能由不同内别图片组成的数据集,在作者提供的代码中,设定一个抽取4个Task,作为meta-learning的一个batch。在5-way 5-shot的情境下,作者为一个task抽取了100张照片,也就是5x20,5个类别,每个类别20张图片。task之间的5个类别有可能由重复的类别,也有可能不一样,这个是随机的
- for——对于每个task:
- 采样数据,把数据分成两部分,在5-way 5-shot设定中,一个类别只能使用5个样本来学习,那么把这100张照片分成5x5的训练集,以及5x15的验证集
- 计算使用训练集得到的Loss,在图片分类的实验中,使用的是交叉熵函数。
- 通过Loss来计算SGD,即利用梯度更新得到\(\theta '\)
- 使用验证集在经过6,7步调整的权重下计算test error。6,7,8三个步骤在图片分类的实验中循环了5次
- end for
- 使用4个Task中的test error(5次循环中的最后一次)的平均值作为meta-learning的损失函数,来进行SGD过程
- end while
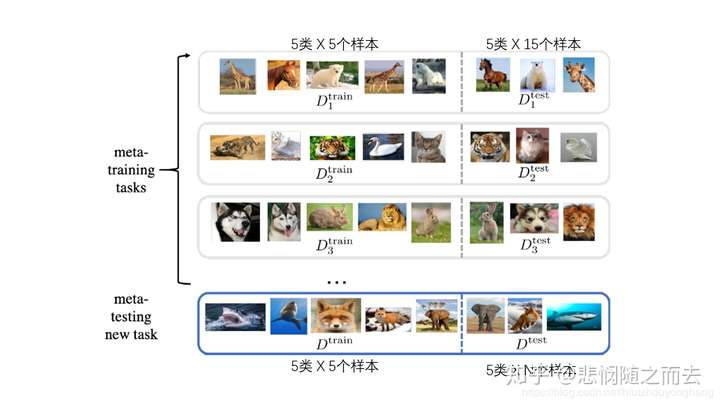
在一个task中,使用左边的训练集做5次SGD的过程,再使用右边的测试集计算test error,在meta-learning过程中,把一个batch的4个task的test error平均一下作为loss再去进行优化。这个过程结束后,神经网络的权重到达了下图中的P点
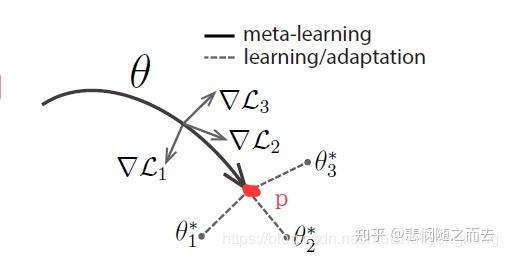
那么,我们再使用这个模型或者测试这个模型的准确度怎么用呢?
例如把100类图片分成了3个子集,train中有64个类,用于上述的meta-learning。
现在要将这个模型用在新的任务集具有16个类的test数据集上。仔细一想,训练好的模型并没有看见过test数据集中任何类。
现在就是要说论文标题中的Fast Adaptation的关键字了,在5-way 5-shot设定中,在测试的时候从test数据集中随机抽取5个类,每个类抽取N(>5)张照片,其中5张照片,用来微调模型中的参数,比如说在一个新任务下,把模型的参数调整至\(\theta^*_3\)的位置,就是task做的事,即在新任务下只用5张照片来学习一下,用剩下的照片来预测并计算精度。
小样本学习要解决什么问题?
举一个例子,假如有如图的两类动物,左边一类是犰狳,右边一类是穿山甲,现在请你仔细区分一下它们。但是我并不告诉你到底什么是犰狳,什么是穿山甲。现在,我新给你一个图像,请你判断是犰狳还是穿山甲。

它显然是穿山甲。这是人的能力,仅仅从一个很小的甚至为1的样本量就可以进行同类或异类的区分。我们希望机器也能够具有这样仅仅根据很小的样本量就可以区分同类和异类的能力。但是这样小的样本不可能用来训练一个深度神经网络,那该怎么办呢?
我们首先回顾一下传统的强监督分类问题。简化来说,我们有一个训练集,训练集中包含很多类别,每个类别下有很多同类样本。现在来了一个测试图片,注意这个测试图片本身是训练集没有见过的,但是!他的类别一定在训练集中有。比如下图所示:测试图片是一个哈士奇,但是在训练集中是有哈士奇这一类,所以网络已经见过很多的哈士奇了。

对于小样本问题,我们还是有训练集,这个训练集和之前传统的强监督的差不多。但是现在这个测试图像(FSL中叫做Query)训练集既没见过,他的类别训练集中也没有!比如下图,训练集中有哈士奇,大象,虎哥,鹦鹉和车五类,测试图片却是一个兔子。但是呢,我们有一些数量很少的卡片,叫做Support Set,它里面包含几个类别(标注),每个类别下有很少量的图片。已知Query一定来自Support Set中的一类。但是Support Set本身又无法支持网络的训练。
现在我们想要让机器和人一样只根据数量很少的样本就能够判断Query是Support Set中的哪一类。这就是小样本学习要解决的问题。

 ‘
‘
小样本学习的几个概念
小样本学习的数据集包含三个,一个是Training Set,一个是Support Set,另一个是Query。我刚学到这里时,对Training Set非常疑惑,既然Query的类别Training Set中都没有,那么为什么我们还需要Training Set?其实我们需要在Training Set上训练网络能够区分同类和异类的能力,这种能力的训练是需要大量样本的。后面就知道啦。
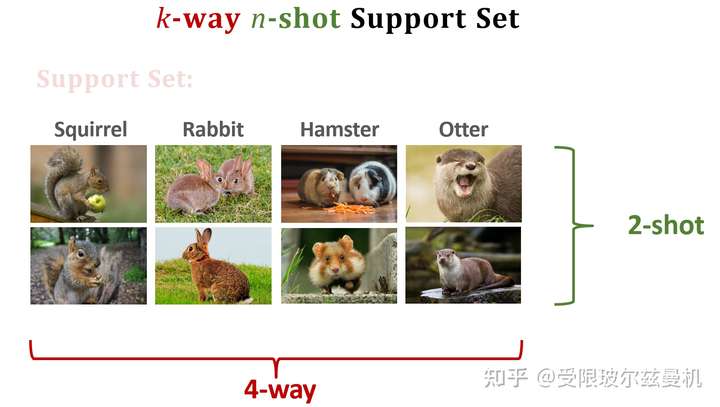
现在我们来看Support Set,Support Set中有k类样本,每类中有n个样本,我们将类别数叫做k-way,将每类中的样本数叫做n-shot。如图中这个就是4-way,2-shot。显然,当way越多n越少的时候,就越困难。注意,当每类下就一个样本时,叫做one-shot,这个是最困难的,也是目前比较火的。

怎么解决?
那我们怎么来解决这个问题呢?最主要的思路也很简单,那就是看Query和Support Set中的哪一类更像呗!用学术语言来说,就是Learn a similarity function。那就得先让网络知道什么是像!但是Support Set中就那么几个,网络学不会啊。这个时候之前说的Training Set就派上用场了。原来我们不是用它来训练一个分类器来分哪一个是虎哥,哪一个是大象,我们是要用它来让网络学习什么是像,什么是不像!
具体来看就是学习下面的这个sim函数,当两张图像是同一类时,sim=1,是不同类的时候sim=0。学会了像以后,就让网络来看Query和Support Set中的哪一个最像,那么Query就属于Support Set中的哪一类。这个问题就解决啦。



让网络学习什么是像,什么是不像
让网络学会什么是像,什么是不像,这是最基本的想法也是最重要的一环。以下简单介绍几种经典的方法。
Learning Pairwise Similarity Scores
这个思想比较简单,既然Training Set中有很多类,每类中也有很多样本,那么就来构造正负样本对来让网络学习哪些是像的,哪些是不像的。
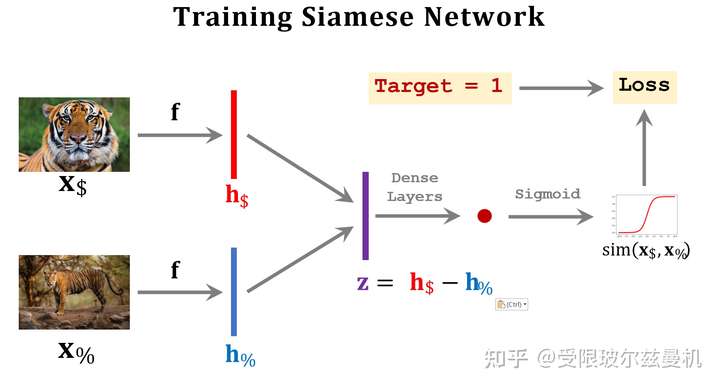
如图所示,训练集中包含五类,我们使用类中的样本构造正样本,即他们是相似的;用类间的样本构造负样本,即他们是不相似的。我们给正样本给予标签1,负样本给予标签0。可以看到,这样构造的话,我们的映射关系,就是输入是一个图像对,标签是0或者1。我们如何设计网络结构呢?


答案是使用孪生网络Siamese Network,它的输入是两个图像,并按照完全相同(共享)的权重将两幅图像映射到embedding中。然后我们将这两个图像在特征空间的embedding求一个距离,或者做差之后通过全连接层进一步映射,最后通过sigmoid函数和我们的标签结合起来。这样网络就可以端到端的来学习什么是像啦。
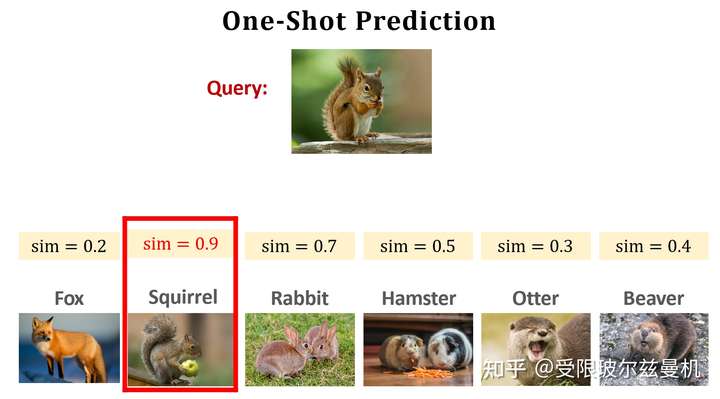
然后呢,我们将Quary与Support Set中的每一个样本均进行以上测试,最后sigmoid输出的sim值越接近1,就说明Quary和这个样本越像,最后找到那个最像的就可以啦!
Triplet Loss
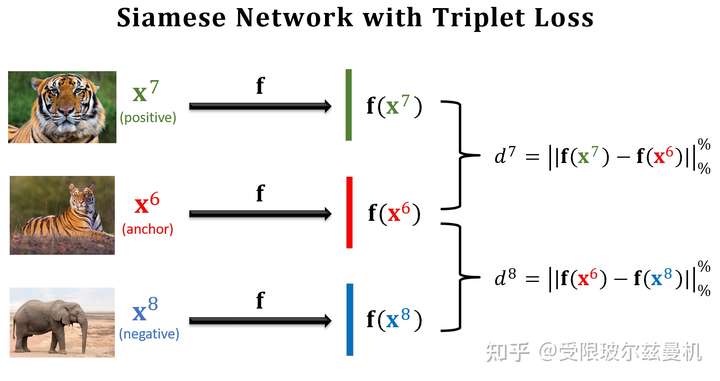
之前我们构造样本对每次都是一个正样本对一个负样本对这样来构造,这样其实并不能很明显的进行对比。于是三个样本的构造方法就出现了。首先我们在测试集中的某一类中选择一个锚点样本,比如那个虎哥。然后我们在虎哥所在的这一类中,再选一个虎弟作为正样本;然后不在虎这一类里面选了,再到其他类里面选一个作为负样本。这样我们就选好了三个样本。



然后我们依然使用孪生网络来进行特征提取,只不过现在在一次训练的过程中,我们计算两个正样本之间的特征距离和两个负样本之间的特征距离,接下来就是定义损失函数了。
对于正样本们,我们当然希望它们在特征空间的距离尽可能地靠近,近成0了那最好;
对于负样本对,我们尽可能地希望它们在特征空间的距离尽可能远离,那么多远就算远了呢,我们需要给定一个条件。因此我们定义一个\(\alpha\),当两个负样本之间的距离比正样本之间的距离远到α的时候,我们就认为足够了,loss=0,这样正样本之间的距离太远了不行,负样本之间的距离太近了也不行。所以这种思想是一种对比的思想,将相似的样本在特征空间拉近,而将不相似的样本在特征空间推远。

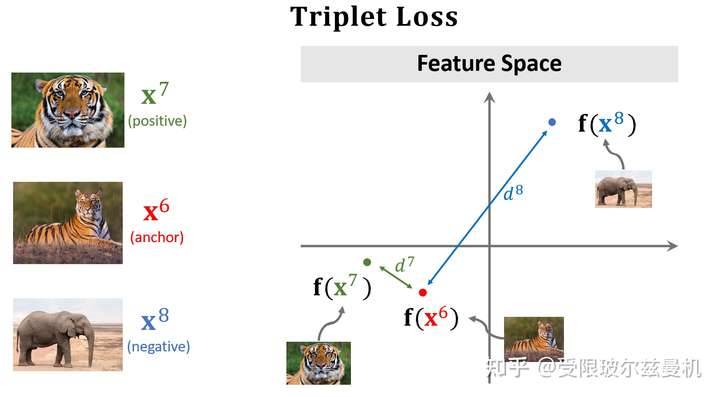
之后我们来进行预测,我们分别计算Quary和每个样本之间的距离,选距离最小的那个作为最终的决策类。

Pretraining and Fine-tuning
我们之前的思路是在训练集上让网络学会什么是像,然后直接测试Quary和Support Set。其实Support Set在训练集中也没有,甚至连类别都没有见过,网络可能会有点害怕。那么能不能让网络也见见Support Set呢,答案是可以的!而且能涨好多点!
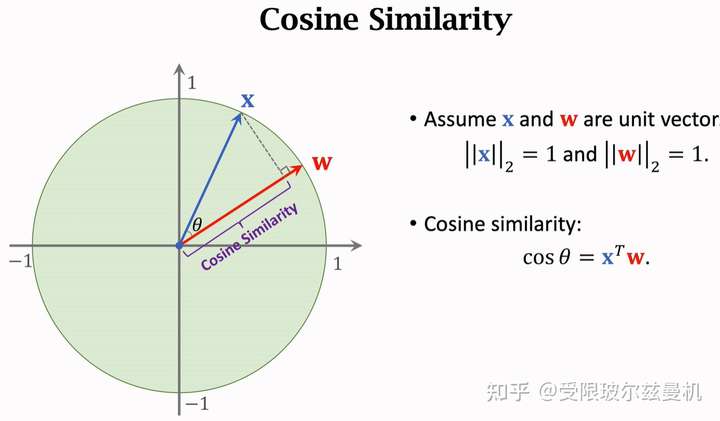
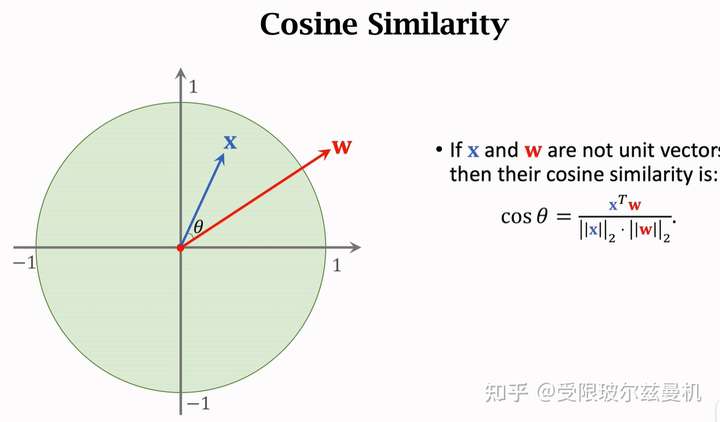
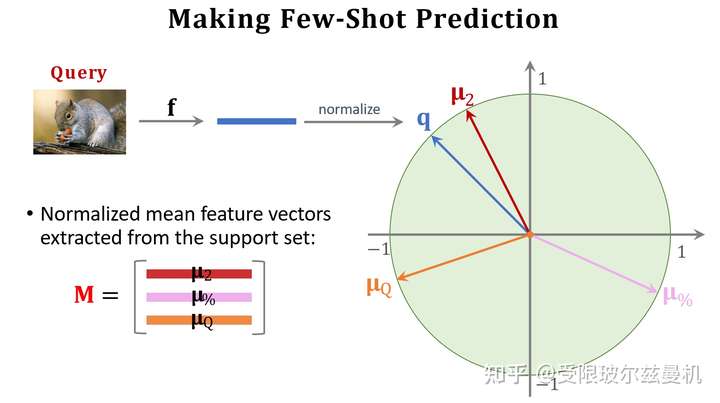
首先我们从余弦相似度说起,已知两个单位向量,它们之间的余弦相似度就是它们的内积,当夹角越小的时候,两个向量更像。因此余弦相似度可以表示两个向量的相似程度,常常用在特征空间。当两个向量不是单位向量时,需要先对其进行归一化,然后再求内积。
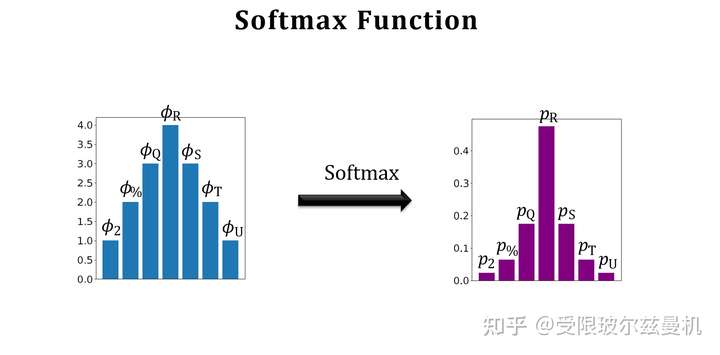
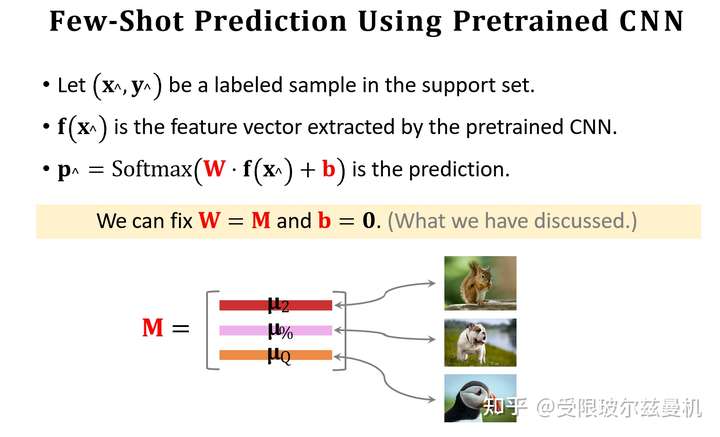
我们再来说Softmax函数。Softmax函数可以将一组数转化为每个数对应的概率值,概率和为1。当然,这样转化会使本来大的数更大,但是却比直接max要温和。那么所谓的softmax分类器,无非就是将一个d1的输入向量左乘一个kd的权重矩阵,再加一个偏置,得到对应k类的概率值。这个权重是根据loss计算的。


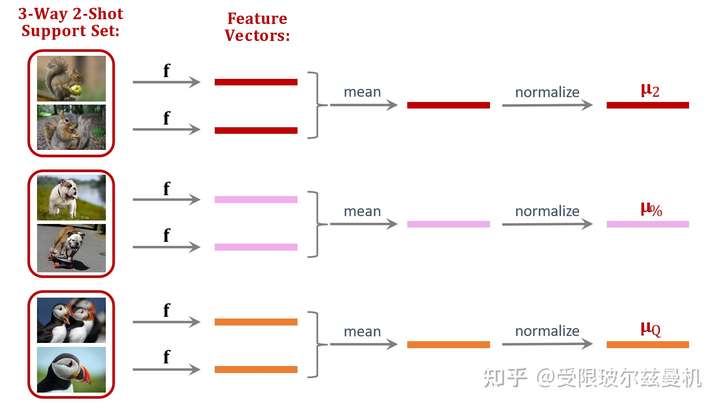
好啦,下面我们开始具体说。我们还是在大型的训练集上训练我们的网络。只不过不直接在Support Set上进行测试。我们将Support Set中的每一类样本使用训练好的网络进行特征提取,如果每一类中有一些样本,那么我们对他们的embedding进行平均。之后我们进行归一化,这是为了后面更好的计算余弦相似度。这样一来我们得到了Support Set中这些类的平均归一化embedding。
接下来我们也对Query提取embedding,并使用之前Support Set提取的embedding初始化权重矩阵M。我们可以看出M中的每一行其实都代表Support Set中每一类的特征。接下来我们使用Support Set中的样本根据softmax分类器进行fintuning。我们使用M来直接初始化softmax的权重矩阵W,这是因为Support Set中的样本数量太少了,如果随机初始化参数,则效果并不好。其实不难发现,我们直接求Q与M的内积再接softmax就可以得到Q属于M中的哪一类的概率,由于没有进行fintuning,它的结果还是差一些。
我们使用M作为初始化权重矩阵,之后使用交叉熵函数对Support Set中的所有样本进行fintuning。

Trick
在fine-tuning的过程中,我们有三个非常好用的Trick。
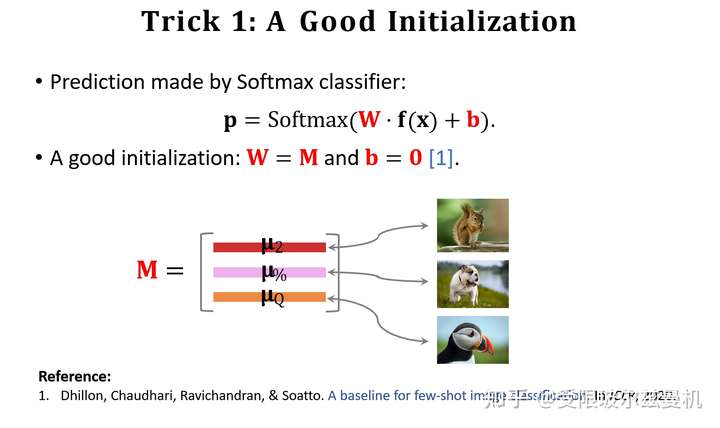
第一个是我们刚才说过的,在fine-tuning的时候使用Support Set中每类样本的特征组成的矩阵M进行初始化待训练权重W,这是因为Support Set中的样本数量太少了,如果随机初始化参数,则效果可能不佳。
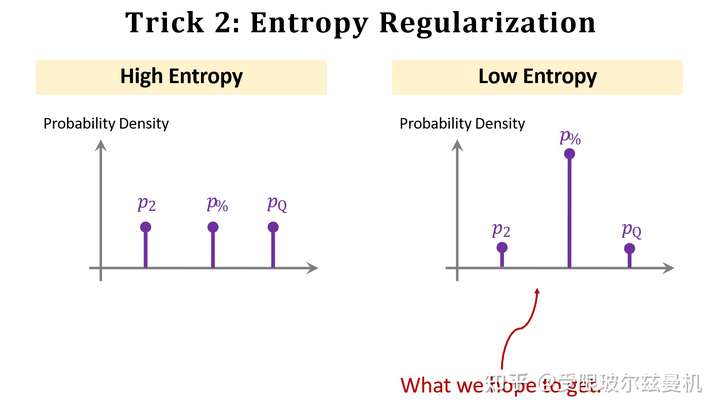
第二个是使用熵进行正则化。我们知道对于softmax,如果他输出每一类的概率都差不多,那么说明分类器没有学好,基本是在瞎猜的状态,此时它的熵就会很大;但是如果有一类输出的概率特别大,其他预测概率都很小,那么说明神经网络此时很有把握,这时它的熵就会很小。我们希望fintuning中神经网络能给出更有把握的结果,因此加入熵正则化,可以明显提高性能。

第三个是使用余弦相似度与softmax分类器的组合。我们知道softmax分类器中是权重W与Q相乘来运算的,而我们这里将这个W替换为余弦相似度的计算,也可以提高性能。

本文来自博客园,作者:甫生,转载请注明原文链接:https://www.cnblogs.com/fusheng-rextimmy/p/15450827.html

