YOLO V1

YOLOV1

paper link

You Only Look Once: Unified, Real-Time Object Detection

物体检测算法概述

物体检测（object detection）是计算机视觉中一个重要的分支，其大致功能是在一张图片中，用最小矩形框框出目标物体位置，并进行分类。先上图，Yolo v1可以识别20个类别：

物体检测的两个步骤可以概括为：

步骤一：检测目标位置（生成矩形框）

步骤二：对目标物体进行分类

物体检测主流的算法框架大致分为one-stage与two-stage。two-stage算法代表有R-CNN系列，one-stage算法代表有Yolo系列。按笔者理解，two-stage算法将步骤一与步骤二分开执行，输入图像先经过候选框生成网络（例如faster rcnn中的RPN网络），再经过分类网络；one-stage算法将步骤一与步骤二同时执行，输入图像只经过一个网络，生成的结果中同时包含位置与类别信息。two-stage与one-stage相比，精度高，但是计算量更大，所以运算较慢。

就R-CNN系列算法与Yolo系列算法简单列出发表时间线：

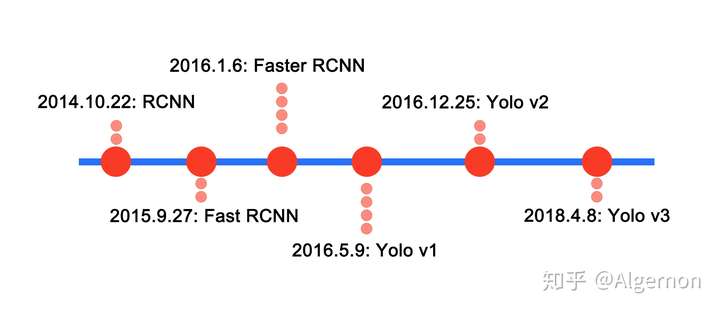
可见，Yolo系列发表日期全部在Faster RCNN之后，Faster RCNN算法的精度是state-of-the-art级别的，Yolo算法的精度没有超越Faster RCNN，而是在速度与精度之间进行权衡。

Yolov3在改进多次之后，既有一定的精度，也保持了较高的运行速度。在很多边缘计算、实时性要求较高的任务中，Yolov3备受青睐。在RCNN算法日益成熟之后，Yolo算法却能横空出世，离不开其高性能和使用回归思想做物体检测的两个特点。

First, YOLO is extremely fast. Since we frame detection as a regression problem we don’t need a complex pipeline.
Second, YOLO reasons globally about the image when making predictions. Unlike sliding window and region proposal-based techniques, YOLO sees the entire image.
Third, YOLO learns generalizable representations of objects. When trained on natural images and tested on art- work, YOLO outperforms top detection methods like DPM and R-CNN by a wide margin.

1. Yolo很快，因为用回归的方法，并且不用复杂的框架。
2. Yolo会基于整张图片信息进行预测，而其他滑窗式的检测框架，只能基于局部图片信息进行推理。
3. Yolo学到的图片特征更为通用。作者尝试了用自然图片数据集进行训练，用艺术画作品进行预测，Yolo的检测效果更佳。

算法工作流程

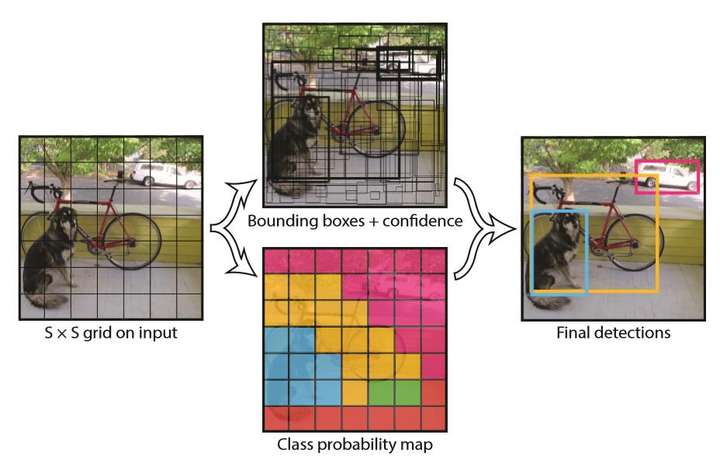
(1) 将原图划分为SxS的网格。如果一个目标的中心落入某个格子，这个格子就负责检测该目标。

(2) 每个网格要预测B个bounding boxes，以及C个类别概率Pr(classi|object)。这里解释一下，C是网络分类总数，由训练时决定。在作者给出的demo中C=20，包含以下类别：

人person、鸟bird、猫cat、牛cow、狗dog
马horse、羊sheep、飞机aeroplane、自行车bicycle
船boat、巴士bus、汽车car、摩托车motorbike
火车train、瓶子bottle、椅子chair、餐桌dining table
盆景potted plant、沙发sofa、显示器tv/monitor

在YOLO中，每个格子只有一个C类别，即相当于忽略了B个bounding boxes，每个格子只判断一次类别，这样做非常简单粗暴。

(3) 每个bounding box除了要回归自身的位置之外，还要附带预测一个confidence值。这个confidence代表了所预测的box中含有目标的置信度和这个bounding box预测的有多准两重信息：

\[confidence=Pr(object)\cdot IoI^{truth}_{pred} \]

如果有目标落中心在格子里Pr(Object)=1；否则Pr(Object)=0。 第二项是预测的bounding box和实际的ground truth之间的IOU。

所以，每个bounding box都包含了5个预测量：\((x, y, w, h, confidence)\)，其中\((x, y)\)代表预测box相对于格子的中心，\((w, h)\)为预测box相对于图片的width和height比例，\(confidence\)就是上述置信度。需要说明，这里的\(x,y,w,h\)都是经过归一化的，之后有解释。

(4) 由于输入图像被分为SxS网格，每个网格包括5个预测量：(x, y, w, h, confidence)和一个C类，所以网络输出是SxSx(5xB+C)大小

(5) 在检测目标的时候，每个网格预测的类别条件概率和bounding box预测的confidence信息相乘，就得到每个bounding box的class-specific confidence score:

\[Pr(Class_i|Object)*Pr(object)*IoU^{truth}_{pred}=Pr(Class_i)*IoU^{truth}_{pred} \]

显然这个class-specific confidence score既包含了bounding box最终属于哪个类别的概率，又包含了bounding box位置的准确度。最后设置一个阈值与class-specific confidence score对比，过滤掉score低于阈值的boxes，然后对score高于阈值的boxes进行非极大值抑制(NMS, non-maximum suppression)后得到最终的检测框体。

Yolo v1算法原理

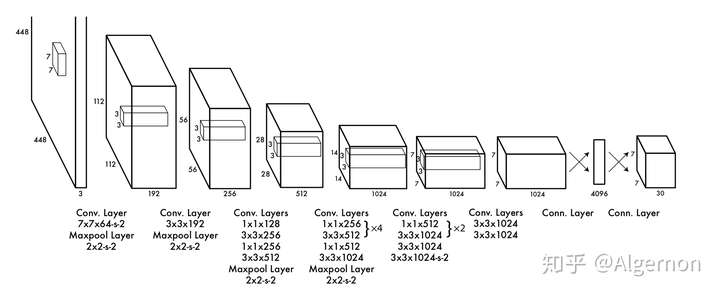
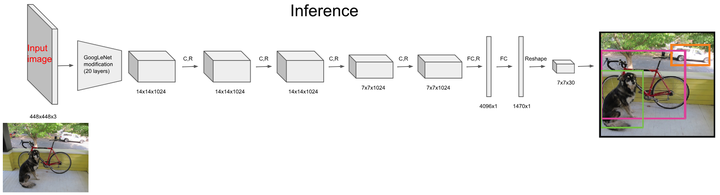
直接上结构图，输入图像大小为\(448*448\)，经过若干个卷积层与池化层，变为\(7*7*1024\)张量（图一中倒数第三个立方体），最后经过两层全连接层，输出张量维度为\(7*7*30\)，这就是Yolo v1的整个神经网络结构，和一般的卷积物体分类网络没有太多区别，最大的不同就是：分类网络最后的全连接层，一般连接于一个一维向量，向量的不同位代表不同类别，而这里的输出向量是一个三维的张量（\(7*7*30\)）。

\(conv\ layer \ 7*7*64-s-2\)中\(7*7*64\)是是卷积核尺寸，\(s-2\)就是滑动步长为2

上图中Yolo的backbone网络结构，受启发于GoogLeNet，也是v2、v3中Darknet的先锋。本质上来说没有什么特别，没有使用BN层，用了一层Dropout。除了最后一层的输出使用了线性激活函数，其他层全部使用Leaky Relu激活函数。网络结构没有特别的东西，不再赘述。

注：Yolo的backbone指的就是和传统分类网络交叉的用于特征提取的部分，上图中除了最后两层FC都算是backbone，对应yolov3的darknet-53

网络输出张量纬度

\(7*7\)的含义

\(7*7\)指的是图片被分割成了\(7*7\)个格子

在Yolo中，如果一个物体的中心点，落在了某个格子中，那么这个格子将负责预测这个物体。这句话怎么理解，用上图举例，设左下角格子假设坐标为\((1,1)\)，小狗所在的最小包围矩形框的中心，落在了\((2,3)\)这个格子中。那么\(7*7\)个格子中，\((2,3)\)这个格子负责预测小狗，而那些没有物体中心点落进来的格子，则不负责预测任何物体。这个设定就好比该网络在一开始，就将整个图片上的预测任务进行了分工，一共设定\(7*7\)个按照方阵列队的检测人员，每个人员负责检测一个物体，大家的分工界线，就是看被检测物体的中心点落在谁的格子里。当然，是\(7*7\)还是\(9*9\)，是上图中的参数\(S\)，可以自己修改，精度和性能会随之有些变化。

30的含义

刚才设定了49个检测人员，那么每个人员负责检测的内容，就是这里的30（注意，30是张量最后一维的长度）。在Yolo v1论文中，30是由\((4+1)*2+20\)得到的。其中4+1是矩形框的中心点坐标\(x,y\)，长宽\(w,h\)以及是否属于被检测物体的置信度\(c\)；2是一个格子共回归两个矩形框，每个矩形框分别产生5个预测值\((x,y,w,h,c)\)；20代表预测20个类别。

这里有几点需要注意：

1. 每个方格（grid） 产生2个预测框，2也是参数，可以调，但是一旦设定为2以后，那么每个方格只产生两个矩形框，最后选定置信度更大的矩形框作为输出，也就是最终每个方格只输出一个预测矩形框。

   （anchor锚框的定义）每个格子预测矩形框个数，是可调超参数；论文中选择了2个框，当然也可以只预测1个框，具体预测几个矩形框，无非是在计算量和精度之间取一个权衡。如果只预测一个矩形框，计算量会小很多，但是如果训练数据都是小物体，那么网络学习到的框，也会普遍比较小，测试时如果物体较大，那么预测效果就会不理想；如果每个格子多预测几个矩形框，如上文中讲到的，每个矩形框的学习目标会有所分工，有些学习小物体特征，有些学习大物体特征等；在Yolov2、v3中，这个数目都有一定的调整。至于v1为什么选择了2，估计也是作者多次实验后，在速度和精度综合考虑后得到的吧。

2. 每个方格只能预测一个物体。虽然可以通过调整参数，产生不同的矩形框，但这只能提高矩形框的精度。所以当有很多个物体的中心点落在了同一个格子里，该格子只能预测一个物体。也就是格子数为7*7时，该网络最多预测49个物体。

YOLO imposes strong spatial constraints on bounding box predictions since each grid cell only predicts two boxes and can only have one class. This spatial constraint limits the number of nearby objects that our model can predict. Our model struggles with small objects that appear in groups, such as flocks of birds.

因为在强行施加了格点限制以后，每个格点只能输出一个预测结果，所以该算法最大的不足，就是对一些邻近小物体的识别效果不是太好，例如成群结队的小鸟。

Loss function

看到这里读者或许会有疑问，Yolo里的每个格点，是怎么知道该预测哪个物体的？这就是神经网络算法的能力。首先拿到一批标注好的图片数据集，按照规则打好标签，之后让神经网络去拟合训练数据集。训练数据集中的标签是通过人工标注获得，当神经网络对数据集拟合的足够好时，那么就相当于神经网络具备了一定的和人一样的识别能力。

神经网络结构确定之后，训练效果好坏，由Loss函数和优化器决定。Yolo v1使用普通的梯度下降法作为优化器。这里重点解读一下Yolo v1使用的Loss函数：

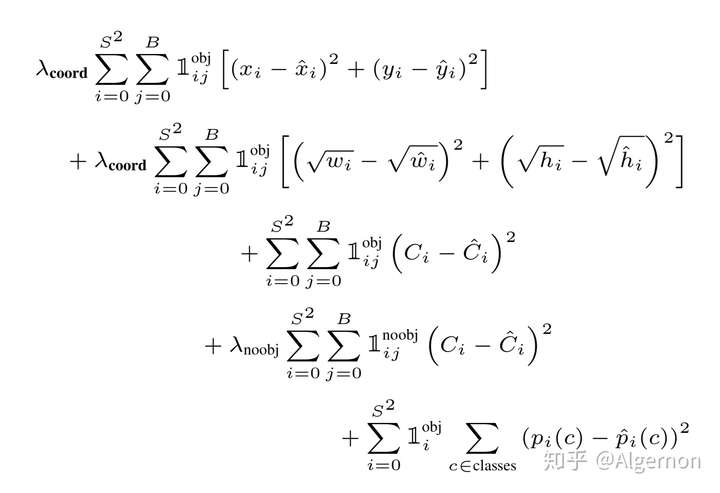
论文中Loss函数，密密麻麻的公式初看可能比较难懂。其实论文中给出了比较详细的解释。所有的损失都是使用平方和误差公式，暂时先不看公式中的\(\lambda_{coord},\lambda_{noobj}\) ，输出的预测数值以及所造成的损失有:

1. 预测框的中心点\((x,y)\)

   造成的损失对应公式中的第一行，其中\(1^{obj}_{ij}\)为控制函数，在标签中包含物体的那些格点处，该值为 1 ；若格点不含有物体，该值为 0。也就是只对那些有真实物体所属的格点进行损失计算，若该格点不包含物体，那么预测数值不对损失函数造成影响。\((x,y)\)数值与标签用简单的平方和误差。

2. 预测框的宽高\((w,h)\)

   造成的损失对应公式中的第二行，其中\(1^{obj}_{ij}\)的含义一样，也是使得只有真实物体所属的格点才会造成损失。这里对\((w,h)\)在损失函数中的处理分别取了根号，原因在于，如果不取根号，损失函数往往更倾向于调整尺寸比较大的预测框。例如，20个像素点的偏差，对于\(800*600\)的预测框几乎没有影响，此时的IOU数值还是很大，但是对于\(30*40\)的预测框影响就很大。取根号是为了尽可能的消除大尺寸框与小尺寸框之间的差异。

3. 第三行与第四行，都是预测框的置信度C。

   当该格点不含有物体时，该置信度的标签为0，即Pr(object)=0。

   若含有物体时，该置信度的标签为预测框与真实物体框的IoU数值。（IoU计算公式为：两个框交集的面积除以并集的面积）v1作者用的IoU，v3就变成1了。1确实收敛更稳定

   即不包含obj的置信度损失包含两部分，一部分是包含obj的grid cell中的两个BBox中不负责预测的那个BBox，另外一部分是不包含obj的grid cell的bbox。损失计算时，负责预测物体的bbox的标签值就是IoU的值，不负责预测物体的bbox的标签值就是0（包含上述所描述的两部分），预测值就是网络直接输出出来的，计算时就是两者相减后取平方。

   置信度的意义在于表征该预测框预测的准确程度,即预测框位置与目标框位置接近程度,该程度用IoU表示

   IoU是置信度的标签，因为包含物体的格点与不包含物体的格点，都会输出预测框坐标，至于谁是真正的包含物体的格点，由置信度来控制。

4. 第五行为物体类别概率P，对应的类别位置，该标签数值为1，其余位置为0，与分类网络相同。

   此处注释一下，类别编号采用的one-hot编码，1对应的index就是类别。最后预测的时候是用每个类别单独预测的概率，乘以IoU，每个类别单独预测的概率在0、1之间的

it also only penalties bounding box coordinate error if that predictor is responsible for the ground truth box (i.e. has the highest IOU of any predictor in that grid cell.

由原文可知，损失函数仅对某格点产生的IOU最大的框框计算坐标轴相关的损失。

此时再来看\(\lambda_{coord},\lambda_{noobj}\)，Yolo面临的物体检测问题，是一个典型的类别数目不均衡的问题。其中49个格点，含有物体的格点往往只有3、4个，其余全是不含有物体的格点。此时如果不采取点措施，那么物体检测的mAP不会太高，因为模型更倾向于不含有物体的格点。\(\lambda_{coord},\lambda_{noobj}\)的作用，就是让含有物体的格点，在损失函数中的权重更大，让模型更加“重视”含有物体的格点所造成的损失。在论文中，\(\lambda_{coord},\lambda_{noobj}\)的取值分别为5与0.5。

some tricks

1. 回归offset代替直接回归坐标

   We parametrize the bounding box x and y coordinates to be offsets of a particular grid cell location so they are also bounded between 0 and 1

   \((x,y)\)不直接回归中心点坐标数值，而是回归相对于格点左上角坐标的位移值。例如，第一个格点中物体坐标为\((2.3,3.6)\)，另一个格点中的物体坐标为\((5.4,6.3)\)这四个数值让神经网络暴力回归，有一定难度。所以这里的offset是指，既然格点已知，那么物体中心点的坐标一定在格点正方形里，相对于格点左上角的位移值一定在区间\([0, 1)\)中。让神经网络去预测\((0.3,0.6)\)与\((0.4,0.3)\) 会更加容易，在使用时，加上格点左上角坐标\((2,3)、(5,6)\)即可

2. 同一格点的不同预测框有不同作用

   At training time we only want one bounding box predictor to be responsible for each object. We assign one predictor to be “responsible” for predicting an object based on which prediction has the highest current IOU with the ground truth. This leads to specialization between the bounding box predictors. Each predictor gets better at predicting certain sizes, aspect ratios, or classes of object, improving overall recall.

   前文中提到，每个格点预测两个或多个矩形框。此时假设每个格点预测两个矩形框。那么在训练时，见到一个真实物体，我们是希望两个框都去逼近这个物体的真实矩形框，还是只用一个去逼近？或许通常来想，让两个人一起去做同一件事，比一个人做一件事成功率要高，所以可能会让两个框都去逼近这个真实物体。但是作者没有这样做，在损失函数计算中，只对和真实物体最接近的框计算损失，其余框不进行修正。这样操作之后作者发现，一个格点的两个框在尺寸、长宽比、或者某些类别上逐渐有所分工，总体的召回率有所提升。

3. 使用非极大抑制(NMS)生成预测框

   However, some large objects or objects near the border of multiple cells can be well localized by multiple cells. Non-maximal suppression can be used to fix these multiple detections. While not critical to performance as it is for R-CNN or DPM, non-maximal suppression adds 2 - 3% in mAP.

   通常来说，在预测的时候，格点与格点并不会冲突，但是在预测一些大物体或者邻近物体时，会有多个格点预测了同一个物体。此时采用非极大抑制技巧，过滤掉一些重叠的矩形框。但是mAP提升并没有显著提升。（非极大抑制，物体检测的老套路，这里不再赘述）

4. 推理时将\(p*c\)作为输出置信度

   条件概率定义为\(Pr(Class_i|Object)\)，表示该单元格存在物体且属于第i类的概率

   \[Pr(Class_i|Object)*Pr(object)*IOU^{truth}_{pred}=Pr(Class_i)*IOU^{truth}_{pred} \]

   在测试的时候每个单元格预测最终输出的概率定义为，如下两图所示（两幅图不一样，代表一个框会输出B列概率值）

   

   

   在推理时，使用物体的类别预测最大值\(p\)乘以 预测框的最大值\(c\)，作为输出预测物体的置信度。这样也可以过滤掉一些大部分重叠的矩形框。输出检测物体的置信度，同时考虑了矩形框与类别，满足阈值的输出更加可信。

YOLO中的Bounding Box Normalization

YOLO在实现中有一个重要细节，即对bounding box的坐标(x, y, w, h)进行了normalization，以便进行回归。作者认为这是一个非常重要的细节。在原文2.2 Traing节中有如下一段：

Our final layer predicts both class probabilities and bounding box coordinates.
We normalize the bounding box width and height by the image width and height so that they fall between 0 and 1.
We parametrize the bounding box x and y coordinates to be offsets of a particular grid cell location so they are also bounded between 0 and 1.

接下来分析一下到底如何实现。

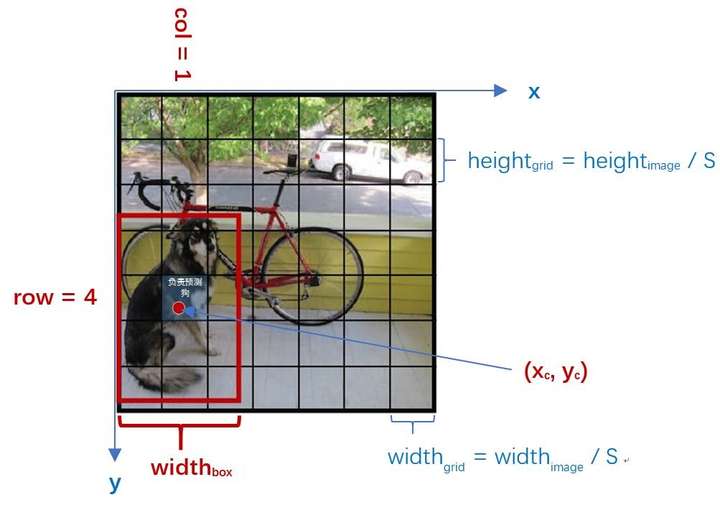
如上图，在YOLO中输入图像被分为SxS网格。假设有一个bounding box，其中心刚好落在了(row,col)网格中，则这个网格需要负责预测整个红框中的dog目标。假设图像的宽为widthimage，高为heightimage；红框中心在(xc，yc)，宽为widthbox，高为heightbox那么：

(1) 对于bounding box的宽和高做如下normalization，使得输出宽高介于0~1：

\[\begin{matrix}w=\frac{width_{box}}{width_{image}}\\h=\frac{height_{box}}{height_{image}}\end{matrix} \]

(2) 使用(row, col)网格的offset归一化bounding box的中心坐标：

\[\begin{matrix}x=x_c\cdot \frac{S}{width_{image}}-col=\frac{x_c}{width_{grid}}-col\\y=y_c\cdot \frac{S}{height_{image}}-row=\frac{y_c}{height_{grid}}-row\end{matrix} \]

经过上述公式得到的normalization的(x, y, w, h)，再加之前提到的confidence，共同组成了一个真正在网络中用于回归的bounding box；

而当网络在Test阶段(x,y,w,h)经过反向解码又可得到目标在图像坐标系的框，相关解码代码在darknet框架detection_layer.c中的get_detection_boxes()函数，关键部分如下：

boxes[index].x = (predictions[box_index + 0] + col) / l.side * w;
boxes[index].y = (predictions[box_index + 1] + row) / l.side * h;
boxes[index].w = pow(predictions[box_index + 2], (l.sqrt?2:1)) * w;
boxes[index].h = pow(predictions[box_index + 3], (l.sqrt?2:1)) * h;

而w和h就是图像宽高，l.side是上文中提到的S。

Yolo训练过程

对于任何一种网络，loss都是非常重要的，直接决定网络效果的好坏。YOLO的Loss函数设计时主要考虑了以下3个方面

(1) bounding box的(x, y, w, h)的坐标预测误差。在检测算法的实际使用中，一般都有这种经验：对不同大小的bounding box预测中，相比于大box大小预测偏一点，小box大小测偏一点肯定更不能被忍受。所以在Loss中同等对待大小不同的box是不合理的。为了解决这个问题，作者用了一个比较取巧的办法，即先对w和h求平方根压缩数值范围，再进行回归。

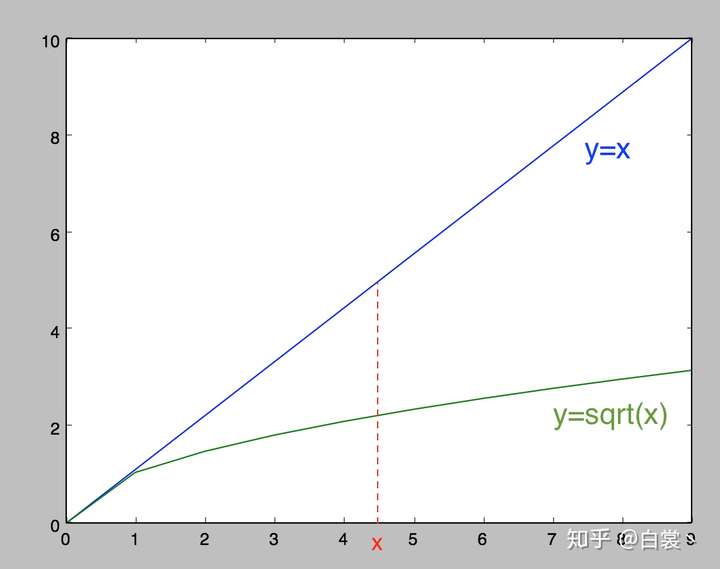
从后续效果来看，这样做有效，但是没有完全解决问题。

(2) bounding box的confidence预测误差。由于绝大部分网格中不包含目标，导致绝大部分box的confidence=0，所以在设计confidence误差时同等对待包含目标和不包含目标的box也是不合理的，否则会导致模型不稳定。作者在不含object的box的confidence预测误差中乘以惩罚权重\(\lambda_{noonj}=0.5\)

除此之外，同等对待4个值(x, y, w, h)的坐标预测误差与1个值的conference预测误差也不合理，所以作者在坐标预测误差误差之前乘以权重\(\lambda_{coord}=5\)

(3) 分类预测误差。即每个box属于什么类别，需要注意一个网格只预测一次类别，即默认每个网格中的所有B个bounding box都是同一类。所以，YOLO的最终误差为下：

Loss = λcoord *** 坐标预测误差 + （含object的box confidence预测误差 + λnoobj** *** 不含object的box confidence预测误差） + 类别预测误差**

1.每个图片的每个单元格不一定都包含object，如果没有object，那么confidence就会变成0，这样在优化模型的时候可能会让梯度跨越太大，模型不稳定跑飞了。为了平衡这一点，在损失函数中，设置两个参数\(\lambda_{coord}\)和\(\lambda_{noobj}\)，其中\(\lambda_{coord}\)控制bbox预测位置的损失，控制单\(\lambda_{noobj}\)个格内没有目标的损失。
2.对于大的物体，小的偏差对于小的物体影响较大，为了减少这个影响，所以对bbox的宽高都开根号。

在各种常用框架中实现网络中一般需要完成forward与backward过程，forward函数只需依照Loss编码即可，而backward函数简需要计算残差delta。这里单解释一下YOLO的负反馈，即backward的实现方法。在UFLDL教程中网络正向传播方式定义为：

\[\begin{matrix}z^{(l+1)}=W^{(l)}a^{(l)}+b^{(l)}\\a^{(l+1)}=f(z^{(l+1)})\end{matrix} \]

而最后一层反向传播残差定义为：

\[\delta_i^{(n_i)}=\frac{\delta}{\delta z_i^{(n_i)}}\frac{1}{2}\left \| y-h_{W,b}(x)\right \|^2=-(y_i-a_i^{(n_i)})\cdot f'(z_i^{(n_i)}) \]

对于YOLO来说，最后一层是detection_layer，而倒数第二层是connected_layer（全连接层），之间没有ReLU层，即相当于最后一层的激活函数为：

\[f(x)=x \]

那么，对于detection_layer的残差就变为：

\[\delta_i^{(n_l)}=-(y_i-a_i^{(n_l)})\cdot 1=a_i^{(n_l)}-y_i \]

只需计算每一项的参数训练目标值与网络输出值之差，反向回传即可，与代码对应。其他细节读者请自行分析代码，不再介绍。

进一步理解Yolo

1. 在YOLO网络中，首先通过一组CNN提取feature maps
2. 然后通过最后一个全连接FC层生成SxSx(5*B+C)=7x7x(5*2+20)=1470长的向量
3. 再把1470向量reshape成SxSx(5*B+C)=7x7x30形状的多维矩阵
4. 通过解析多维矩阵获得Detection bounding box + Confidence
5. 最后对Detection bounding box + Confidence进行Non maximum suppression获得输出

在设置好网络，并进行初始化后，通过forward就可以获得我们需要的SxSx(5B+C)矩阵，只不过其中数值并不是我们想要的。当经过上述YOLO Loss下的负反馈训练后，显然就可以获得我们SxSx(5B+C)矩阵，再经过解析+NMS就可以获得输出框了。

从本质上说，Faster RCNN通过对Anchors的判别和修正获得检测框；而YOLO通过强行回归获得检测框。

Yolo v1与其他算法比较

与其他算法比较的结论照搬论文，如下性能的硬件环境都是GPU Titan X。

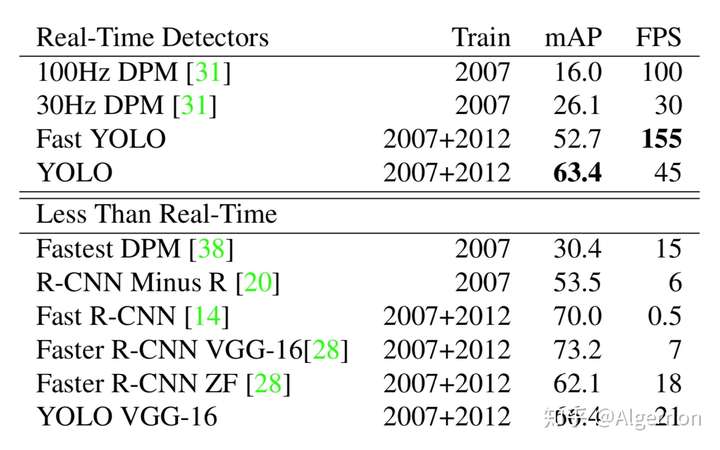
backbone同为VGG-16，Yolo比Faster R-CNN少了将近7点mAP，但是速度变为三倍，Fast Yolo和Yolo相比，少11点mAP，但是速度可以达到155张图片每秒。后续的Yolo v3中，准确率和速度综合再一次提升，所以v1的性能不再过多分析。

下面重点看论文中的错误分析：

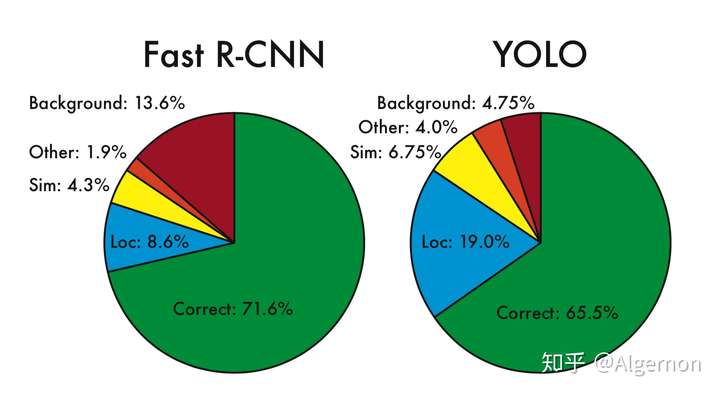
首先给出图中各个单词的含义：

• Correct: correct class and IOU > .5
• Localization: correct class, .1 < IOU < .5
• Similar: class is similar, IOU > .1
• Other: class is wrong, IOU > .1
• Background: IOU < .1 for any object

其中，Yolo的Localization错误率更高，直接对位置进行回归，确实不如滑窗式的检测方式准确率高。但是Yolo对于背景的误检率更低，由于Yolo在推理时，可以“看到”整张图片，所以能够更好的区分背景与待测物体。作者提到Yolo对于小物体检测效果欠佳，不过在v2与v3中都做了不少改进。

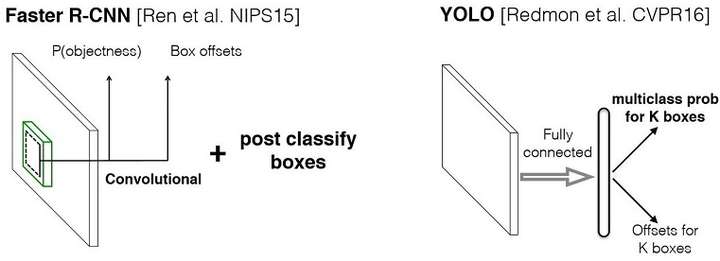
YOLO与Faster RCNN的区别

1. Faster RCNN将目标检测分解为分类为题和回归问题分别求解：首先采用独立的RPN网络专门求取region proposal，即计算下图中的P(objetness)；然后对利用bounding box regression对提取的region proposal进行位置修正，即计算下图中的Box offsets（回归问题）；最后采用softmax进行分类（分类问题）。
2. YOLO将物体检测作为一个回归问题进行求解：输入图像经过一次网络，便能得到图像中所有物体的位置和其所属类别及相应的置信概率。

概念解释

backbone

backbone这个单词原意指的是人的脊梁骨，后来引申为支柱，核心的意思。

主干网络，用来做特征提取的网络，代表网络的一部分，一般是用于前端提取图片信息，生成特征图feature map,供后面的网络使用。通常用VGGNet还有Resnet，因为这些backbone特征提取能力是很强，并且可以加载官方在大型数据集(Pascal 、Imagenet)上训练好的模型参数，然后接自己的网络，进行微调finetune即可。

在神经网络中，尤其是CV领域，一般先对图像进行特征提取（常见的有vggnet，resnet，谷歌的inception），这一部分是整个CV任务的根基，因为后续的下游任务都是基于提取出来的图像特征去做文章（比如分类，生成等等）。

非极大抑制(NMS)

Non-Maximum Suppression的翻译是非“极大值”抑制，而不是非“最大值”抑制。这就说明了这个算法的用处：找到局部极大值，并筛除（抑制）邻域内其余的值。

这是一个很基础的，简单高效且适用于一维到多维的常见算法。因为特别适合目标检测问题，所以一直沿用至今，随着目标检测研究的深入和要求的提高（eg：原来只想框方框，现在想框多边形框），NMS也延伸出了不少变体。

Why&When&How NMS？

非极大值抑制（Non-Maximum Suppression，NMS），顾名思义就是抑制不是极大值的元素，可以理解为局部最大搜索。

这个局部代表的是一个邻域，邻域的“维度”和“大小”都是可变的参数。

NMS在计算机视觉领域有着非常重要的应用，如视频目标跟踪、3D重建、目标识别以及纹理分析等。

Why NMS?

首先，目标检测与图像分类不同，图像分类往往只有一个输出，但目标检测的输出个数却是未知的。除了Ground-Truth（标注数据）训练，模型永远无法百分百确信自己要在一张图上预测多少物体。

所以目标检测问题的老大难问题之一就是如何提高召回率。召回率（Recall）是模型找到所有某类目标的能力（所有标注的真实边界框有多少被预测出来了）。检测时按照是否检出边界框与边界框是否存在，可以分为下表四种情况：

	检测出边界框	未检出边界框
边界框存在	真阳性（TP）	假阴性（FN）
边界框不存在	误报（FP）	真阴性（TN）

召回率Recall公式如下：

\[Recall=\frac{TP}{TP+FN} \]

为了提高这个值，很直观的想法是“宁肯错杀一千，绝不放过一个”。因此在目标检测中，模型往往会提出远高于实际数量的区域提议（Region Proposal，SSD等one-stage的Anchor也可以看作一种区域提议）。

这就导致最后输出的边界框数量往往远大于实际数量，而这些模型的输出边界框往往是堆叠在一起的。因此，我们需要NMS从堆叠的边框中挑出最好的那个。

When NMS?

我们来回顾一下R-CNN的流程：

1. 提议区域
2. 提取特征
3. 目标分类
4. 回归边框

NMS使用在4. 回归边框之后，即所有的框已经被分类且精修了位置。且所有区域提议的预测结果已经由置信度与阈值初步筛选之后。

How NMS?

一维简单例子

由于重点是二维（目标检测）的实现，因此一维只放出伪代码便于理解。

判断一维数组\(I[W]\)的元素\(I[i](2<=i<=W-1)\)是否为局部极大值，即大于其左邻元素\(I[i-1]\)和右邻元素\(I[i+1]\)

算法流程如下图所示：

算法流程3-5行判断当前元素是否大于其左邻与右邻元素，如符合条件，该元素即为极大值点。对于极大值点\(I[i]\)，已知\(I[i]>I[i+1]\)，故无需对\(i+1\)位置元素做进一步处理，直接跳至\(i+2\)位置，对应算法流程第12行。

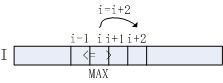
若元素\(I[i]\)不满足算法流程第3行判断条件，将其右邻\(I[i+1]\)作为极大值候选，对应算法流程第7行。采用单调递增的方式向右查找，直至找到满足\(I[i]>I[i+1]\)的元素，若\(i<=W-1\)，该点即为极大值点，对应算法流程第10-11行。

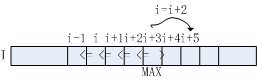
推广到目标检测

首先，根据之前分析确认NMS的前提，输入与输出。

• 使用前提

  • 目标检测模型已经完成了整个前向计算，并给出所有可能的边界框（位置已精修）。

• 算法输入

  • 算法对一幅图产生的所有的候选框，每个框有坐标与对应的打分（置信度）。

    如一组5维数组：

    • 每个组表明一个边框，组数是待处理边框数
    • 4个数表示框的坐标：X_max，X_min，Y_max，Y_min
    • 1个数表示对应分类下的置信度

    注意：每次输入的不是一张图所有的边框，而是一张图中属于某个类的所有边框（因此极端情况下，若所有框的都被判断为背景类，则NMS不执行；反之若存在物体类边框，那么有多少类物体则分别执行多少次NMS）。

    除此之外还有一个自行设置的参数：阈值 TH。

• 算法输出

  • 输入的一个子集，同样是一组5维数组，表示筛选后的边界框。

• 算法流程

  1. 将所有的框按类别划分，并剔除背景类，因为无需NMS。
  2. 对每个物体类中的边界框(B_BOX)，按照分类置信度降序排列。
  3. 在某一类中，选择置信度最高的边界框B_BOX1，将B_BOX1从输入列表中去除，并加入输出列表。
  4. 逐个计算B_BOX1与其余B_BOX2的交并比IoU，若IoU(B_BOX1,B_BOX2) > 阈值TH，则在输入去除B_BOX2。
  5. 重复步骤3~4，直到输入列表为空，完成一个物体类的遍历。
  6. 重复2~5，直到所有物体类的NMS处理完成。
  7. 输出列表，算法结束

算法实现

交并比IoU

交并比（Intersection over Union）是目标检测NMS的依据，因此首先要搞懂交并比及其实现。

衡量边界框位置，常用交并比指标，交并比（Injection Over Union，IOU）发展于集合论的雅卡尔指数（Jaccard Index），被用于计算真实边界框Bgt（数据集的标注）以及预测边界框Bp（模型预测结果）的重叠程度。

具体来说，它是两边界框相交部分面积与相并部分面积之比，如下所示：

Python（numpy）代码实现

import numpy as np
def compute_iou(box1, box2, wh=False):
        """
        compute the iou of two boxes.
        Args:
                box1, box2: [xmin, ymin, xmax, ymax] (wh=False) or [xcenter, ycenter, w, h] (wh=True)
                wh: the format of coordinate.
        Return:
                iou: iou of box1 and box2.
        """
        if wh == False:
                xmin1, ymin1, xmax1, ymax1 = box1
                xmin2, ymin2, xmax2, ymax2 = box2
        else:
                xmin1, ymin1 = int(box1[0]-box1[2]/2.0), int(box1[1]-box1[3]/2.0)
                xmax1, ymax1 = int(box1[0]+box1[2]/2.0), int(box1[1]+box1[3]/2.0)
                xmin2, ymin2 = int(box2[0]-box2[2]/2.0), int(box2[1]-box2[3]/2.0)
                xmax2, ymax2 = int(box2[0]+box2[2]/2.0), int(box2[1]+box2[3]/2.0)
 
        ## 获取矩形框交集对应的左上角和右下角的坐标（intersection）
        xx1 = np.max([xmin1, xmin2])
        yy1 = np.max([ymin1, ymin2])
        xx2 = np.min([xmax1, xmax2])
        yy2 = np.min([ymax1, ymax2])
 
        ## 计算两个矩形框面积
        area1 = (xmax1-xmin1) * (ymax1-ymin1) 
        area2 = (xmax2-xmin2) * (ymax2-ymin2)
 
        inter_area = (np.max([0, xx2-xx1])) * (np.max([0, yy2-yy1]))#计算交集面积
        iou = inter_area / (area1+area2-inter_area+1e-6)＃计算交并比
return iou

NMS的python实现

从R-CNN开始，到fast R-CNN，faster R-CNN……都不难看到NMS的身影，且因为实现功能类似，基本的程序都是定型的，这里就分析Faster RCNN的NMS实现：

Python（numpy）代码实现

注意，这里的NMS是单类别的！多类别则只需要在外加一个for循环遍历每个种类即可

def py_cpu_nms(dets, thresh): 
"""Pure Python NMS baseline.""" 
    #dets某个类的框，x1、y1、x2、y2、以及置信度score
    #eg:dets为[[x1,y1,x2,y2,score],[x1,y1,y2,score]……]]
    # thresh是IoU的阈值     
    x1 = dets[:, 0] 
    y1 = dets[:, 1]
    x2 = dets[:, 2] 
    y2 = dets[:, 3] 
    scores = dets[:, 4] 
    #每一个检测框的面积 
    areas = (x2 - x1 + 1) * (y2 - y1 + 1) 
    #按照score置信度降序排序 
    order = scores.argsort()[::-1] 
    keep = [] #保留的结果框集合 
    while order.size > 0: 
        i = order[0] 
        keep.append(i) #保留该类剩余box中得分最高的一个 
        #得到相交区域,左上及右下 
        xx1 = np.maximum(x1[i], x1[order[1:]]) 
        yy1 = np.maximum(y1[i], y1[order[1:]]) 
        xx2 = np.minimum(x2[i], x2[order[1:]]) 
        yy2 = np.minimum(y2[i], y2[order[1:]]) 
        #计算相交的面积,不重叠时面积为0 
        w = np.maximum(0.0, xx2 - xx1 + 1) 
       h = np.maximum(0.0, yy2 - yy1 + 1) 
       inter = w * h 
        #计算IoU：重叠面积 /（面积1+面积2-重叠面积） 
        ovr = inter / (areas[i] + areas[order[1:]] - inter) 
       #保留IoU小于阈值的box 
        inds = np.where(ovr <= thresh)[0] 
        order = order[inds + 1] #因为ovr数组的长度比order数组少一个,所以这里要将所有下标后移一位 
    return keep

NMS的Pytorch实现

在Pytorch中，数据类型从numpy的数组变成了pytorch的tensor，因此具体的实现需要改变写法，但核心思路是不变的。

IoU计算的pytorch源码

# IOU计算
    # 假设box1维度为[N,4]   box2维度为[M,4]
 def iou(self, box1, box2):
        N = box1.size(0)
        M = box2.size(0)
 
        lt = torch.max(  # 左上角的点
            box1[:, :2].unsqueeze(1).expand(N, M, 2),   # [N,2]->[N,1,2]->[N,M,2]
            box2[:, :2].unsqueeze(0).expand(N, M, 2),   # [M,2]->[1,M,2]->[N,M,2]
 )
 
        rb = torch.min(
            box1[:, 2:].unsqueeze(1).expand(N, M, 2),
            box2[:, 2:].unsqueeze(0).expand(N, M, 2),
 )
 
        wh = rb - lt  # [N,M,2]
        wh[wh < 0] = 0   # 两个box没有重叠区域
        inter = wh[:,:,0] * wh[:,:,1]   # [N,M]
 
        area1 = (box1[:,2]-box1[:,0]) * (box1[:,3]-box1[:,1])  # (N,)
        area2 = (box2[:,2]-box2[:,0]) * (box2[:,3]-box2[:,1])  # (M,)
        area1 = area1.unsqueeze(1).expand(N,M)  # (N,M)
        area2 = area2.unsqueeze(0).expand(N,M)  # (N,M)
 
        iou = inter / (area1+area2-inter)
 return iou

其中：

• torch.unsqueeze(1) 表示增加一个维度，增加位置为维度1
• torch.squeeze(1) 表示减少一个维度

NMS的pytorch源码

# NMS算法
    # bboxes维度为[N,4]，scores维度为[N,], 均为tensor
 def nms(self, bboxes, scores, threshold=0.5):
        x1 = bboxes[:,0]
        y1 = bboxes[:,1]
        x2 = bboxes[:,2]
        y2 = bboxes[:,3]
        areas = (x2-x1)*(y2-y1)   # [N,] 每个bbox的面积
        _, order = scores.sort(0, descending=True)    # 降序排列
        keep = []
 while order.numel() > 0:       # torch.numel()返回张量元素个数
 if order.numel() == 1:     # 保留框只剩一个
                i = order.item()
                keep.append(i)
 break
 else:
                i = order[0].item()    # 保留scores最大的那个框box[i]
                keep.append(i)
            # 计算box[i]与其余各框的IOU(思路很好)
            xx1 = x1[order[1:]].clamp(min=x1[i])   # [N-1,]
            yy1 = y1[order[1:]].clamp(min=y1[i])
            xx2 = x2[order[1:]].clamp(max=x2[i])
            yy2 = y2[order[1:]].clamp(max=y2[i])
            inter = (xx2-xx1).clamp(min=0) * (yy2-yy1).clamp(min=0)   # [N-1,]
            iou = inter / (areas[i]+areas[order[1:]]-inter)  # [N-1,]
            idx = (iou <= threshold).nonzero().squeeze() # 注意此时idx为[N-1,] 而order为[N,]
 if idx.numel() == 0:
 break
            order = order[idx+1]  # 修补索引之间的差值
 return torch.LongTensor(keep)   # Pytorch的索引值为LongTensor

其中：

• torch.numel() 表示一个张量总元素的个数
• torch.clamp(min, max) 设置上下限
• tensor.item() 把tensor元素取出作为numpy数字