Long-Tailed Classification

Long-Tailed Classification

长尾(不均衡)分布下的分类问题简介

在传统的分类和识别任务中，训练数据的分布往往都受到了人工的均衡，即不同类别的样本数量无明显差异。一个均衡的数据集固然大大简化了对算法鲁棒性的要求，也一定程度上保障了所得模型的可靠性，但随着关注类别的逐渐增加，维持各个类别之间均衡就将带来指数增长的采集成本。

举个简单的例子，如果要做一个动物分类数据集，猫狗等常见数据可以轻轻松松的采集数以百万张的图片，但是考虑到数据集的均衡，我们必须也给雪豹等罕见动物采集等量的样本，而随着类别稀有度的增加，其采集成本往往成指数增长。

那么如果我们完全不考虑人工均衡，自然的采集所有相关数据呢？这样的数据就是本文所关注的长尾数据。

在自然情况下，数据往往都会呈现如下相同的长尾分布。这种趋势同样出现在从自然科学到社会科学的各个领域各个问题中，参考Zipf's Law或者我们常说的28定律。

直接利用长尾数据来训练的分类和识别系统，往往会对头部数据过拟合，从而在预测时忽略尾部的类别。

用于长尾问题的数据集是训练集imbalance但测试集是balance

如何有效的利用不均衡的长尾数据，来训练出均衡的分类器就是我们所关心的问题，从工业需求上来说，该研究也将大大地提升数据采集的速度并显著降低采集成本

长尾效应主要体现在有监督学习里，无监督/自监督学习等因为不依赖标注，所以长尾效应体现的不明显，目前也缺少这方面的研究（但并不代表无监督/自监督学习不受长尾效应的影响，因为图片本身也有分布，常见的图案和罕见的图案也会形成这样的长尾效应，从而使模型对常见的图案更敏感）。

两种基本方法

长尾分布的最简单的两类基本方法是重采样（re-sampling）和重加权（re-weighting）。这类方法本质都是利用已知的数据集分布，在学习过程中对数据分布进行暴力的hacking，即反向加权，强化尾部类别的学习，抵消长尾效应。

（1）重采样（re-sampling）

• 重采样在早期研究中又包含

  • 对头部类别的欠采样（under-sampling）
  • 对尾部类别的过采样（over-sampling）

• 不过他们的本质其实都是对不同类别的图片采样频率根据样本数量进行反向加权，所以在近年的研究中我们可以统称他们为重采样。其中最常用策略又叫类别均衡采样（class-balanced sampling）。类别均衡的概念主要是区别于传统学习过程中的样本均衡（instance-balanced sampling），也就是每个图片都有相同的概率被选中，不论其类别。而类别均衡采样的核心就是根据不同类别的样本数量，对每个图片的采样频率进行加权。关于采样策略，下面我主要引用Decoupling Representation and Classifier for Long-Tailed Recognition(ICLR 2020)的通用公式来表示：

  \[p_j=\frac{n^q_j}{\sum^C_{i=1}n^q_j} \]

  \(C\)为数据集的类别数量，\(n_i\)为类别\(i\)的样本总数，\(p_j\)为从\(j\)类别中采样一个图片的概率

• 传统的样本均衡采样（instance-balanced sampling）在这个公式里就是\(q=1\)的情况，也就是每个图片等概率被采样，而\(p_{head}>>p_{tail}\)，因为其样本数\(n_{head}\)远远大于\(n_{tail}\)。而狭义的重采样（re-sampling）可以看作\(q\in[0,1)\)的情况，也就是尾部类别的样本图片会比头部类别的图片有更高的概率被采样到。其中类别均衡采样（class-balanced sampling）则是的\(q=0\)情况，即所有类别都采样相同数量的样本，当然尾部类别的图片可能会被反复重复采样，所以一般也会做一些简单的数据增强，例如反转，随机剪裁等。

• 总的来说，重采样就是在已有数据不均衡的情况下，人为的让模型学习时接触到的训练样本是类别均衡的，从而一定程度上减少对头部数据的过拟合。不过由于尾部的少量数据往往被反复学习，缺少足够多的样本差异，不够鲁棒，而头部拥有足够差异的大量数据又往往得不到充分学习，所以重采样也并非是个真正完美的解决方案。

（2）重加权（re-weighting）

• 重加权则主要体现在分类的loss上。不同于采样，因为loss计算的灵活性和方便性，很多比较复杂的任务比如物体检测和实例分割等，都更倾向于使用重加权loss来解决长尾分布问题。毕竟当一张图片上包含多个需要检测或分割的物体，采样时，对他们分别按类别作筛选远比图像层面的采样麻烦的多。而重加权的实现不仅简单，也往往更加灵活。从基于类别分布的反向加权，到不需要知道类别，直接根据分类的可信度进行的困难样本挖掘（Hard Example Mining），如focal loss。 这里我们先给个Re-weighted Cross-Entropy Loss 的通用公式：

  \[loss=-\beta \cdot log\frac{exp(z_j)}{\sum^C_{i=1}exp(z_i)} \]

  其中\(z_i\)是网络输出的\(logit\)，\(\beta\)就是我们重加权中的权重

  • 需要注意的是，这里的\(\beta\)不是一个常数，而是一个取决于具体实现的经过计算的权重，但一般来说\(\beta\)的趋势是，给头部类别更低的权重，给尾部类别更高的权重，从而反向抵消长尾效应。
  • 关于具体的实现，下面会介绍更多最新的较fancy的研究。关于最简单的重加权实现，则可以直接利用公式\(\beta=g(\frac{\sum^C_{i=1}f(n_i)}{f(n_j)})\), \(f(\cdot),g(\cdot)\)可以是任意单调递增函数，比如\(log\)或者各种幂大于0的指数函数。

总的来说，在长尾分类问题中，上述两种方法简单有效，以至于大多数最新的研究其实本质都是对他们的拓展和细化。

2019-2020长尾（不均衡）分布下图片分类问题的研究

主要分为三类：

1. 重采样（re-sampling）相关
2. 重加权（re-weighting）相关
3. 迁移学习（transfer learning）相关

目前在长尾图片分类任务上取得最优结果的两篇论文Decoupling和BBN都是采取了对重采样（re-sampling）技术的改进，并且他们同时发现了一个相似的规律，我觉得对长尾分布乃至任意不均衡分布下识别任务的研究都有着重要的启发（我会在下面详细介绍），所以我个人最看好这类方法。其次，我相对而言也比较喜欢纯粹的重加权（re-weighting）相关的拓展研究，通过对loss的改进来解决长尾/不均衡分布问题，我喜欢这类研究的原因是，他们（大部分）实现简单，往往只需几行代码修改下loss，就可以取得非常有竞争力的结果，因为简单所以很容易运用到一些复杂的任务中。而我个人目前比较不看好的方向，其实反而是各种迁移模型，虽然他们的理念非常好，从头部常见类中学习通用知识，然后迁移到尾部少样本类别中。但是这类方法，往往会需要设计额外的非常复杂的模块，我认为这其实是把简单问题复杂化。简化问题的过程通常是在接近问题本质，可过度复杂的方案则更多的是利用人为的知识去更好的过拟合特定数据。不过我目前的偏好也并非绝对，也许未来就有人可以设计出简单有效的迁移模型。

重采样（re-sampling）相关

Decoupling Representation and Classifier for Long-Tailed Recognition, ICLR 2020

代码：https://github.com/facebookresearch/classifier-balancing

这篇文章应该是目前长尾图片分类领域的SOTA了。该文章和下面的BBN共同发现了一个长尾分类研究的经验性规律：

规律1: 对任何不均衡分类数据集地再平衡本质都应该只是对分类器地再均衡，而不应该用类别的分布改变特征学习时图片特征的分布，或者说图片特征的分布和类别标注的分布，本质上是不耦合的。（当然，这是我自己的总结，原文没这段，也没任何证明）

基于这个规律，Decoupling和BBN提出了两种不同的解决方案，又因为Decoupling的方案更简单，实验更丰富，所以我这里优先介绍Decoupling方法。

Decoupling将长尾分类模型的学习分为了两步

第一步，先不作任何再均衡，而是直接像传统的分类一样，利用原始数据学习一个分类模型（包含特征提取的backbone + 一个全连接分类器）

第二步，将第一步学习的模型中的特征提取backbone的参数固定（不再学习），然后单独接上一个分类器（可以是不同于第一步的分类器），对分类器进行class-balanced sampling学习。

此外作者还发现全连接分类器的weight的norm和对应类别的样本数正相关，也就是说样本数越多的类，weight的模更大，也就导致最终分类时大类的分数（\(logits\)）更高（对头部类的过拟合）。

所以第二步的分类器为归一化分类器，文章中有两种较好的设计：

1. \(\bar{w}_i=\frac{w_i}{\left \| w_i \right \| ^T}\)
2. \(\bar{w}_i=\frac{w_i}{f_i}\)

其中2利用了fixed第一步分类权重\(w_i\)，对每个类学习了一个加权参数\(f_i\)。

Decoupling的核心在于图片特征的分布和类别分布其实不耦合，所以学习backbone的特征提取时不应该用类别的分布去重采样（re-sampling），而应该直接利用原始的数据分布。

Bilateral-Branch Network with Cumulative Learning for Long-Tailed Visual Recognition，CVPR 2020

代码：https://github.com/Megvii-Nanjing/BBN

BBN的核心idea和Decoupling其实是一样的。正因为两个人同时发现了同样的规律，更证明了这个规律的通用性和可靠性。关于上文的规律，BBN做了更详细的分析：

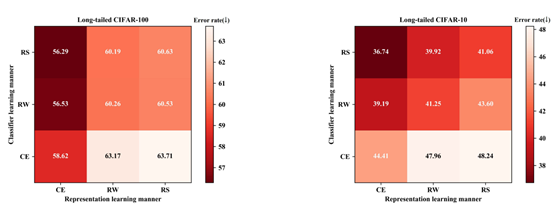
这个图说明，长尾分类的最佳组合来自于：利用Cross-Entropy Loss和原始数据学出来的backbone + 利用Re-sampling学出来的分类器。

和Decoupling的区别在于，BBN将模型两步的学习步骤合并至一个双分支模型。该模型的双分支共享参数，一个分支利用原始数据学习，另一个分支利用重采样学习，然后对这两个分支进行动态加权\((\alpha vs.(1-\alpha))\)。这样随着权重\(\alpha\)的改变，就实现了自然而然地从stage-one到state-two的过度。

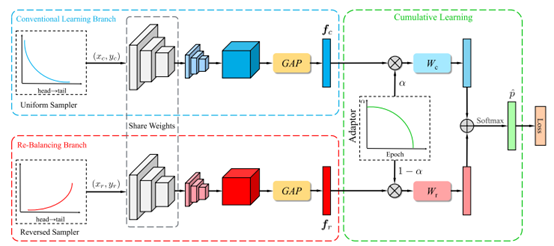
**Dynamic Curriculum Learning for Imbalanced Data Classification，ICCV 2019**

课程学习（Curriculum Learning）是一种模拟人类学习过程的训练策略，旨在从简到难。先用简单的样本学习出一个比较好的初始模型，再学习复杂样本，从而达到一个更优的解。这篇文章的详细分析可以看知乎文章https://zhuanlan.zhihu.com/p/74166778

根据原文的总结，该框架包括两个level的课程学习方案：

1）Sampling Scheduler：调整训练集的数据分布，将采样数据集的样本分布从原先的不平衡调整到后期的平衡状态；

2）Loss Scheduler：调整两个Loss（分类Loss和度量学习Loss）的权重，从一开始倾向于拉大不同类目之间特征的距离（度量学习Loss），到后期倾向于对特征做分类（分类Loss）。

重加权（re-weighting）相关

Class-Balanced Loss Based on Effective Number of Samples，CVPR 2019

代码：https://github.com/richardaecn/class-balanced-loss

这篇文章的核心理念在于，随着样本数量的增加，每个样本带来的收益是显著递减的。所以作者通过理论推导，得到了一个更优的重加权权重的设计，从而取得更好的长尾分类效果。实现上，该方法在Cross-Entropy Loss中对图片根据所属类给予\(\frac{1}{E_n}\)的权重，其中\(E_n=\frac{(1-\beta^n)}{1-\beta}\)代表有效样本数，\(\beta=\frac{N-1}{N}\)，\(n\)是类别总样本，\(N\)则可以看作类别的唯一原型数（unique prototypes)。

Learning Imbalanced Datasets with Label-Distribution-Aware Margin Loss，NIPS 2019

代码：https://github.com/kaidic/LDAM-DRW

这篇文章首先设计了一个如下的非典型的重加权loss。其中\(C\)是常数，\(n_j\)是各类别的样本数。

\[\mathcal{L}_{LDAM}((x,y);f)=-log\frac{e^{z_y-\bigtriangleup _y}}{e^{z_y-\bigtriangleup _y}+\sum_{j\ne y}e^{z_j}} \]

\[where \bigtriangleup_j=\frac{C}{n^{\frac{1}{4}}}_j for j \in{1,...,k} \]

其次，该文章设计了一个两步的训练方法。第一步只利用LDAM loss训练，第二步利用LDAM loss再额外加上传统的re-weighting权重\(n^{-1}_j\)，进一步优化尾部类。这也可以看做规律1的侧面体现。

Rethinking Class-Balanced Methods for Long-Tailed Visual Recognition from a Domain Adaptation Perspective, CVPR 2020

这篇文章对loss的加权分为两项：其一，用上面Class-Balanced Loss Based on Effective Number of Samples的weight作为\(w_{yi}\)，同时，其二，提出了一个条件权重（conditional weight，\(\epsilon_i\))。

\[error=\mathbb{E}_{p_s(x,y)}L(f(x;\theta),y)(w_y+\epsilon _{x,y}) \]

\[\approx \frac{1}{n}\sum^n_{t=1}(w_{y_i}+\epsilon_{x,y})L(f(x_i;\theta,y_i)) \]

而条件权重的学习，则需要再利用Meta-Learning去内部迭代，优化其在一个balanced开发集上的结果。总的来说，idea挺好，但实现上是个偏复杂的方法。由于Meta-Learning的内部迭代，训练也将更费时间费显存。

Remix: Rebalanced Mixup, Arxiv Preprint 2020

Mixup是一个这两年常用的数据增强方法，简单来说就是对两个sample的input image和one-hot label做线性插值，得到一个新数据。实现起来看似简单，但是却非常有效，因为他自带一个很强的约束，就是样本之间的差异变化是线性的，从而优化了特征学习和分类边界。

而Remix其实就是将类别插值的时候，往少样本类的方向偏移了一点，给小样本更大的\(\lambda_y\)。

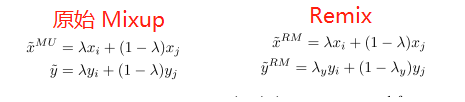
迁移学习（transfer learning）相关

Deep Representation Learning on Long-tailed Data: A Learnable Embedding Augmentation Perspective，CVPR 2020

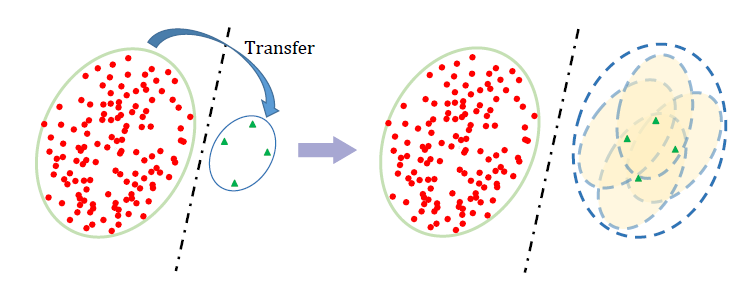
详细分析可以看作者知乎原文（https://zhuanlan.zhihu.com/p/112248291）。简单来说，长尾分布中因为尾部样本缺乏，无法支撑一个较好的分类边界，这篇工作在尾部的样本周围创造了一些虚拟样本，形成一个特征区域而非原先的特征点，即特征云（feature cloud）。而如何从特征点生成特征云，则利用的头部数据的分布。图例如下：

Learning From Multiple Experts: Self-paced Knowledge Distillation for Long-tailed Classification，ECCV 2020

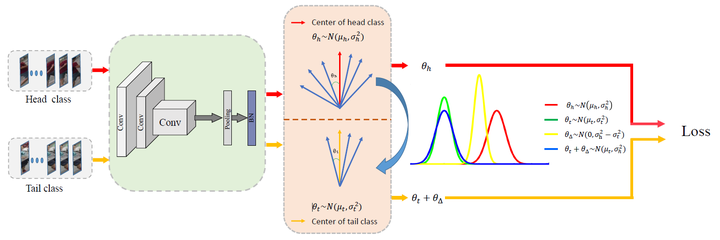
暂且归为迁移学习类。作者发现在一个长尾分布的数据集中，如果我们取一个更均衡的子集来训练，其结果反而比利用完整的数据集效果更好。所以原文利用多个子集来训练更均衡的专家模型来指导一个unified学生模型。

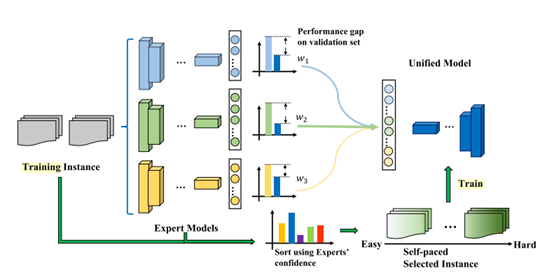
Large-Scale Long-Tailed Recognition in an Open World，CVPR 2019

代码：https://github.com/zhmiao/OpenLongTailRecognition-OLTR

该方法学习一组动态的元向量（dynamic meta-embedding）来将头部的视觉信息知识迁移给尾部类别使用。这组动态元向量之所以可以迁移视觉知识，因为他不仅结合了直接的视觉特征，同时也利用了一组关联的记忆特征（memory feature）。这组记忆特征允许尾部类别通过相似度利用相关的头部信息。

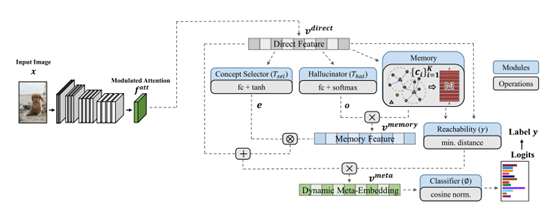
Long-tailed Recognition by Routing Diverse Distribution-Aware Experts, arxiv 2020

代码：https://github.com/frank-xwang/RIDE-LongTailRecognition

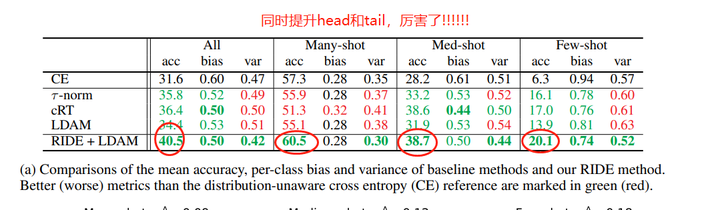
训练多个classifier experts, 然后通过diverse loss让每个classifier有不同的分布（也就是专注于不同的categories）。然后通过一个路由模块，去动态的决定那些classifier expert应该参与分类。虽然看起来是ensemble，但是模型channel缩小了1/4，所以本质上并没有提升计算量。这篇paper证明了基于这种类ensemble的分支结构可以同时提升head和tail的performance。

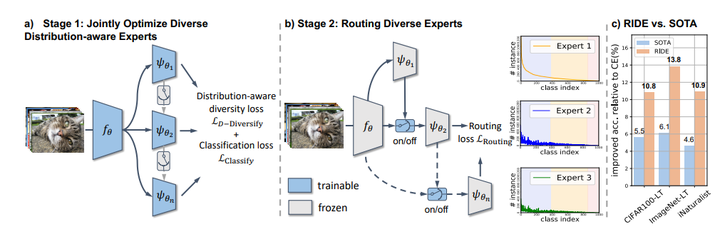
Rethinking the Value of Labels for Improving Class-Imbalanced Learning， Arxiv Preprint 2020

关于如何利用半监督和自监督来解决类别不均衡的问题，因为既然数据的标注难免会遇到类别不均衡的问题，那么如果不利用或少利用类别信息，是否可以解决长尾/不均衡分布问题呢？

因为图片级别的数据易于生成或收集，baseline模型也简单，目前主要的长尾分布研究都集中在图片分类领域。不过随着去年Facebook发布的LVIS（Large Vocabulary Instance Segmentation）数据集（https://arxiv.org/abs/1908.03195），越来越多的人也开始关注起了Instance级别的长尾分布分布问题（物体检测和实例分割），我会在下一节更新这方面的工作。

2019-2020长尾分布下的物体检测和实例分割的研究

长尾（不均衡）分布下的物体检测和实例分割的研究主要发展于2019年LVIS（Large Vocabulary Instance Segmentation）数据集发布之后，所以仍然是个非常“年轻”的领域。如果看LVIS的引用的话就会发现，这个数据集目前总共才40引用不到（by 2020.7.23），所以这里我就不对方法分类了，直接列举目前我所知道的所有研究。其中大部分研究都是重加权的相关算法，即通过设计loss来均衡头尾类别，这主要是因为在物体检测和实例分割中，重采样相关的研究往往实现上会更复杂，收益却更微薄。

Learning to Segment the Tail, CVPR 2020——非重加权的长尾实例分割算法

代码：https://github.com/JoyHuYY1412/LST_LVIS

这篇工作的核心亮点有两处：

第一是把学习长尾分布的数据看成是一种增量学习（incremental learning），即我们是优先学会常见物体（头部数据），然后再基于对常见类别的知识，去认知少见的尾部类别。这其实是一种非常接近人类思维的学习方法。这个工作的学习流程如下图，将类别根据出现频率依次排列，并划分为不同的学习阶段，依次从易到难的学习所有类别。

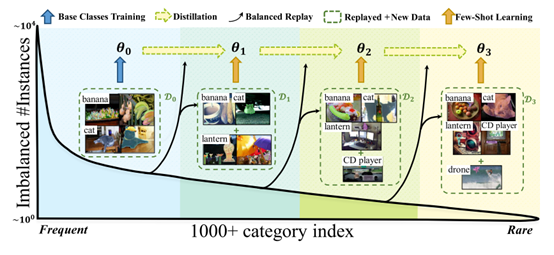
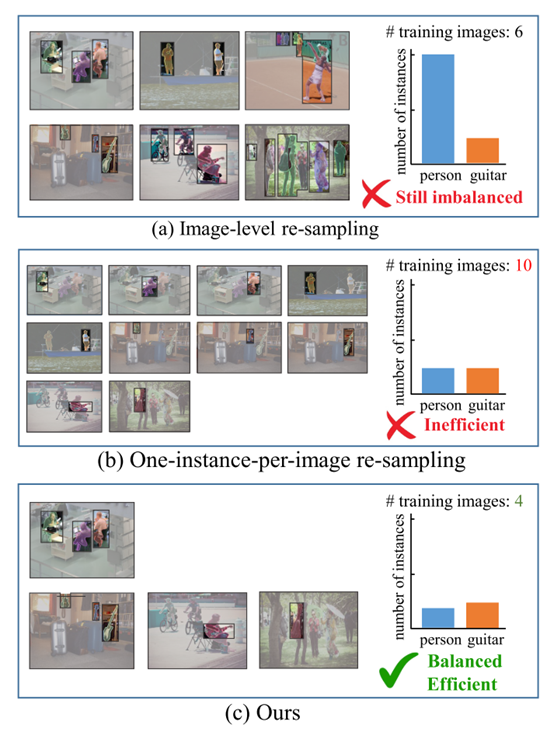
第二个亮点是高效的实例级别重采样（Efficient Instance-level re-sampling）。作为长尾分类的常用方法，重采样在instance-level的数据上却没有重加权来的易于实现。如果一个图片只采样一个实例的话，虽然可以直接将instance-level重采样退化为image-level重采样，但却不够高效。因此基于对数据的观察，我们发现一个物体出现时，往往图片中会同样出现同一类别的其他实例，所以提出了如下高效的实例重采样：

**Focal Loss for Dense Object Detection, ICCV 2017**

代码：https://github.com/clcarwin/focal_loss_pytorch

Focal Loss虽然不是专门用来解决长尾分类的，但是因为其Hard-Example Mining的特性刚好和长尾分类对尾部数据的欠拟合所契合，因此也可以作为长尾物体检测和实例分割的baseline。其实现为如下的FL公式：

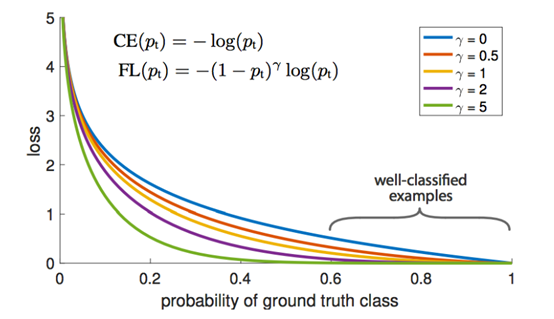
Equalization Loss for Long-Tailed Object Recognition, CVPR 2020

代码：https://github.com/tztztztztz/eql.detectron2

这篇文章是2019年LVIS数据集比赛的冠军。其本质也是一种Re-weighting的算法，通过在计算loss时对尾部类别的加权来实现长尾检测和分割。关于这个研究的详细介绍，可以参考论文原作者的知乎回答：https://www.zhihu.com/question/372070853/answer/1082980270

**Overcoming Classifier Imbalance for Long-tail Object Detection with Balanced Group Softmax, CVPR 2020**

代码：https://github.com/FishYuLi/BalancedGroupSoftmax

这篇也是一个我非常喜欢的工作。该作者和Decoupling的作者同时发现了一个相同的现象，即在长尾分布中分类器参数的模长并不是均匀分布的，而是和类别的出现频率成正相关，即head的类会有更高的模长。这其实也是对头部过拟合的一种体现。

但不同于Decoupling作者直接对模长归一化，本文的作者采用了按模长量级分类，仅对同一量级的类别logits计算softmax，而不是所有类别一起计算softmax。同时不忘对background类做个特殊处理，单独算为一类。

其示意图如下，详细的解读也可以参考知乎回答：https://zhuanlan.zhihu.com/p/158216159

Large-Scale Object Detection in the Wild from Imbalanced Multi-Labels, CVPR 2020

这篇工作也是对softmax做了改进，提出了concurrent softmax，但不同于上文，该工作主要是基于类别间的并发率对loss做了调整。因为传统softmax会在训练时抑制所有非ground-truth类，而当数据不均衡时，很多时候尾部类别很可能是某个头部类别的子类，或者是非常相近的类别，这时候就不该过多的抑制这些类，即便他们不是ground-truth。为了解决这个问题，作者提出了concurrent softmax，对和ground-truth类别有很高并发率（concurrent rate）的类别，给予更少的抑制。concurrent softmax的定义如下：

\[L^*_{cls}(b)=-\sum ^C_{i=1}y_ilog\sigma^*_i \]

\[with \sigma^*_i=\frac{e^{z_i}}{\sum^C_{j=1}(1-y_j)(1-r_{ij})e^{z_j}+e^{z_i}} \]

其中\(r_{ij}\)是从数据中统计出来的类别\(i\)和类别\(j\)的并发率(concurrent rate)：类别\(i\)的物体被标记为\(j\)的概率。

注意该文章并不是在LVIS数据集上做的实验，所以虽然研究的也是长尾分布，但却不能算是同一个setting。

注：本文中作者只是说传统的softmax loss容易使梯度更新时倾向于获得更小的值，没有说明这个与长尾分布有关。相反是后面的soft-balance sampling with hybird training是re-sample的方法

一种崭新的长尾分布下分类问题的通用算法

NeurIPS 2020《Long-Tailed Classification by Keeping the Good and Removing the Bad Momentum Causal Effect》

代码：https://github.com/KaihuaTang/Long-Tailed-Recognition.pytorch

Motivation(研究动机)

这个工作从因果分析的角度，利用一种非常优雅的实现，提出了一种崭新的长尾问题的通用解决思路。而且实现非常简单，能够广泛适用于各种不同类型的任务。之前几期介绍了很多过往的工作，然而有几个问题（缺陷）却一直萦绕在我的脑中没有被解决：

1. 虽然利用数据集分布的re-sampling和re-weighting训练方法可以一定程度上缓解长尾分布的问题。然而这种利用其实是违背现实学习场景的，他们都需要在训练/学习之前，了解“未来”将要看到的数据分布，这显然不符合人类的学习模式，也因此无法适用于各种动态的数据流。
2. 目前长尾分类最优的Decoupling算法依赖于2-stage的分步训练，这显然不符合深度学习end-to-end的训练传统，而论文本身也没有提出让人信服的理由解释为什么特征提取backbone需要在长尾分布下学，而偏偏classifier又需要re-balancing的学。
3. 长尾分布下简单的图片分类问题和其他复杂问题（诸如物体检测和实例分割）研究的割裂，目前长尾分布下图片分类问题的算法日趋复杂，导致很难运用于本来框架就很繁琐的检测分割等任务。而我觉得长尾问题的本质都是相似的，真正的解决方案一定是简洁的，可以通用的。

基于上面这些问题，也就最终诞生了这篇工作。我们提出的De-confound-TDE的优势如下：

1. 我们的训练过程完全不依赖于提前获取的数据分布，只需要在传统训练框架的基础上统计一个特征的移动平均向量，并且这个平均特征在训练中并不会参与梯度计算（只在测试时使用）。这也就解决了传统长尾分类方法依赖“提前获取未来数据分布”的问题。
2. 尽管我们的测试过程和训练过程有所不同，但我们的模型是一次训练到位的，并不需要依赖繁琐的多步训练，这大大简化了拓展至其他任务时的修改成本。
3. 并且，我们成功的将这个方法运用于图片分类（ImageNet-LT，Long-tailed CIFAR-10/-100）和物体检测/实例分割（LVIS dataset）等多个任务，均取得了最优的结果（截止至我们投稿也就是2020年5月）。这证明了我们的方法可以作为继re-balancing之后又一个在长尾数据下通用的Strong Single-Stage Baseline。

Introduction(简介)

我一直觉得大家普遍运用的re-balancing不是一种方法而更像是一个trick，当我决定做这个task时，我follow的Decoupling给了我启发。他的2-stage训练模式让我意识到，re-balancing确实是有问题的，因为他会破坏backbone的特征学习，而必须为此额外增加一个stage来预训练所有的特征提取部分，并且在后续re-balancing学习中freeze住backbone。但既然backbone可以在原始长尾数据上直接训练，classifier真的需要再利用额外的一步训练来balance吗？还是只是目前没有找到对的方法而已呢？

我认为，需要利用原始的长尾分布来学习特征提取的原因在于，大量的尾部类别其实不足以提供足够的样本来学习鲁棒的特征表达，如果强行利用re-balancing trick只会让模型对尾部类别特征过拟合，而对样本充足的头部类别欠拟合。这也不符合人类的认知习惯，人类描述罕见的物体时，往往是通过和已知常见类的比较，比如我会说狮鹫是有着狮子的身体，鹰的翅膀和头的生物，而不必要单独拿一堆狮鹫的图片出来，让你死记硬背住狮鹫的长相。这就解释了为什么直接利用长尾分布的原始数据学习的特征表达器更好，因为他可以充分的利用优质的头部类指导特征学习，可问题在于我们分类时也是直接记住（狮鹫=狮子+鹰），而不需要额外的再去看很多狮鹫样本来和头部的类做“均衡”啊。

于是我想到了自己CVPR 2020的Unbiased Scene Graph Generation工作，可类似的技术却依赖场景图生成本身的复杂网络结构和内部有意义的中间节点。这明显不是个通用的方法，比如图片分类的网络模型除了输入图片和输出的预测，中间层没有任何可解释的意义。近似地使用上述方法也没有明显提升。直到有一天我意识到，机器学习和人类学习的区别既然不在数据，那肯定就在学习方法上了，于是我发现优化器（e.g.，SGD，Adam）本身对网络的学习也有很大的影响，尤其是我发现优化器的动量项时，这货不就是在训练数据时引入数据分布，从而产生shortcut的元凶么。我马上就试了下直接去除动量项，当然这个是不work的，结果非常糟糕。因为动量可以大大提升训练的稳定性，使其更容易收敛到较好的区域，尽管长尾分布下这个较好区域明显倾向于头部类，但也比没有动量的优化结果更好。于是，我们最终决定利用因果分析中的一些思想和技术，尝试在保持动量项的同时，在测试时去除他的影响。这样就可以即利用动量“好的部分”，也剔除了动量“坏的部分”（点题！）。

\[v_t=\underbrace{\mu \cdot v_{t-1}}_{momentum}+g_t \]

\[\theta_t=\theta_{t-1}-l_r\cdot v_t \]

Recipe (快速食用指南)

在介绍本文复杂的因果图构建和后续推导实现，让同学们失去耐心之前，对于想赶紧快速食用我们方法的同学，我给个4步速成指南吧：

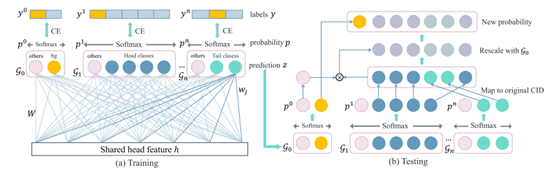
1. 训练时需要De-confound Training，说人话就是classifier需要使用multi-head normalized classifier，即每个类的logits计算如下：\(Y_i=\frac{\tau }{K}\sum^K_{k=1}\frac{(w^k_i)^Tx^k}{(\left \| w^k_i \right \| +\gamma)\left \| x^k \right \| }\)，其中\(\tau ,\gamma\)是超参数，K是multi-head的数量

   分子部分为正常的无bias项的线性分类器，分母部分可以是任何形式的normalization（公式中是我们自己提出的形式，不过事实上如果分母变成 $\left | w^k_i \right |\cdot\left | x^k \right | $ ，也就是cosine classifier也一样work）

2. 同时不要忘记在训练时统计一个移动平均特征\(\bar{x}\)，并将他的单位方向看作是特征对头部类的倾向方向\(\hat{d}=\frac{\bar{x}}{\left \| \bar{x}\right \| }\)

3. 在测试时做counterfactual TDE inference，人话就是从training的logits中剔除我们认为代表对头部类过度倾向的部分，即测试时改用如下公式计算TDE logits：$$TDE(Y_i)=\frac{\tau }{K}\sum^{K_{k=1}\frac{(w}k_i)^Txk}{(\left | w^k_i \right | +\gamma)\left | x^k \right | }-\alpha\cdot \frac{cos(x^k,\hat{d}k)\cdot (w^k_i)T\hat{d}^k}{\left | w^k_i \right | + \gamma}$$详细实现

4. 最后，当运用到诸如物体检测，实例分割的任务中时，还需要对background类做特殊处理，因为background类也是一个头部大类，但是对background的bias却是有益的，因为我们需要依赖他来剔除大量琐碎的细节。其计算方式如下，其中i=0代表background类，\(p_i\)是利用原始training的logits计算出的probability，$q_i是利用TDE logits计算出的softmax后的概率。实现可参考链接中的KEEP_FG部分。

   \[\underset{i\in C}{arg\ max}\begin{cases} (1-p_0)\cdot \frac{q_i}{1-q_0}&i\ne 0\\p_0&i=0\end{cases} \]

   基本只要改classifier，不需要任何额外的训练步骤或复杂的采样算法，是不是很方便。

Causal Graph (因果图构建)

下面就是具体我怎么得出上述的算法。首先，基于我的分析，我们构建了如下的因果图。其中M就是优化器的动量，X是backbone提取的特征，Y是预测。D是特征对头部大类的偏移量。至于为什么会有这个偏移量呢？因为优化器的动量包含了数据集的分布信息，他的动态平均会显著地将优化方向倾向于多数类，这也就造成了模型中的参数会有生成头部类特征的倾向。

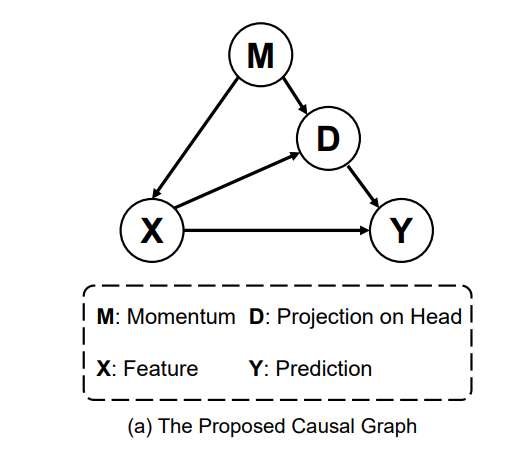
如果对因果图有了解的同学，就会发现这里的M对X和Y是个混淆因子，而D在X-->Y的预测时又会带来中介效应。详细的因果知识背景介绍可以看我一个学弟的知乎文章。我这里简单说下，1）关于混淆因子的概念，最简单的例子是：老年人因为退休了会比年轻人更有时间去保健，而老年人却比年轻人更容易的癌症，即（保健<--年龄-->癌症）。如果不控制年龄的分布，就会得到一个荒谬的结论，保健越多的人得癌症概率越大。这里的年龄就是混淆因子，需要被控制。2）关于中介效应，最简单得例子就是安慰剂效应，即（吃药-->安慰剂效应-->治愈率），如果不剔除安慰剂的中介效应，我们就得不到吃药的真实疗效（吃药-->治愈率）。

De-confound-TDE 算法

因为混淆因子和中介的存在，我们最终期望得到的X对Y的effect其实并不是原始效应（原始logits），而是下图这样的去混杂后的直接效应。其中De-confound training可以在训练中控制M对X的影响，而counterfactual inference的减法，通过类似设置安慰剂对照组的思想，去除了间接效应。

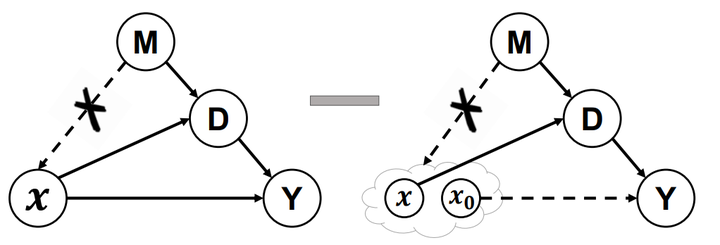
关于我们论文原文的4.1章De-confound training很多同学都觉得有点绕看不懂，其实这一章里公式的承接关系并不是严格的数学推导，而是我们基于因果分析的思想，用数学语言重新定义的工程实现（因为原始的因果分析领域并没有可以直接运用于深度学习的工具）。简单概括为两点：1）由于我们无法统计M的真实分布，因此可以通过multi-head多重采样来近似。2）当我们把原始的logits看成X对Y的因果效应后，我们参考了propensity score的思想，认为这样的effect需要对受控和非受控组（即大类和小类，也就是所有类）做归一化统一分布，最终我们将其实现为一种logits的normalization，其中有包含类别相关与类别不相关两个normalization项。

至于4.2的inference时TDE的减法其实还是比较直接的，我这就不细说了。同时考虑到在一些特殊任务中，有些大类是需要保持合理的倾向性的，比如物体检测和实例分割时，就需要合理地倾向于background类这个大类，否则就会检测到过多无意义地细节。因此我们在4.3中介绍了Background-Exempted Inference这种特殊处理。

How to Understanding TDE (怎么理解TDE)

我们提出的这个因果框架，其实也同时解释了2-stage的方法，并可以将其近似为NDE，关于怎么理解TDE和NDE的区别，可以参考我在补充材料里写的下面这个简单的一维数据二分类例子。

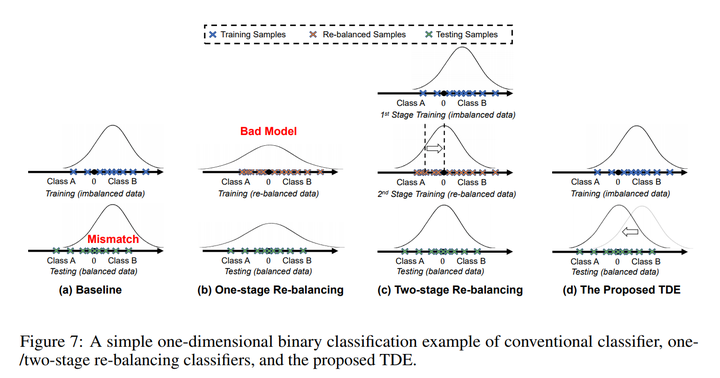
其中高斯曲线代表预测的分布，可以看到传统的直接训练和单步的re-balancing都有严重的问题，而2-stage的方法通过第二步再训练去矫正分类器的分类边界。我们提出的TDE方法则直接通过矫正特征本身的分布来更简单优雅的解决了分布不均衡的问题。

Experiments (实验结果)

我们在ImageNet-LT和Long-tailed CIFAR-10/-100上都超过了之前最优的长尾分布分类算法。

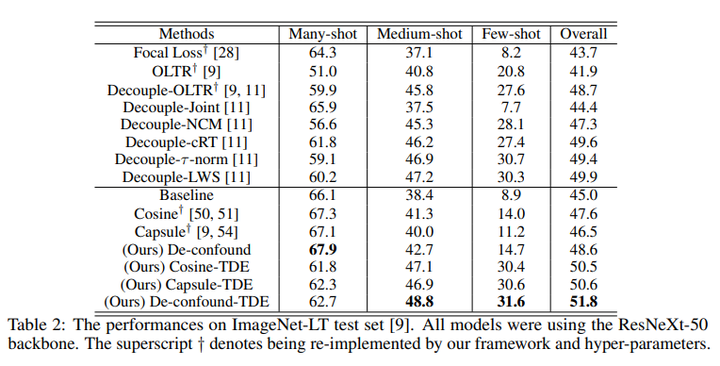
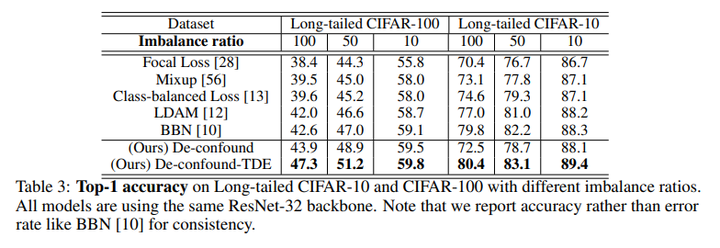
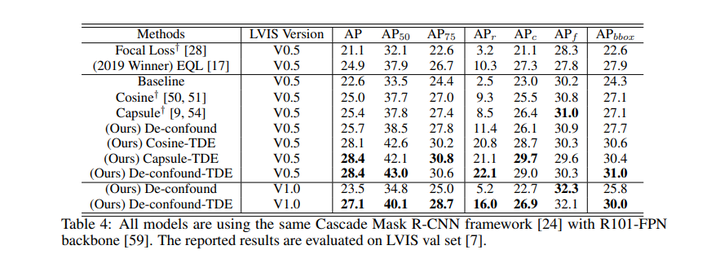
同时我们直接运用到LVIS长尾实例分割数据集下后，我们也超过了去年LVIS 2019比赛的冠军EQL（当然是在相同setting下，比赛正式结果还包含很多比赛专用的trick，比如额外数据，模型融合等）。关于LVIS的实验，比较逗的是，我们paper投出去后，LVIS官方更新了数据集，因此我们最终版也在最新的LVIS V1.0下跑了个结果，方便大家比较。

下面是最有意思的，当我们用Grad-CAM可视化了我们的feature map后我们发现，De-confound-TDE事实上让feature map更紧致了，即更关注少数区分度高的区域，而非整体结构。比如下图中“长牙野猪”的例子，传统的算法关注整个身体，而这部分其实和“猪”这个大类没什么区别，唯一的区别在于“长牙”，而我们的算法则明显的关注到了这些区分度高的紧致区域中了。

总结

单纯从方法上来看，我可不可以这样来理解？

1. decouple两阶段都是在train过程中，一阶段长尾分布下训练representation + classifier；二阶段直接通过暴力resample来调整classifier。

2. de-confound也可以看做两阶段，一阶段在train过程中，通过重采样和normalized的措施来训练representation + classifier；二阶段放在了test过程中，用一阶段中统计的bias来缓解测试中的class bias，得到TDE。