PointNet框架理解

  • 前言：

    • pointnet是点云深度学习的开山之作，最近也有项目是基于此和他的进化版本pointnet++改编的，因此对pointnet的思想和结构进行理解整理。

  • 点云数据：

    • 特性

      • 无序性：只是点而已，排列顺序不影响总体结构
      • 紧密远疏的特性：扫描方法和视角不同导致
      • 非结构化数据：难以直接进行CNN

    • 当下主要需要解决的任务是对点云如何进行特征提取

    • 能不能省略掉预处理操作而直接利用点云呢？

      • 当下深度学习的核心思想就是端到端（end2end）的学习即一条龙服务，PointNet做到了这一点
      graph LR a[点云数据]-->b[PointNet]-->c[object classification] b[PointNet]-->d[object part segmentation] b[PointNet]-->e[semantic scene parsing]

  • PointNet基本出发点

    • 由于点的无序性导致，需要模型具有置换不变性

      \[f(x_{1},x_{2},...,x_{n})\equiv f(x_{\pi_{1}},x_{\pi_{2}},...,x_{\pi_{n}}),x_{i}\in \mathbb{R} ^{D} \]

    • 例如如下公式可以保证置换不变性，但是如何在神经网络中体现出来呢？

      \[f(x_{1},x_{2},...,x_{n})=max{x_{1},x_{2},...,x_{n}} \]

      \[f(x_{1},x_{2},...,x_{n})=x_{1}+x_{2}+...+x_{n} \]

    • 如果直接用Max函数（简单暴力）：

      graph LR a["(1,2,3)"]-->g[g=max] b["(1,1,1)"]-->g[g=max] c["(2,3,2)<br>..."]-->g[g=max] e["(2,3,4)"]-->g[g=max] g[g=max]-->h["(2,3,4)"]

      但是这样会损失太多特征，怎么办？

      所以能不能先升维然后再做MAX操作，其实就是神经网络的隐藏层

    \[f(x_{1},x_{2},...,x_{n})=\gamma \circ g(h(x_{1},...,h(x_{n})) \]

  • 基本模型架构

    • 分别对每个点进行特征提取（卷积或者全连接），再MAX得到全局进行输出

      graph LR a["(1,2,3)"]--"[1*3]*[3*1024]<br>升维"-->a1[MLP]--"[1*1024]<br>变为高维特征"-->g[g=max] b["(1,1,1)"]-->b1[MLP]-->g[g=max] c["(2,3,2)<br>..."]-->c1[MLP<br>...]-->g[g=max] e["(2,3,4)"]-->e1[MLP]-->g[g=max] g[g=max<br>保持置换不变性]--"1024个特征"-->h["γ<br>MLP"]--"权重参数矩阵<br>将1024个特征映射成少量结果"-->i[output]

  • 整体模型架构

    • 分类就是得到整体特征再输出，分割就是各个点特征输出结果

      graph LR a["input points<br>[n*3]"]-->b["mlp(64->64)<br>两个全连接层"]-->c["升维[n*64]"] c["[n*64]<br>升维"]--"分类任务"-->d["mlp(64->128->1024)<br>三个全连接层"]-->e["[n*1024]<br>升维"]-->f[max pool]-->h[1024<br>global feature]-->i["mlp<br>(512,256,k)"]-->j["output scores<br>k"] c["[n*64]<br>升维"]--"分割任务"-->k["[n*1088]<br>[n*64]和n*全局特征进行拼接"] h[1024<br>global feature]-->k["[n*1088]<br>[n*64]和n*全局特征进行拼接"]-->l["mlp<br>(512,256,128)"]-->m["pint feature<br>[n*128]"]-->n["mlp<br>(128,m)"]-->o["output scores<br>[n*m]"]

    • 输入层的n*3中的n需要固定，因为不同的输入点云会具有不同的密度，所以应该对所有输入的数据进行定量采样，方便后期处理

    • [n*1088]拼接特征值的本质是

      graph LR input["[n*64]"]--"由n个[1*64]的点组成"-->a["[1*64]+[1*1024]全局特征"]-->e[n*1088] input["[n*64]"]-->b["[1*64]+[1*1024]"]-->e[n*1088] input["[n*64]"]-->c[...]-->e[n*1] input["[n*64]"]-->d["[1*64]+[1*1024]"]-->e[n*1088]

  • 知识点补充

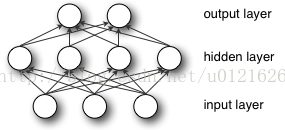
    • MLP（多层感知机，Multilayer Perceptron），也叫人工神经网络（ANN，Artificial Neural Network），除了输入输出层，中间可以有很多隐含层，最简单的MLP只含有一个隐含层，即三层结构：

      img

      从上图可以看到，多层感知机的层与层之间是全连接的（全连接的意思就是：上一层的任何一个神经元与下一层的所有神经元都有连接）。

      多层感知机最底层是输入层，中间是隐藏层，最后是输出层。

      • 输入层没什么好说，你输入什么就是什么，比如输入是一个n维向量，就有n个神经元。

      • 隐藏层主要进行『特征提取』，调整权重让隐藏层的神经单元对某种模式形成反应

        • 隐藏层的神经元怎么得来？

          • 首先它与输入层是全连接的，假设输入层用向量X表示，则隐藏层的输出就是$$f(w_{1}x+b_{1})$$

            \[w_{1}$$是权重，也叫连接系数_ $$b_{1}$$是偏置（阈值）可以排除一些“噪音”的干扰 函数f是激活函数 \]

        • 隐藏层到输出层可以看做是一个多类别的逻辑回归，即softmax回归

        • 整个MLP模型总结起来就是

          \[g(x)=softmax(b_{2}+w_{2}(f(w_{1}x+b_{1}))) \]

        • 对于一个具体的问题，怎么确定这些参数？

          • 求解最佳的参数是一个最优化问题，解决最优化问题，最简单的就是随机梯度下降法了（SGD）：首先随机初始化所有参数，然后迭代地训练，不断地计算梯度和更新参数，直到满足某个条件为止（比如误差足够小、迭代次数足够多时）。

      • 一个例子

        • 目标是识别一个 4 * 3 的黑白图像是0还是1，例子中输入层采用了 12 个神经节点来对应 4 * 3 个像素点，然后隐藏层再使用 3 个神经单元进行特征提取，最后输出层再使用两个神经节点标记识别结果是 0 或 1

          img

          • 输入层

            • 12个神经元对应4*3像素（黑白），如果像素是黑色的，则对应神经元兴奋，否则静息

          • 隐藏层

            • 隐藏层每一个节点会对输入层的兴奋有不同的接收权重，从而更加偏向于某种识别模式

            • 隐藏层第一个神经单元对应下图模式A，也就是对应输入层 4、7号神经单元接收权重比较高，对其他神经单元接受权重比较低，如果超过了神经单元自身的偏置（阈值）则会引发隐藏层的兴奋，向输出层传递兴奋信息，隐藏层其他神经单元同理

              img

          • 各个层如何向上传递信息

            • 根据上边的介绍可知，输入层每个神经单元直接对应原始数据，然后向隐藏层提供信息，隐藏层每个神经单元对不同的输入层神经单元有不同的权重，从而偏向于对某种识别模式兴奋；多个隐藏层的神经单元兴奋后，输出层的神经单元根据不同隐藏层的兴奋加上权重后，给到不同的兴奋度，这个兴奋度就是模型最终识别的结果。

          • 神经网络中权重和偏置的作用

            • 根据上述信息可知，权重会影响神经单元对输入信息敏感程度，比如隐藏层的神经单元通过控制权重形成识别模式偏向，输出层的神经单元调整对隐藏层神经单元的权重，可以形成输出结果的偏向；
              而偏置，可以理解为敏感度，如果没有设置合适的偏置，一些“噪音”就会影响模型识别的结果，或者一些本该被识别出来的场景，但是在传递过程中被屏蔽掉了。

          • 有监督学习下，如何确认权重

            • 在这里需要引入一个概念，『损失函数』又称为代价函数（cost function），计算方法为预测值与学习资料中偏差值之和(误差)的平方，有监督学习就是经过一些『学习资料』的训练，让模型预测的『误差』尽量的小。

              img

    • pooling

      • max pooling

        img

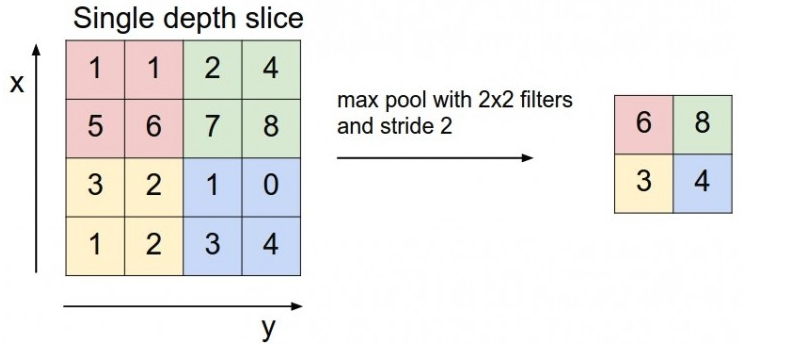
        • 以图片为例，整个图片被不重叠地分割成若干个同样大小的小块（pooling size）。每个小块中只取最大值，舍弃其他节点后，保持原有的平面结构得出output

        • max pooling主要功能是downsampling，却不会损坏识别结果，这意味着卷积后的feature map中有对于识别物体不必要的冗余信息。那么我们就反过来思考，这些 “冗余” 信息是如何产生的。

          直觉上，我们为了探测到某个特定形状的存在，用一个 filter 对整个图片进行逐步扫描。但只有出现了该特定形状的区域所卷积获得的输出才是真正有用的，用该 filter 卷积其他区域得出的数值就可能对该形状是否存在的判定影响较小。 如果不使用 Max pooling，而让网络自己去学习。 网络也会去学习与 Max pooling 近似效果的权重。因为是近似效果，增加了更多的 parameters 的代价，却还不如直接进行 Max pooling。

          Max pooling 还有类似 “选择句” 的功能。假如有两个节点，其中第一个节点会在某些输入情况下最大，那么网络就只在这个节点上流通信息；而另一些输入又会让第二个节点的值最大，那么网络就转而走这个节点的分支。

          但是 Max pooling 也有不好的地方。有些周边信息对某个概念是否存在的判定也有影响。 并且 Max pooling 是对所有的 Feature Maps 进行等价的操作。就好比用相同网孔的渔网打鱼，一定会有漏网之鱼。

        • 对应本文中对点云的max pooling则是

          graph LR e["[n*1024]<br>升维"]-->f[max pool]-->h[1024<br>global feature]
          graph LR input["[n*1024]"]--"由n个[1*1024]的点组成"-->a["1[1*1024]"]--将点按列分解-->e[n*1] input["[n*1024]"]-->b["2[1*1024]"]-->e[n*1] input["[n*1024]"]-->c[...]-->e[n*1] input["[n*1024]"]-->d["n[1*1024]"]-->e[n*1] e[n*1]---f[...]---g[n*1]--"从每一列选择最大值"-->h[1024<br>global feature]
posted @ 2021-09-25 14:41  甫生  阅读(2704)  评论(0)  编辑  收藏  举报