机器学习：线性回归

目录

• 线性回归
  • 线性回归概念
    • 线性回归模型
    • 概率角度解释
  • 正则化方法 (Lasso 回归和岭回归)
  • scikit-learn 线性回归库

线性回归

线性回归概念

线性回归模型

线性回归分析 (Linear Regression Analysis) 是确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法. 即给定一个数据集 \(D={(\mathbf{x}_1,y_1),(\mathbf{x}_2,y_2),\cdots,(\mathbf{x}_N,y_N)}\), 线性回归试图学习到一个线性模型 :

\[f(\mathbf{x}) = \mathbf{\omega}^T \mathbf{x} + b, \ \text{使得} \ \normalsize f(\mathbf{x}_i) \approx y_i \]

即 \(f(\mathbf{x}_i)\) 和 \(y_i\) 之间的距离最小. 可以使用均方误差衡量他们之间的距离, 基于均方误差最小化来进行模型求解的方法称为最小二乘法 (Least Square Method) :

\[(\mathbf{\omega}^*,b^*) = {\arg\min}_{(\mathbf{\omega},b)} \sum^N_i (f(\mathbf{x}_i) - y_i)^2 \]

可以把 \(\mathbf{\omega}\) 和 \(b\) 合并进一个向量形式 \(\hat{\mathbf{\omega}} = (\mathbf{\omega}; b)\), 数据集增加一个维数且最后一个元素恒置 \(1\). 当 \(\mathbf{X}^T\mathbf{X}\) 是满秩矩阵时,

\[\hat{\mathbf{\omega}} = (\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T\mathbf{y} \]

最终得到的线性模型为 :

\[f(\hat{\mathbf{x}}_i) = \hat{\mathbf{x}}^T_i (\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T\mathbf{y} \]

在现实大部分情况, \(\mathbf{X}^T\mathbf{X}\) 不是满秩矩阵, 例如变量数超过样本数时, 最小二乘法的结果不唯一, 可以引入正则项 (regularization term).

概率角度解释

从概率角度来看, 线性回归假设对于给定的 \(y_i\), 可以表示为 \(y_i = f(\mathbf{x}_i) + \varepsilon_i\), 其中 \(\varepsilon_i\) 代表真实值与预测值之间的误差, 并且服从正态分布 \(\varepsilon_i \sim \mathcal{N}(0, \sigma^2)\). 误差的产生有很多种因素的影响, 误差可以看作是这些因素 (随机变量) 之和共同作用而产生的, 由中心极限定理可知随机变量和的分布近似的服从正态分布. 随机变量 \(\varepsilon_i\) 的概率密度函数为 :

\[p(\varepsilon_i) = \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{\varepsilon_i^2}{2\sigma^2}} \]

代入 \(\varepsilon_i = y_i - f(\mathbf{x}_i)\) 有 :

\[p(y_i | \mathbf{x}_i, \mathbf{\omega}) = \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(\mathbf{\omega}^T\mathbf{x}_i - y_i)^2}{2\sigma^2}} \]

利用最大似然估计求解最大化对数似然函数可以得到 :

\[\arg \max _{\mathbf{\omega}} L(\mathbf{\omega}) = \arg \max _{\mathbf{\omega}} \prod^N_i p(y_i | \mathbf{x}_i, \mathbf{\omega}) \]

等价于

\[\arg \max _{\mathbf{\omega}} \mathcal{L}(\mathbf{\omega}) = \arg \max _{\mathbf{\omega}} \log (L(\mathbf{\omega})) = \arg \max _{\mathbf{\omega}} \sum^N_i \log (p(y_i | \mathbf{x}_i, \mathbf{\omega})) \]

最后可以转化为

\[\arg \max _{\mathbf{\omega}} \sum^N_i (f(\mathbf{x}_i) - y_i)^2 \]

也就是均方误差下的损失函数. 最小二乘的意义是所选择的回归模型应该使所有观察值的残差平方和达到最小.

正则化方法 (Lasso 回归和岭回归)

L1 范数正则化和 L2 范数正则化 (分别使用 \(\mathcal{l}_1\text{-norm}\) 和 \(\mathcal{l}_2\text{-norm}\), L2 正则化也被称为 Tikhonov 正则化) 可以看作损失函数的惩罚项. 对于线性回归模型, 使用 L1 正则化的模型叫做 LASSO (The Least Absolute Shrinkage and Selection Operator) 回归 :

\[\begin{equation} \min_\mathbf{\omega}\frac{1}{2N} \sum^N_{i=1} || \mathbf{\omega}^T \mathbf{x}_i - y_i ||^2_2 + \alpha ||\mathbf{\omega}||_1 \end{equation} \label{lasso} \]

使用 L2 正则化的模型叫做岭回归 (Ridge regression) :

\[\begin{equation} \min_\mathbf{\omega} \sum^N_{i=1} || \mathbf{\omega}^T \mathbf{x}_i - y_i ||^2_2 + \alpha ||\mathbf{\omega}||_2^2 \end{equation} \label{ridge} \]

当样本特征很多而样本数相对较少时, 没有加入正则项的模型容易产生过拟合, 也就是模型的抗扰动能力差, L2 正则化可以防止模型过拟合 (overfitting), 它缩小了回归系数, 使得模型相对而言比较稳定. L1 正则化可以产生稀疏权向量, 即产生一个稀疏模型, 可以用于特征选择, 在一定程度上 L1 正则化也有助于降低过拟合风险.

岭回归模型是可微凸函数, 可以直接利用最小二乘等方式求解. 而 LASSO 模型是不可导连续凸函数, 可以使用例如最小角回归 (Least Angle Regression, LARS) 和交替乘子法 (ADMM, Alternating Direction Method of Multipliers) 等方法求解. ADMM 每一步只更新一个变量而固定另外两个变量, 如此交替重复更新, ADMM 算法提供了一个将多优化变量问题转化为单优化变量问题的转化方式, 并未涉及具体的下降方向.

需要注意的是 Lasso 回归比岭回归更容易产生稀疏解, 即通过 Lasso 模型求解的权向量 \(\mathbf{\omega}\) 会有更少的非零分量. Lasso 回归和 Ridge 回归的目标都是最小化损失函数, 式 \(\eqref{lasso}\) 和 \(\eqref{ridge}\) 都是拉格朗日形式, 它们对应的等价形式可以写为:

Lasso 回归:

\[\begin{equation}\left \{ \begin{aligned} & \min_\mathbf{\omega} \frac{1}{2N} \sum^N_{i=1} || \mathbf{\omega}^T \mathbf{x}_i - y_i ||^2_2\\ & \text{subject to } ||\mathbf{\omega}||_1 \leq t \end{aligned} \right. \end{equation} \]

Ridge 回归:

\[\begin{equation}\left \{ \begin{aligned} & \min_\mathbf{\omega} \frac{1}{2N} \sum^N_{i=1} || \mathbf{\omega}^T \mathbf{x}_i - y_i ||^2_2\\ & \text{subject to } ||\mathbf{\omega}||^2_2 \leq t \end{aligned} \right. \end{equation} \]

上面两个模型可以理解为在不同的权向量 \(\mathbf{\omega}\) 限制条件下, 找到目标权向量 \(\hat{\mathbf{\omega}}\) 使得均方误差最小, 其中 \(t\) 可以理解为正则化的力度, \(t\) 越小意味着 \(\lambda\) 越大, 正则化力度越大.

L1 正则化比 L2 正则化更容易得到稀疏解

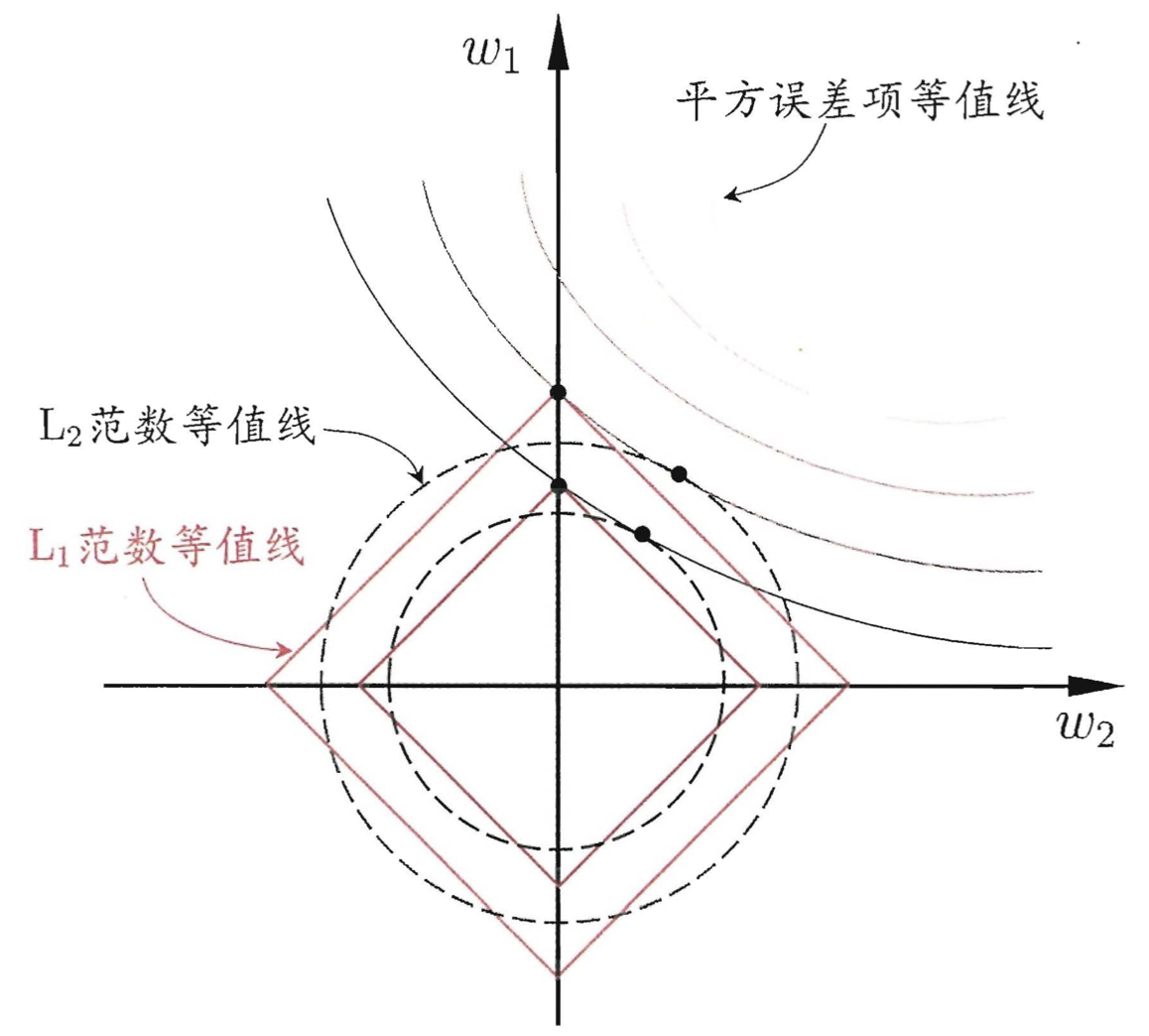
如上图, 假设 \(\mathbf{x}\) 仅有两个属性, 于是权向量 \(\mathbf{\omega}\) 也只有两个分量, 图中的椭圆表示均方误差项的等高线, 再分别绘制出 L1 范数和 L2 范数等高线. 椭圆的中心表示均方误差项取得全局最小的值, 当没有正则项时该值是可以达到的. 但是当有了 L1 正则项或 L2 正则项, 即约束 \(||\mathbf{\omega}||_1 \leq t\) 和 \(||\mathbf{\omega}||_2^2 \leq t\) 时, 权向量 \(\mathbf{\omega}\) 的取值被限制在方形区域或圆形区域以内. 从上图可以看到均方误差项的等高线与方形区域的等高线的切点更有可能在坐标轴上, 而与圆形区域的切点在坐标轴上的概率相对很小. 因此 Lasso 模型更容易使得部分权重为 \(0\), 得到稀疏解.

scikit-learn 线性回归库

Ordinary least squares Linear Regression (普通最小二乘线性回归) sklearn.linear_model.LinearRegression 如下, 没有额外的参数.

class sklearn.linear_model.LinearRegression(*, fit_intercept=True, normalize=False, copy_X=True, n_jobs=None)[source]

Ridge Regression (岭回归) sklearn.linear_model.Ridge 如下, 参数为 \(\alpha\).

class sklearn.linear_model.Ridge(alpha=1.0, *, fit_intercept=True, normalize=False, copy_X=True, max_iter=None, tol=0.001, solver='auto', random_state=None)[source]¶

LASSO Regression sklearn.linear_model.Lasso 如下, 参数为 \(\alpha\).

class sklearn.linear_model.Lasso(alpha=1.0, *, fit_intercept=True, normalize=False, precompute=False, copy_X=True, max_iter=1000, tol=0.0001, warm_start=False, positive=False, random_state=None, selection='cyclic')

ElasticNet sklearn.linear_model.ElasticNet 如下, 它是 L1 范数和 L2 范数的结合, 即:

\[\min_\mathbf{\omega}\frac{1}{2N} \sum^N_{i=1} || \mathbf{\omega}^T \mathbf{x}_i - y_i ||^2_2 + \alpha_1 ||\mathbf{\omega}||_1 + \alpha_2 ||\mathbf{\omega}||_2^2 \]

class sklearn.linear_model.ElasticNet(alpha=1.0, *, l1_ratio=0.5, fit_intercept=True, normalize=False, precompute=False, max_iter=1000, copy_X=True, tol=0.0001, warm_start=False, positive=False, random_state=None, selection='cyclic')

需要注意的是, 当使用普通的线性回归原始数据不需要进行标准化, 这从线性模型的推导表达式可以看出, 每项的系数最后都约减掉了. 但是当加入正则化后需要预先对数据进行标准化, 因为不同尺度的数据大小 (量纲不同) 相当于对其预设了权值, 进而影响权向量的大小, 进而对正则项产生影响. 数据标准化不影响一般的 Logistic 回归 (它也是仅学习权值), 以及决策树及其他一些集成学习算法, 例如 GBDT 和随机森林 (因为它们每次针对一个特征进行处理).