静态时序分析STA
STA目的:
静态时序分析的目的是保证设计中所有的路径,满足内部时序单元对建立时间和保持时间的要求。即无论起点是什么,信号都可以被及时地传递到该路径的终点,并且在电路正常工作所必需的时间段内保持恒定。
STA几个基本概念:
- 信号到达时间(Arrival Time):简称AT,表示实际计算得到的信号到达逻辑电路中某一时序路径终点的绝对时间。它等于信号到达某路径起点的时间加上信号在该路径上的逻辑单元间传递的总和。
- 要求到达时间(Required Arrival Time):简称RAT,表示电路正常工作的时序约束要求信号到达逻辑电路某一路径终点处的绝对时间。
- 时间余量(slack):表示在逻辑电路的某一时序路径终点处,要求到达时间与实际到达时间之间的差(RAT-AT),Slack的值表示该信号到达得是否太晚或太早。太晚意味着该时序电路单元的建立时间不满足,太早则意味着该时序电路单元的保持时间不满足。
- Timing Model:STA 所需要的 Timing Model就存放在标准元件库(Cell Library)中。这些必要的时序资讯是以 Timing Arc(时序弧) 的方式呈现在标准元件库中。Timing Arc 定义逻辑门任两个端点之间的时序关系,其种类有 Combinational Timing Arc、Setup Timing Arc、Hold Timing Arc、Edge Timing Arc、Recovery Timing Arc、Removal Timing Arc、Three State Enable & Disable Timing Arc、Width Timing Arc。
- Combinational Timing Arc:当Timing Arc 相关之特定输出信号变化方向和特定输入(下图A)信号变化方向相反(如输入由0变1,输出由1变0),则此Timing Arc 为inverting sense。反之,输出输入信号变化方向一致的话,则此Timing Arc 为non-inverting sense。当特定输出无法由特定输入单独决定时,此Timing Arc 为non-unate。
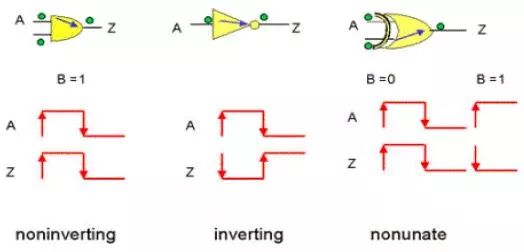
- Setup Timing Arc:定义时序组件所需的Setup Time,依据Clock上升或下降分为2类。
- Hold Timing Arc:定义时序组件所需的 Hold Time,依据Clock 上升或下降分为2类
- Edge Timing Arc:定义时序组件C2q时间,依据Clock上升或下降分为2类。
- Recovery Timing Arc:定义时序组件Clock Active Edge 之前,清除信号不准启动的时间,依据Clock上升或下降分为2类。
- Removal Timing Arc:定义序向组件Clock Active Edge 之后,清除信号不准启动的时间,依据Clock上升或下降分为2类。
- Width Timing Arc:定义信号需维持稳定的最短时间,依据信号维持在0或1的位准分为2类。
5. Timing Constraints:Timing Constraint 为使用者所给定,用来检验设计电路时序的准则。其中最重要的一项就是Clock的描述。对于一个同步电路而言,触发器和触发器之间的路径延迟时间必须小于一个 Clock 周期,也就是说,当我们确认了 Clock 规格,所有暂存器间的路径的 Timing Constraint 就会自动给定了。Clock 规格包含波形、Latency 及 Uncertainty 的定义。波形定义一个Clock的周期及上升沿及下降沿的时间点。Latency 定义从Clock来源到时序单元Clock 输入端的延迟时间。Uncertainty 则定义Clock到时序单元Clock输入端可能早到或晚到的时间。
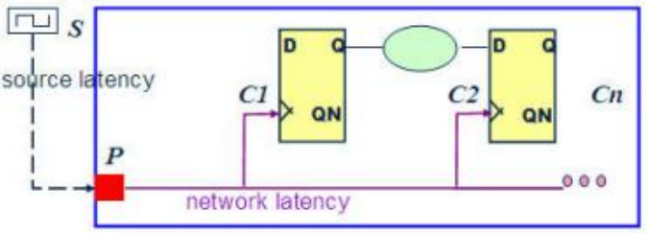
STA步骤:
1、把设计分解为不同的时序路径集合group。
2、计算每条路径的延时信息。
3、检查所有路径的延时,分析时序约束是否可以满足。
路径1:基本输入到内部时序单元的数据输入端
路径2:内部时序单元的时钟输入端到下一个内部时序单元的数据输入端
路径3:内部时序单元的数据输入端到基本输出端口
路径4:基本输入端到基本输出端口
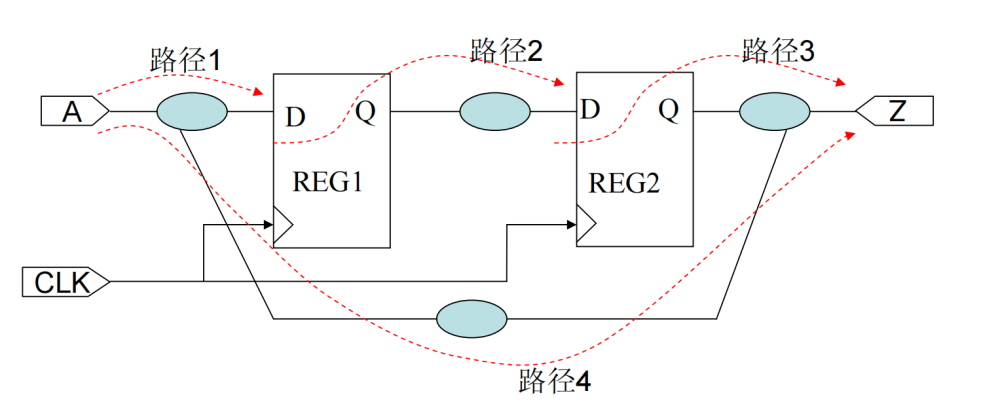
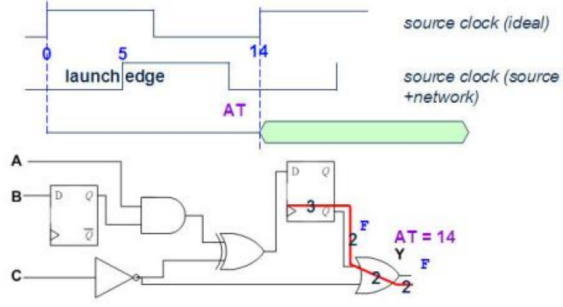
For example: 设计电路如图所示,时序模型(Timing Model)及时序限制(Timing Constraint)如下:
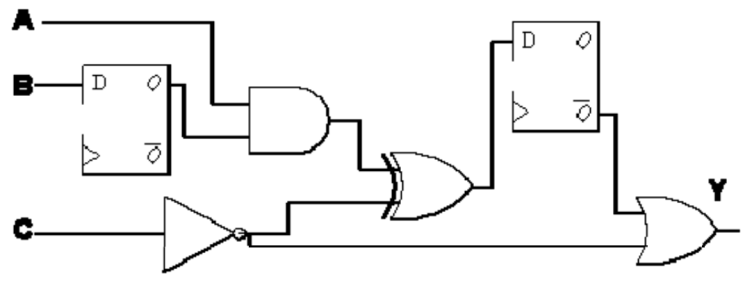
• 所有逻辑门在输出讯号上升时最长的延迟时间为 3ns,最短为 2ns。
• 所有逻辑门在输出讯号下降时最长的延迟时间为 2ns,最短为 1ns。
• 所有连线(Net)最长的延迟时间为 2ns,最短为 1ns。
• 所有 Flip-Flop Clock 到 Q 的延迟时间为 3ns。
• 所有 Flip-Flop 的 Setup Time 为 1ns(Ts)。
• 所有 Flip-Flop 的 Hold Time 为 1ns(Th)。
• Clock 周期为 14ns(Dclkp)。
• Clock source latency 为 2ns(Dclks)。
• Clock network latency 为 3ns(Dclkn)。
• Clock uncertainty 为 1ns(Dclku)。
• A、B、C的 input delay 皆为 1ns(Da、Db、Dc)。
• Y 的 output delay 为 3ns(DY)。
Note:如果输入引脚上的上升沿跳变导致输出引脚电平上升(或不变),而输入引脚上的下降沿跳变导致输出引脚电平下降(或不变),则时序弧为正单边(positive unate)类型,否则为负单边。 例如,与门和或门的时序弧为正单边类型,与非门和或非门的时序弧为负单边类型。
1. 首先找出所有 Timing Path,我们只列出具代表性的 3 条 Timing Path 来加以说明。
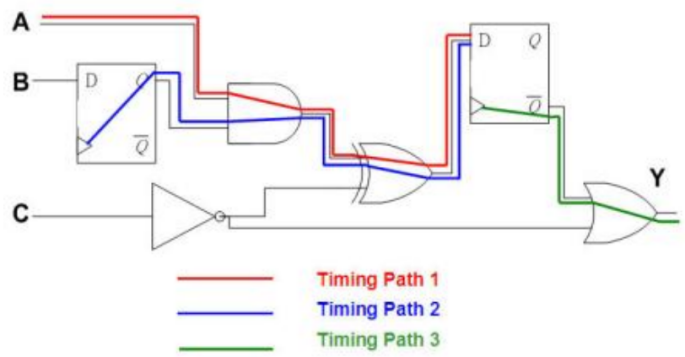
2. 分别假设输入 A 讯号由0变1和由1变0,第1条Path终点讯号到达的时间。
AT(0-1) = Da+2+3+2+3+2=13ns; AT(1-0) = Da+2+2+2+3+2=12ns
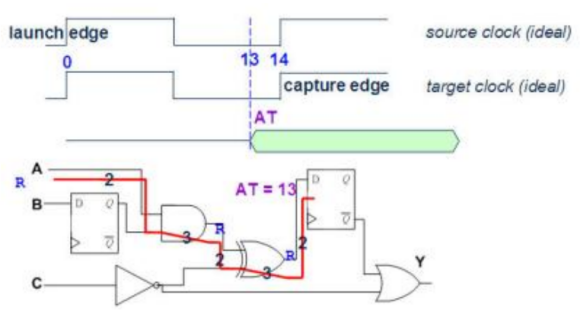
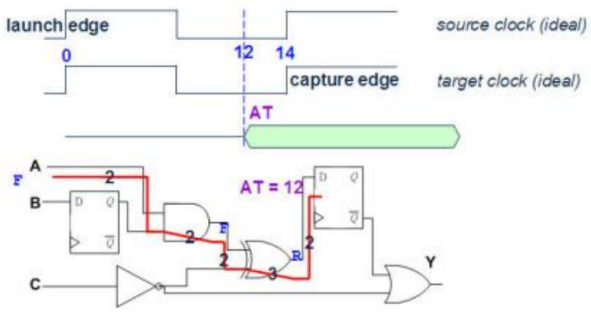
Note: 异或门是非单边时序弧,按最大延迟处理。
3. 计算第1条Path终点的需求时间(Required Time,简称 RT)。
RT=Dclkp+Dclks+Dclkn-Dclku-Ts=14+2+3-1-1=17ns
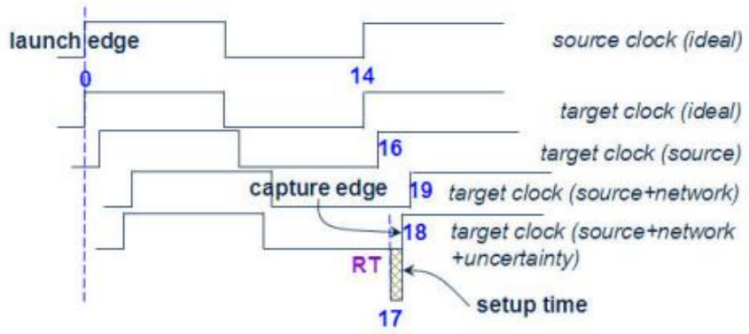
4. 分别假设输入A由0变1,计算第1条Path的Slack。对于Setup Time验证来说等于Slack=RT - AT,对于Hold Time验证来说等于Slack=AT - RT。在此Setup Time范例中,Slack为正,表示讯号实际到达Path终点时间比必须到达的时间还早,因此 Timing 是满足的。
Slack(0-1)=17-13=4ns; Slack(1-0)=17-12=5ns
综合可得,Slack=4ns取较差情况。
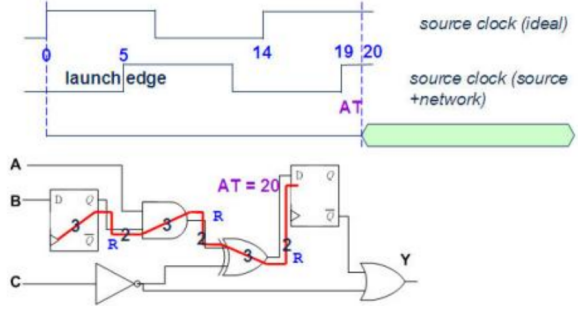
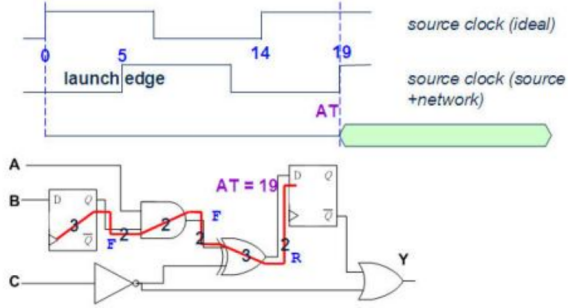
5. 分别假设前级Flip-Flop的讯号由0变1和由1变0,计算第2条Path的AT。
AT(0-1)=Dclks+Dclkn+3+2+3+2+3+2=20ns; AT(1-0)=Dclks+Dclkn+3+2+2+2+3+2=19ns
6. 计算第2条Path的RT
RT=Dclkp+Dclks+Dclkn-Dclku-Ts=14+2+3-1-1=17ns
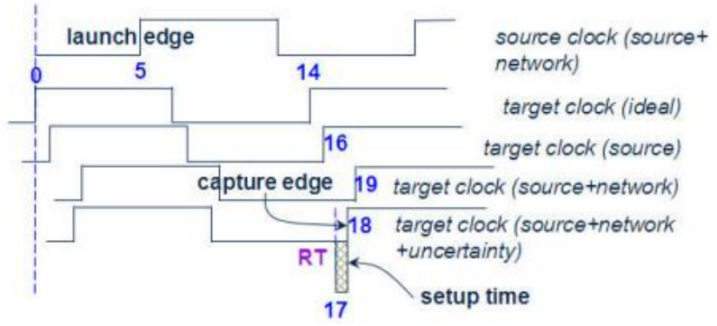
7. 计算第2条Path的Slack,可见不满足Timing
Slack(0-1)=17-20=-3ns; Slack(1-0)=17-19=-2ns
8. 分别假设前级Flip-Flop的讯号由0变1和由1变0,计算第3条的 AT。
AT(0-1)=Dclks+Dclkn+3+2+3+2=15ns; AT(1-0)=Dclks+Dclkn+3+2+2+2=14ns
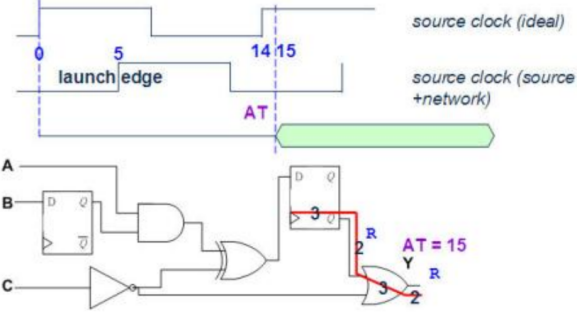
Summary of Computing Slack:
Setup:
- 判断公式:Tcq+Tcomb+Tsetup<=T+Tskew-Tun
- AT = Tcq+Tcomb
- RT=T+Tskew-Tun-Tsetup
- Slack = RT-AT
Hold:
- 判断公式:Tcq+Tcomb>=Thold+Tskew+Tun
- AT = Tcq+Tcomb
- RT = Thold+Tskew+Tun
- Slack = AT-RT


 浙公网安备 33010602011771号
浙公网安备 33010602011771号