三种基于矩的亚像素级边缘定位方法

 1、什么是边缘模型

 

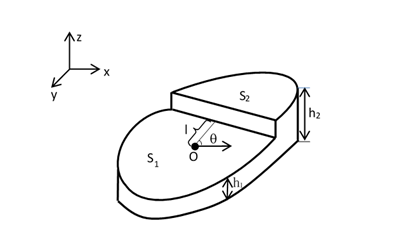
图1.1

        连续二维边缘模型如图1.1所示，其中h₁为背景灰度值，h₂为目标灰度值，l为实际边缘点到原点的归一化距离，θ为边缘法线方向与x轴的夹角，q[-$\pi $/2,$\pi $/2]。

 

2、空间矩法（spatial-gray moment,SGM）

        二阶连续函数f_m(x,y)的p+q阶空间矩定义为

${M_{pq}} = \int\!\!\!\int {x^p}{y^q}{f_m}\left( {x,y} \right)dxdy$

        数字化图像的p+q阶空间矩定义为

${M_{pq}} = \sum \sum {x^p}{y^q}{f_m}\left( {x,y} \right)$

        边缘模型参数计算公式：

\[\left\{ \begin{array}{l}
\theta = \arctan \left( {{M_{01}}/{M_{10}}} \right)\\
l = \left( {4{{M'}_{20}} - {{M'}_{00}}} \right)/\left( {3{{M'}_{10}}} \right)\\
k = \left( {3{{M'}_{10}}} \right)/\left[ {2\sqrt {{{\left( {1 - {l^2}} \right)}^3}} } \right]\\
h = \left[ {2{{M'}_{00}} - k\left( {\pi - 2\arcsin l - 2l\sqrt {1 - {l^2}} } \right)} \right]/2\pi
\end{array} \right.\]

        式中，k为目标灰度和背景灰度的对比度，数值为h1与h2之差，各阶空间矩的数值由各自的矩模板与图像灰度值卷积得到。

 

3、Zernike正交矩法（Zernike orthogonal moment,ZOM）

        二阶连续函数f_m(x,y)的p+q阶的ZOM定义为

${Z_{pq}} = \frac{{p + 1}}{\pi }\int\!\!\!\int f\left( {x,y} \right){V_{pq}}\left( {\rho ,\theta } \right)dxdy$

        边缘模型参数计算公式：

\[\left\{ \begin{array}{l}
\theta = \arctan \left( {\frac{{{\rm{Im}}\left( {{Z_{11}}} \right)}}{{{\rm{Re}}\left( {{Z_{11}}} \right)}}} \right)\\
l = {Z_{20}}/{{Z'}_{11}}\\
k = \left( {3{{Z'}_{11}}} \right)/\left[ {2\sqrt {{{\left( {1 - {l^2}} \right)}^3}} } \right]\\
h = \left[ {{{Z'}_{00}} - k\left( {\pi /2 - \arcsin l - l\sqrt {1 - {l^2}} } \right)} \right]/\pi
\end{array} \right.\]

 

4、正交傅里叶-马林矩法（orthogonal Fourier-Mellin moment,OFMM）

        二阶连续函数f_m(x,y)的p+q阶的OFMM定义为

${\emptyset _{pq}} = \frac{{p + 1}}{\pi }\mathop \sum \limits_{s = 0}^p {\alpha _{ps}}\mathop \int\!\!\!\int \limits_{ - \infty }^{ + \infty } f\left( {x,y} \right){\left( {x + jy} \right)^{\frac{{s - p}}{2}}}{(x - jy)^{\frac{{s + p}}{2}}}dxdy$

        边缘模型参数计算公式：

\[\left\{ \begin{array}{l}
\theta = \arctan \left[ { - \frac{{{\rm{Im}}\left( {2({\phi _{01}} + {\phi _{11}})} \right)}}{{{\rm{Re}}\left( {2({\phi _{01}} + {\phi _{11}})} \right)}}} \right]\\
l = \frac{3}{5}\left( {\frac{{4{\phi _{10}} + {\phi _{20}}}}{{2{{\phi '}_{01}} + {{\phi '}_{11}}}}} \right)\\
k = \left( {2{{\phi '}_{01}} + {{\phi '}_{11}}} \right)/\left[ {2\sqrt {{{\left( {1 - {l^2}} \right)}^3}} } \right]\\
h = \left[ {{{\phi '}_{00}} - k\left( {\arcsin \sqrt {1 - {l^2}} - l\sqrt {1 - {l^2}} } \right)} \right]/\pi
\end{array} \right.\]

        由于OFMM和ZOM法所求的q和l相同，而最终亚像素级边缘定位结果仅仅与q和l有关，因此，OFMM和ZOM法的亚像素级边缘定位结果完全一致，另外三种方法获得的边缘角度q相同。

 

 

 

【 结束 】