相机的标定
相机的标定
在计算机视觉中,为了从图像中提取空间物体的三维几何信息,必须建立图像中像点位置和空间物体表面点三维几何位置的互相对应关系。这种对应关系是由摄像系统成像的几何模型决定的。模型中的参数也就是摄像机的参数,一般的,利用摄像机进行二维或三维的扫描,必须先确定摄像机的参数,在大多数条件下这些参数必须通过实验与计算来确定,而确定这些参数的过程被称为摄像机的标定。
在三维扫描系统中,三维信息是由不同视角采集的灰度图像中获取的。图像是由一个数据阵列表示,其元素值表示了空间某一点的亮度值,该点的空间位置就由假设的摄像机模型和相应的参数确定。摄像机模型是光学成像几何的简化,最简单最常用的是针孔透视模型。但是实际的摄像机成像系统不是理想的针孔透视模型。但是实际的摄像机成像系统不是理想的针孔透视模型,由于加工误差和装配误差,使得物体点在摄像机图像平面实际所成的像与理想成像之间存在光学畸变。因此根据不同的使用场合及所要求的精度,需要建立不同复杂程度的摄像机模型。所建立模型越接近摄像机的实际模型且模型参数能准确地标定出来,则获得的测量精度越高。但与此同时,要求精度越高所需要考虑的因素就越多,模型就越复杂,标定的难度也就越大。本文主要介绍各种摄像机模型及成像原理,摄像机的标定技术和原理,为之后实现符合精度的三维测量系统提供模型选择依据。
一、参考坐标系简介
1、图像坐标系
摄像机采集的数字图像在计算机内可以存储为数组,数组中每一个元素(称为像素,pixel)的值即为图像点的亮度(或者灰度)。如图1.1所示,在图像上定义直角坐标系uv,每一个像素的坐标(u,v)分别是该像素在数组中的列数和行数,所以(u,v)是以像素为单位的图像坐标系坐标。
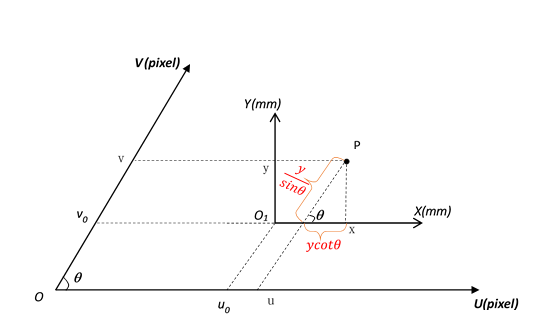
图1.1
2、像平面坐标系
由于像平面坐标系只表示像素位于数组中的列数和行数,并没有用物理单位表示出该图像在像素中的位置,因此需要建立以物理单位(常用mm)表示的理想成像坐标系xy,如图1.1所示。
在本文中,(u,v)表示以像素为单位的图像坐标系坐标,(x,y)表示以物体单位度量的成像平面坐标系的坐标。在(x,y)坐标系中,原点O1定义在摄像机光轴和图像平面的交点处,称为图像的主点(principal point),该点一般位于图像的中心处,但是由于摄像机的制作原因,也许会有少许的偏差。若O1在计算机图像坐标系中坐标为(u0,v0),每一个像素在u轴和v轴方向上的物理尺寸为μx,μy,u轴和v轴的夹角为θ(理想情况下加工时无u,v轴倾斜畸变时,u轴与v轴夹角应该为90o,即θ=90o),图像坐标系任意一点P(u,v)转像平面坐标系为
$\left\{ {\begin{array}{*{20}{c}}{u = {{\rm{u}}_0} + \frac{x}{{{\mu _x}}} - \frac{{ycot\theta }}{{{\mu _x}}}}\\{v = {v_0} + \frac{y}{{{\mu _y}\sin \theta }}}\end{array}} \right.$
其中,
1/mx=(Pixel_x)/(mm)=pixel_x/dpi/25.4
1/my=(Pixel_y)/(mm)=pixel_y/dpi/25.4
(需要先获取设备的DPI,计算mx,my。Pixel/DPI=inch(英寸);Inch*25.4=mm(毫米);)
进而通过其次坐标与矩阵的形式表示为
$\left[ {\begin{array}{*{20}{c}}
u\\
v\\
1
\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}
{\frac{1}{{{\mu _x}}}}&{ - \frac{{cot\theta }}{{{\mu _x}}}}&{{u_0}}\\
0&{\frac{1}{{{\mu _y}sin\theta }}}&{{v_0}}\\
0&0&1
\end{array}} \right]\left[ {\begin{array}{*{20}{c}}
x\\
y\\
1
\end{array}} \right]$
(式2.1)
3、摄像机坐标系
为了分析摄像机成像的几何关系,我们定义一个摄像机坐标系。由图3.1所示,其中O点为摄像机光心,Xc轴和Yc轴与成像平面坐标系的x轴与y轴平行,Zc轴为摄像机的光轴,和像平面坐标系垂直。光轴(Zc)与像平面坐标系的交点为图像的主点(principal point)O1,由点O与Xc、Yc、Zc轴组成的直角坐标系称为摄像机坐标系,OO1为摄像机焦距。

图3.1
4、世界坐标系
选择一个基准坐标系来描述摄像机安放在现实世界的位置,并用它描述世界环境中任何物体的位置,该坐标系就称为世界坐标系,它由基准观测原点和Xw,Yw,Zw轴组成。摄像机坐标系与世界坐标系之间的关系可用旋转矩阵R与平移向量T来描述。因此,假设空间中某一点P在世界坐标系与摄像机坐标系下的其次坐标如果分别是[Xw,Yw,Zw,1]T,[Xc,Yc,Zc,1]T,则存在关系
$\left( {\begin{array}{*{20}{c}}
{{X_c}}\\
{{Y_c}}\\
{{Z_c}}\\
1
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
{{R_{x1}}}& \cdots &{{R_{x3}}}&{{T_x}}\\
\vdots & \ddots & \vdots & \vdots \\
{{R_{z1}}}& \cdots &{{R_{z3}}}&{{T_z}}\\
0&0&0&1
\end{array}} \right)\left( {\begin{array}{*{20}{c}}
{{X_w}}\\
{{Y_w}}\\
{{Z_w}}\\
1
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
R&T\\
{{0^T}}&1
\end{array}} \right)\left( {\begin{array}{*{20}{c}}
{{X_w}}\\
{{Y_w}}\\
{{Z_w}}\\
1
\end{array}} \right) = {M_1}\left( {\begin{array}{*{20}{c}}
{{X_w}}\\
{{Y_w}}\\
{{Z_w}}\\
1
\end{array}} \right)$
式4.1
式4.1中,R为3x3的正交单位矩阵,T=[Tx,Ty,Tz]T为三维平移矩阵。M1是4x4的矩阵,通常称R,T为外部参数,外部参数实际共有6个自由分量,它们是相应于R的三个欧拉角,分别为偏离角θ,倾斜角Φ,旋转角φ,以及相应于T的三个平移分量。R可以用θ,Φ,φ表示,即
${\rm{R}} = \left[ {\begin{array}{*{20}{c}}
{\cos \varphi \cos \theta }&{\sin \varphi \cos {\rm{\theta }}}&{ - \sin \theta }\\
{ - \sin \varphi \cos \phi + \cos \varphi \sin \theta \cos \phi }&{\cos \varphi \cos \phi + \sin \varphi \sin {\rm{\theta }}\sin \phi }&{\cos \theta \sin \phi }\\
{\sin \varphi \cos \phi + \cos \varphi \sin \theta \cos \phi }&{ - \cos \varphi \cos \phi + \sin \varphi \sin {\rm{\theta }}\sin \phi }&{\cos \theta \cos \phi }
\end{array}} \right]$
继续学习请看下一篇博客:相机的标定(2) 摄像机的坐标转换
【 未完待续 ~】


 浙公网安备 33010602011771号
浙公网安备 33010602011771号