最小二乘法的原理及改进

1 最小二乘法

最小二乘使所有点到曲线的方差最小.利用最小二乘对扫描线上的所有数据点进行拟合,得到一条样条曲线,然后逐点计算每一个点Pi到样条曲线的欧拉距离ei（即点到曲线的最短距离）,ε是距离的阈值，事先给定，如果ei≥ε，则将该点判断为噪点.

该方法最重要的事先拟合样条曲线。

 

确定曲线类型的方法：根据已知数据点类型初步确定曲线类型，经验观察初步尝试拟合函数类型.

 

曲线类型选择：直线，二次曲线，三次曲线，对数函数拟合，幂函数拟合，直至方差最小。

直线：f(X₁) = aX₁ + b;

二次曲线：f(X₁) = aX₁² + bX₁ + c;

对数函数：f(X₁) = a + b log(X₁);

幂函数： f(X₁)  = aX₁^b

 

曲线方程参数求解方法：

已知数据点(Xi , Yi)(i = 0,1,2,3…n)；Ø为所有次数不超过n的多项式函数；

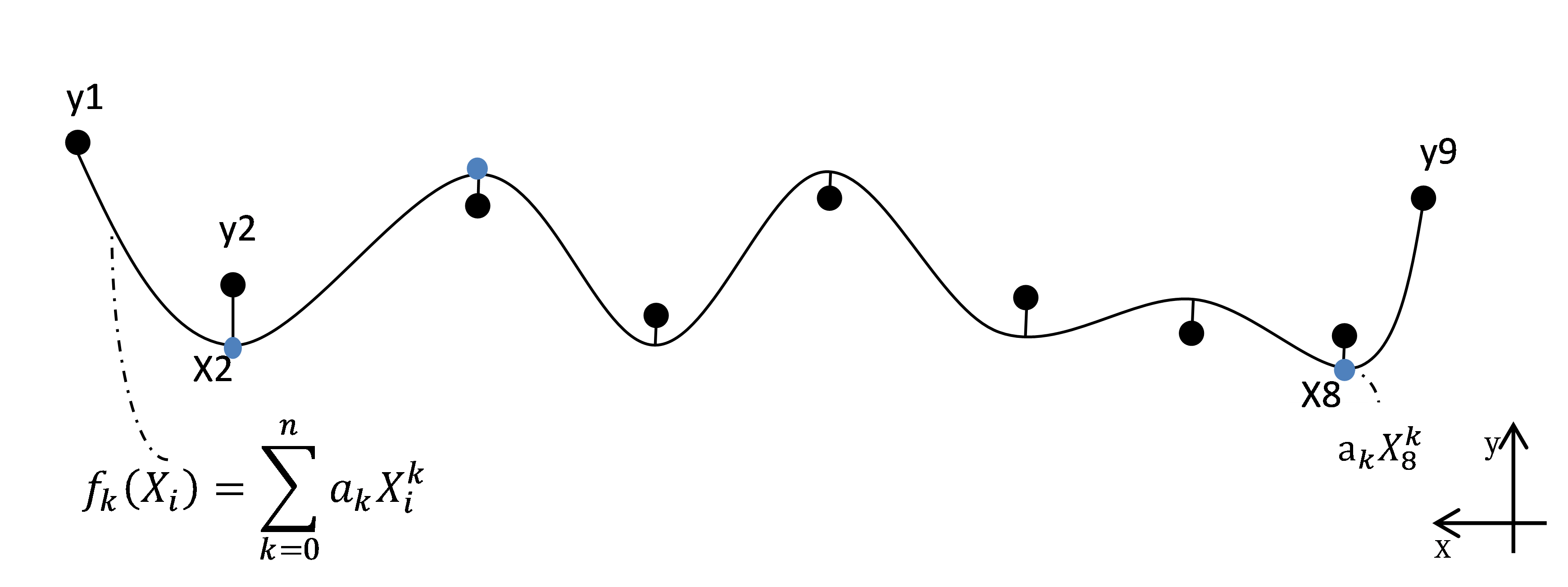
求${f_k}\left( {{X_i}} \right) = \mathop \sum \limits_{k = 0}^n {a_k}X_i^k$(当k=1，为线性拟合，当k>1为多项式拟合)

注：特殊的多项式拟合-非线性拟合方程需先转换为线性方程，

eg：对数函数：f(X₁) = a + b log(X₁)，令log(X₁) = t ,则 f(X₁) = a + b*t，被转化为线性函数，根据t反解X₁；

幂函数： f(X₁)  = aX₁^b ，（假设a为正）等式两边同时转变为对数函数，lg(f(X₁)) = lg(a)+b(lg(X₁)),

令lg(f(X₁))为q, (lg(X₁))为p，则q = lg(a) + b*p，转换为线性关系，解出p，q。

 

以求解${f_k}\left( {{X_i}} \right) = \mathop \sum \limits_{k = 0}^n {a_k}X_i^k \in \emptyset $为例

方差公式：${\rm{min}}\left( {\mathop \sum \limits_{i = 0}^m {{\left( {f\left( {{X_i}} \right) - {Y_i}} \right)}^2}} \right)$，

令

${\rm{I}} = {\rm{\;}}\mathop \sum \limits_{i = 0}^m {\left[ {{f_k}\left( {{X_i}} \right) - {Y_i}} \right]^2} = \;\mathop \sum \limits_{i = 0}^m {\left[ {\mathop \sum \limits_{k = 0}^n ({a_k}X_i^k) - {y_i}} \right]^2} = $min,      （公式1）

公式1存在极小值的必要条件是方程在点Xi处的偏导为零，由此可得，

$\frac{{\partial I}}{{\partial {a_j}}} = 2\mathop \sum \limits_{i = 0}^m \left( {\mathop \sum \limits_{k = 0}^n {a_k}X_i^k - {Y_i}} \right)X_i^j = 0\;\;\;\;\;\;\left( {j = 0,1 \ldots n} \right)$           （公式2）

即：

$\mathop \sum \limits_{k = 0}^n \left( {\mathop \sum \limits_{i = 0}^m X_i^{j + k}} \right){a_k} = \mathop \sum \limits_{i = 0}^m X_i^j{Y_{i\;}}\;\;\;\;\;\;\;\left( {j = 0,1 \ldots n} \right)$          （公式3）

 

将X_i近似为Y_i，由公式3可以求出方程的唯一系数解a_k(k = 0,1,2…n)，从而确定拟合函数，对于多个点需要对系数a_k进行优化，求得满足平均距离最低的系数。

 

2 最小二乘法的优化方法

最小二乘法拟合直线时容易受到个别噪声点的影响，对于个别点需要进行预处理。

 

优化方法：Hough变换直线检测精度分析

标准直线Hough变换（Hough Transform, HT）

标准直线Hough变换采用如下参数化直线方程：

${\rm{xcos\theta }} + {\rm{ysin\theta }} = {\rm{\rho }}$         （公式2.1）

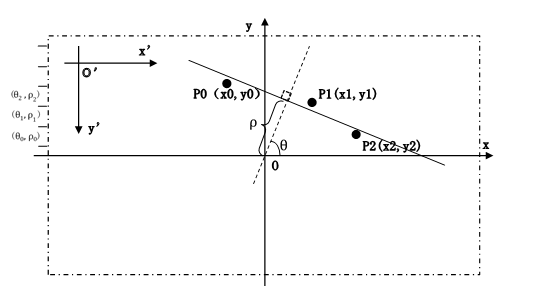
式中，表示直线的法线方向，0≤180，表示原点至直线的距离，其中的单位为像素，的单位为度。通常在图像的直线检测中不使用图像坐标系，而使用原点在图像中心处，y轴方向与图像的y方向相反的正交坐标系。

HT计算过程：

2.1 参数空间投票

为了对直线进行Hough变换，首先需要按一定的量化间隔将可能的与取值范围离散化为若干区间，其中的取值范围规定在[0,180)的区间内，而的取值范围则是由图像矩形的顶点至原点即图像中心的距离确定，整个可能的参数空间被离散化一个二维网格，对每一个可能的离散化参数对（）即每个单元网格设置一个计数器。然后对图像中的每个特征点P0（x0，y0）遍历所有的离散值，如图2所示，对P0点而言共有（P0，P1），（P0，P2）两组值。根据公式2.1计算出，对计算出的参数对（）计数器+1，这个过程被称为参数空间投票。

2.2统计HT找到的直线

当所有的点都完成空间投票后，寻找出参数空间中计数器值大于某一给定阈值T的局部极大点，这些局部极大点对应的直线参数对（）即代表了HT检测到的图像中的直线。

 

HT直线检测分析

由上述计算过程可知，对于给定大小的图像，Hough参数空间的大小主要由的量化间隔或叫分辨率决定。当存在n（特征点个数）个间隔，参数空间（）大小将变为n².所以直线检测的精度会受到点的个数影响，时间也增加到n²。如果设置间隔过大，导致分辨率过低可能存在某些噪点无法被检测到从而影响直线的选择。

 

3 最小二乘法拟合直线的矩阵实现

直线方程可以表示为

y_i = ax_i+b (i = 1,2,3…m)

设a_e,b_e为他们的近似值，令a = a_e+a_ɛ,b = b_e+ b_ɛ,当y作为因变量，x作为自变量时，误差方程为：

\[{{\rm{V}}_{{\rm{yi}}}} = {\rm{\;}}\left[ {\begin{array}{*{20}{c}}
{{x_i}}&1
\end{array}} \right]\left[ {\begin{array}{*{20}{c}}
{{{\rm{a}}_\varepsilon }}\\
{{b_\varepsilon }}
\end{array}} \right] + \left( {{{\rm{a}}_{\rm{e}}}{{\rm{x}}_{\rm{i}}} + {b_e} - {{\rm{y}}_{\rm{i}}}} \right)\]

最小二乘法计算误差：V^TV = min

即  $\mathop \sum \limits_{i = 1}^m {\rm{a}}{{\rm{x}}_{\rm{i}}} + {\rm{b}} - {{\rm{y}}_{\rm{i}}}^2 = min$