Fractal Streets

题目描述

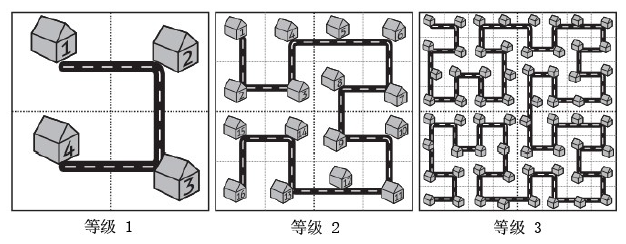
城市的规划在城市建设中是个大问题。不幸的是，很多城市在开始建设的时候并没有很 好的规划，城市规模扩大之后规划不合理的问题就开始显现。而这座名为Fractal 的城市设 想了这样的一个规划方案，如下图所示：

当城区规模扩大之后，Fractal 的解决方案是把和原来城区结构一样的区域按照图中的方 式建设在城市周围，提升城市的等级。对于任意等级的城市，我们把正方形街区从左上角开 始按照道路标号。虽然这个方案很烂，Fractal 规划部门的人员还是想知道，如果城市发展到 了等级N，编号为A 和B 的两个街区的直线距离是多少。街区的距离指的是街区的中心点 之间的距离，每个街区都是边长为10 米的正方形。

输入格式

输入文件包含多组测试数据，第一行有一个整数T 表示测试数据的数目。

每组测试数据包含一行三个整数N, A, B，表示城市等级以及两个街区的编号。

输出格式

对于每组测试数据，在单独的一行内输出答案，四舍五入到整数。

样例输入

3
1 1 2
2 16 1
3 4 33

样例输出

10
30
50

数据范围与约定

对于30% 的数据，N≤5，T≤10。

对于100% 的数据，N≤31，1≤A,B≤2^2N。T≤1000。

 

题解：
　　这道题主要考的是我们的分析能力，关于距离可用勾股定理求。

　　这道题的所有第n等级的城市都跟第n-1座城市有关。

左上：由第n-1级顺时针旋转90度。

左下：左上纵坐标取反。

右上：由n-1级平移。

右下：由n-1级平移。

代码源自算阶，如下：

#include<bits/stdc++.h>
using namespace std;
#define ll long long
pair<ll,ll>calc(ll n,ll m)
{
　　if(n==0) return make_pair(0,0);
　　ll len=1ll<<(n-1),cnt=1ll<<(2*n-2);
　　pair<ll,ll>pos=calc(n-1,m%cnt);
　　ll x=pos.first,y=pos.second;
　　ll z=m/cnt;
　　if(z==0) return make_pair(y,x);
　　if(z==1) return make_pair(x,y+len);
　　if(z==2) return make_pair(x+len,y+len);
　　if(z==3) return make_pair(2*len-y-1,len-x-1);
}
int main()
{
freopen("fra.in","r",stdin);
freopen("fra.out","w",stdout);
　　int t;
　　cin>>t;
　　while(t--)
　　{
　　　　ll n,a,b;
　　　　cin>>n>>a>>b;
　　　　pair<ll,ll> x=calc(n,a-1);
　　　　pair<ll,ll> y=calc(n,b-1);
　　　　ll dx=x.first-y.first,dy=x.second-y.second;
　　　　double ans=(sqrt(dx*dx+dy*dy)*10);
　　　　printf("%0.lf\n",ans);
　　}
　　return 0;
}

　　❀完结撒花❀