现在最大的问题是,我们编写一个找到起点到终点的最短路径的程序?要做到这一点,我们先给单元格命名,
我们有6列 命名为0到5和5行 从0到4.我的思路是保存一个想要进一步調查的列表,或者在搜索中我们称其为展开,让我们把这个列表称作open. 一开始我们的列表上只有一个位于【0,0】上的状态,我的初始状态。
为了确保我不会再选择这个状态——我不希望在我的路径上有任何循环,让我用红色的小勾把它标记出来,
我现在可以检测这个状态是不是我的目标状态。显然不是,我还没有进行任何规划,我下面要做的就是展开这个状态,我把它从open表上拿走,然后看看所有的继任者,现在这里有两个,【1,0】【0,1】,现在已经展开的,让我来检测一下,最后一个我要做的事情是open列表中的每一个状态,分别需要展开多少次?
这里是0,这两个是1,用红色写出来。这就是所谓的g值。
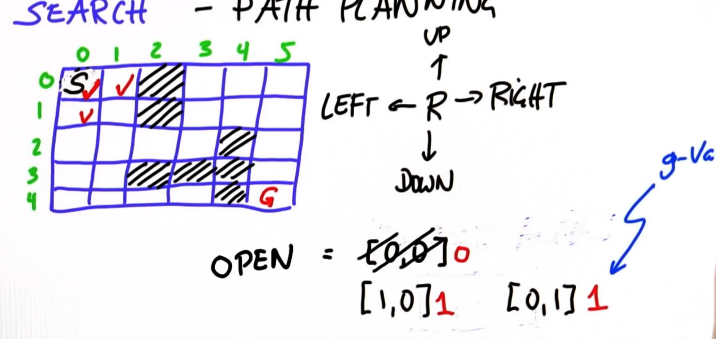
当我规划完成后,这将是最优的路径长度,现在让我们更进一步展开两个中的一个,我们总是展开一个具有最小的g值的,但上面连个是相等的,都是1.让我们展开左边这一个,他有三个邻居,【0,0】【1,1】【2,0】
但是【0,0】已经关闭,我们不考虑,于是就只有【2,0】【1,1】.现在这两个都有一个为2的g值,我们给他们搭上勾,现在我要做的 是在open列表中找的g值最小的节点。恰好是【0,1】,他的g值是1.
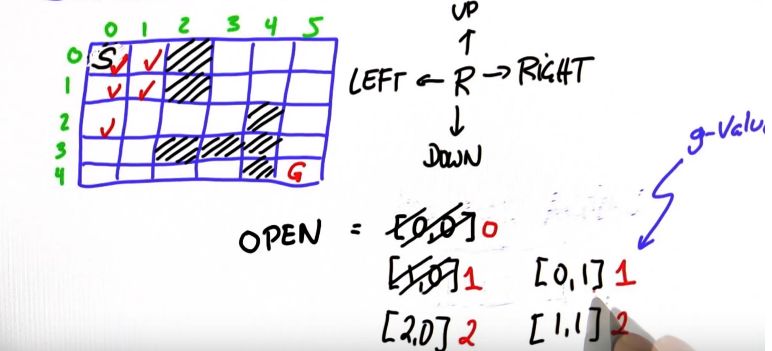
他有两个邻居,【0,0】【1,1】,但是两个都标记过了。因此在这里存在在展开。
我只展开那些未标记过的节点,现在open表中有两个节点,如果接下来我们的节点在自由空间上展开,直到到达我们的目标节点,无需证明当我们到达目标节点的时候g值刚好就是起点到终点的步数。这里的秘诀是
我总是展开最小的g值节点。现在要做的就是写一段实现代码。
这是我们的网格,你可以看到1是障碍网格。

init=[0,0] 是起始点,目标点是【4,5】
就是goal=[len(grid)-1,len(grid[0])-1]
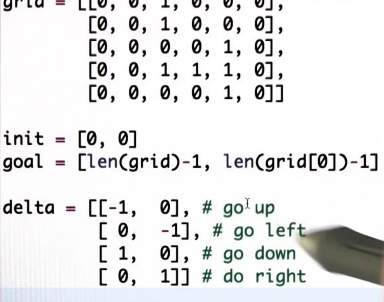
我也将需要用到的4种运动写在一个称为delta的列表中,所以当你在搜索继任者时,你可以依照这顺序,
第一个是往上,从这个维度减1,第二个往左,第三个往下,第四个往右。
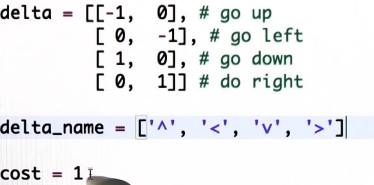
现在每一步的花费都是1.现在要做的是编写代码,按这个格式输出3个值,第一个是g值,其他两个是坐标x和y.然后找出列表中最小的g值的元素。

再展开——网格单元【0,0】展开到【1,0】【0,1】,两者的g值都递增了1.
然后再次在这些条目中找出具有最小的g值的一个

这个列表中只有一个【1,1】,还没有标记,他获得的2的g值。
现在再次删除具有最小g值的元素,就是第一个,然后产生一个新的列表 new open list.
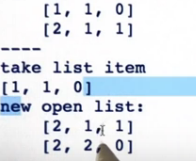
通过这种方式不断执行。你就可以看得g值继续递增,直到到7.

最后,当g值变为11,应该展开节点【3,5】
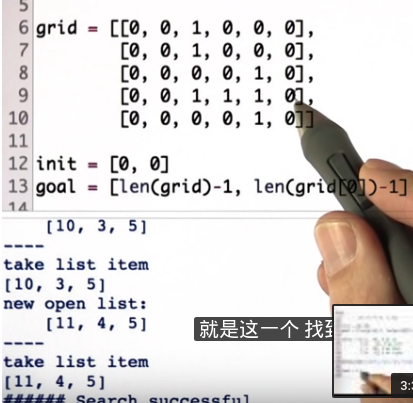
就是这个未被标记的邻居。就是【4,5】,g值为11.
现在你要编写的代码只有输出这三个。【11,4,5】
# in the form of [optimal path length, row, col]. For # the grid shown below, your function should output # [11, 4, 5]. # # If there is no valid path from the start point # to the goal, your function should return the string # 'fail' # ---------- # Grid format: # 0 = Navigable space # 1 = Occupied space grid = [[0, 0, 1, 0, 0, 0], [0, 0, 1, 0, 0, 0], [0, 0, 0, 0, 1, 0], [0, 0, 1, 1, 1, 0], [0, 0, 0, 0, 1, 0]] init = [0, 0] goal = [len(grid)-1, len(grid[0])-1] cost = 1 delta = [[-1, 0], # go up [ 0,-1], # go left [ 1, 0], # go down [ 0, 1]] # go right delta_name = ['^', '<', 'v', '>'] def search(grid,init,goal,cost): # ---------------------------------------- # insert code here # ---------------------------------------- return path
这是我的解决方案 - 我定义了一个函数“search”,这是我将要在最后运行的唯一函数。这就像主要的程序。
要检查单元格扩展后的状态,以便我们不再扩展它们,我将一个名为“closed”的数组定义为与我的网格相同的大小,
它有两个值,0和1--0,它仍然是开放的,1表示它正在关闭。你也可以使用布尔值。
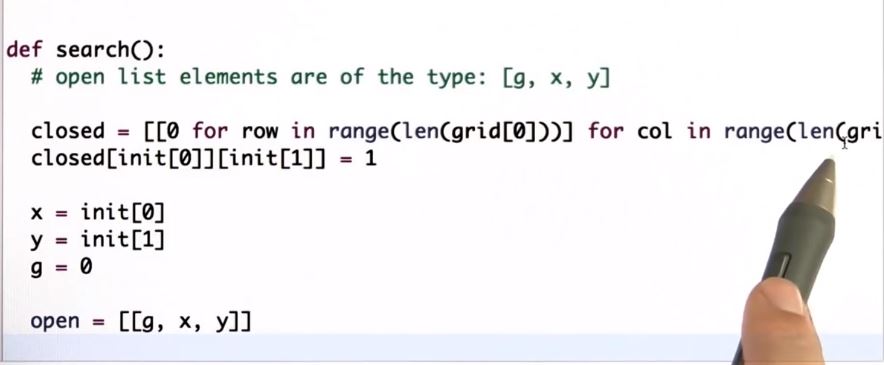
def search():
closed=[[0 for row in range(len(grid[0]))] for col in range(len(grid))] #有问题
closed[init[0]][init[1]]=1
x=init[0]
y=init[1]
g=0
open=[[g,x,y]]
found=False #flag that is set when search complete
resign=False #flag set if we can not find expand
while found is False and resign is False:
if len(open)==0
resign=True
print 'fail'
else:
open.sort()
open.reverse()
next=open.pop()
x=next[1]
y=next[2]
g=next[0]
if x==goal[0] and y==goal[1]:
found=True
print next
else:
for i in range(len(dalta)):
x2=x+delta[i][0]
y2=y+delta[i][1]
if x2>=0 and x2<len(grid) and y2>=0 and y2<len(grid[0]):
if closed[x2][y2]==0 and grid[x2][y2]==0:
g2=g+cost
open.append([g2,x2,y2])
closed[x2][y2]=1



 浙公网安备 33010602011771号
浙公网安备 33010602011771号