高斯分布

为了了解无人驾驶的不确定性，你至少需要掌握高斯分布的基础知识。例如，在研究传感器数据的不确定性或是确定行人的位置时，往往会应用高斯分布。

接下来，本课程将简要介绍高斯分布和它的起源。

然而，这并不是一门纯统计课程。我们只是对这种分布进行简单介绍，同时假设你已经熟悉了平均值、标准差、总体和样本等术语，其中：

总体指全部数据点的集合。例如，当你在测量人们的体重时，总体便是世界上的全部人口。
样本指总体中的一部分。在上面体重的例子中，测量世界上所有人的体重并不现实，因此你也许会从总体中随机选择样本。
均值指平均值。在上面这个例子中它指全部人口的平均体重。
标准差能测量数据的分布。这组数据是趋于围绕平均值分布，还是趋于离散？

如果你并不熟悉这些术语，或是需要复习，这些资源对你来说也许有用：样本 vs 总体。

高斯分布

现在我们来直接看看高斯分布，接下来我们会探讨高斯分布究竟是什么，它与无人驾驶又有什么渊源。

你也许认识这个形状，它通常被称作钟形曲线。请注意，与均匀连续分布一样， y 轴上写着“概率密度函数”。

当前， x 轴上写着 “x 值”，但它可以表示任何连续变量，如温度、高度或速度。

高斯方程

尽管这条曲线看上去难以绘制，但有一个方程可以在 x 变量和 y 变量之间建立映射关系。下面是高斯分布的概率密度函数：

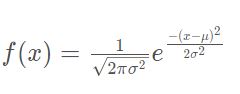
这个方程似乎有些复杂，所以在本节课的下一部分，我们会把它拆分开来。

符号 $\muμ 表示总体均值。符号 \sigmaσ 则是分布标准差，能表示分布状况。如果你还记得统计学里的内容，总体的均值和标准差都是恒定的。对于特定的总体， x 是唯一的变量。$

示例

让我们更具体一些。假设你正在研究与旧金山冬季气温相关的概率，并且每日最低气温遵循高斯分布。当然，如果你实地测量当地的冬季气温，结果也许并非如此，但在这个例子里我们先这样假设。

再假设旧金山冬季平均最低气温是 50 华氏度。换句话说，如果你在整个冬季每天都测量最低气温的话，平均值将会是 50 华氏度。我们再把标准差定在 10 华氏度。

现在，我们把均值和标准差带入高斯方程，会得到下面这个等式：

在把均值和标准差代入之后，这个方程看上去是不是简单多了？你可以任意取 x 值，在这个例子里，它代表温度，接着你可以计算出每个 x 值对应的 y 值。

均值

均值在高斯分布中究竟代表什么？它实际上是钟形曲线的中心点。

回到刚才旧金山气温的例子，下边的图像表示了在三个不同均值下的三种分布。其他数值保持不变，包括标准差。

我们可以发现，在其他数值恒定的情况下，改变均值会使曲线左右移动。

标准差

标准差在高斯分布中起了什么作用？让我们重复刚才的实验，看看在其他数值保持恒定的情况下，改变标准差会发生什么。

当标准差增加时，不确定性也增加了。比较一下标准差为 5 和 15 时的图像，当标准差为 5 时，分布看起来更窄更高，这意味着此时温度更接近 50 度。

当标准差增加到 15 时，分布变得更宽更平，此时温度接近 50 度的概率下降，而温度数值沿着 x 轴向左或向右移动的概率变高。

曲线下方的面积

作为提示，连续概率分布中的 y 轴代表了概率密度方程。x 轴表示一个连续变量，比如重量、速度，等等。作为参考，下方是我们之前看过的均值为 50、标准差为 10 的高斯分布。

但 y 轴上的概率密度函数并不是概率的直接测量结果。概率密度函数下方的面积表示概率。

比如，假设你想知道温度在45 华氏度和 60 华氏度之间的概率，你需要计算温度在 45 度到 60 度时曲线下方的面积。

Area Under the Curve from 45 to 60

高斯概率密度方程下方的面积

然而，你应当如何计算像高斯分布这样的曲线下方的面积呢？如果你熟悉微积分，曲线下方的面积实际上被称为一个积分。然而，计算高斯概率密度函数的积分并不轻松。

因此，你可以使用标准正态表。这个表格中包含了计算高斯概率密度函数下方面积所需要的数据。这一表格的使用方法并不在本课程的讨论范围内，它通常在统计导论课程中进行介绍，比如优达学城的统计学入门。

幸运的是，Python 拥有一个库，可以计算高斯概率密度函数下方的面积。

曲线下面积

你将使用Python来计算与高斯分布相关的概率。换句话说，你将学习如何计算概率密度函数下的面积。

SciPy库

Python有一个名为SciPy的库，用于运行科学运算与数学计算。你将要特别使用到实现高斯分布的库的一部分。

示例：概率密度函数

下面的代码单元格用两种方法来计算高斯概率密度函数。首先，我们将使用前面练习中的密度函数。然后，我们将使用SciPy库的实现对结果进行比较。

你会看到结果是完全一样的。

from scipy.stats import norm
import numpy as np

# our solution to calculate the probability density function
def gaussian_density(x, mu, sigma):
    return (1/np.sqrt(2*np.pi*np.power(sigma, 2.))) * np.exp(-np.power(x - mu, 2.) / (2 * np.power(sigma, 2.)))

print("Probability density function our solution: mu = 50, sigma = 10, x = 50")
print(gaussian_density(50, 50, 10))
print("\nProbability density function SciPy: mu = 50, sigma = 10, x = 50")
print(norm(loc = 50, scale = 10).pdf(50))

你可能想知道为什么高斯分布在SciPy库中被称为“norm” ，这是因为高斯分布也称为正态分布。

此外，请注意，要初始化分配，loc关键字是平均值，scale关键字是标准差。

计算概率

概率密度函数下的面积表示概率。你的任务是编写一个用于计算两个x值之间的概率的函数。例如，使用旧金山冬季气温的例子，气温在30度到50度之间的概率是多少？

SciPy库有一个函数，可以帮你计算曲线下方的面积。它被称为cdf (cumulative density function)。你可以使用与pdf方法类似的cdf SciPy方法。运行下面的代码单元格，查看示例。

norm(loc = 50, scale = 10).cdf(50)

　　0.5

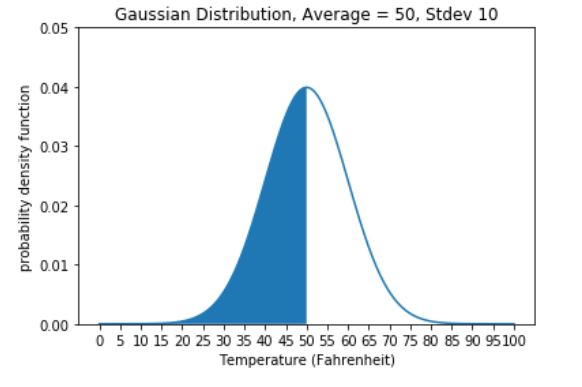
为什么输出值是0.5？通过cdf方法，你可以根据输入值，得出从x = 负无穷大到曲线下方的面积，在这种情况下，输入值是50。曲线下方面积为0.5，表示气温介于负无穷大到50度之间的概率为50％。

运行下面的代码单元格，查看从负无穷大到50的曲线下方的面积的可视化。

import matplotlib.pyplot as plt
%matplotlib inline  

### 
# The plot_fill function plots a probability density function and also
# shades the area under the curve between x_prob_min and x_prob_max.
# INPUTS:
# x: x-axis values for plotting
# x_prob_min: minimum x-value for shading the visualization
# x_prob_max: maximum x-value for shading the visualization
# y_lim: the highest y-value to show on the y-axis
# title: visualization title
#
# OUTPUTS:
# prints out a visualization
### 

def plot_fill(x, x_prob_min, x_prob_max, y_lim, title):
    # Calculate y values of the probability density function
    # Note that the pdf method can accept an array of values from numpy linspace.
    y = norm(loc = 50, scale = 10).pdf(x)
    
    # Calculate values for filling the area under the curve
    x_fill = np.linspace(x_prob_min, x_prob_max, 1000)
    y_fill = norm(loc = 50, scale = 10).pdf(x_fill)
    
    # Plot the results
    plt.plot(x, y)
    plt.fill_between(x_fill, y_fill)
    plt.title(title)
    plt.ylim(0, y_lim)
    plt.xticks(np.linspace(0, 100, 21))
    plt.xlabel('Temperature (Fahrenheit)')
    plt.ylabel('probability density function')
    plt.show()

average = 50
stdev = 10
y_lim = 0.05
x = np.linspace(0, 100, 1000)

plot_fill(x, 0, 50, y_lim,
          'Gaussian Distribution, Average = ' + str(average) + ', Stdev ' + str(stdev))

练习

如果你想知道气温在25到75之间的概率，该怎么办？根据你目前看到的内容，你可以根据获得所有需要的信息，编写一个用于做这个计算的函数。

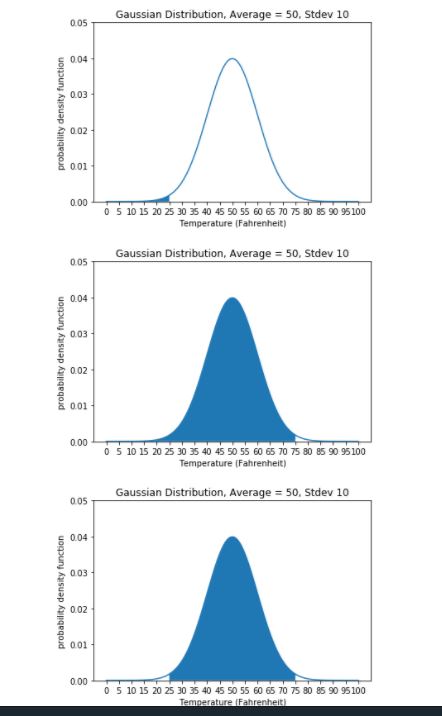
运行下面的代码单元，获取有关如何执行此操作的提示。代码单元输出几个区间的曲线下方面积的可视化，这几个区间分别是从负无穷大到25、从负无穷大到75以及从25到75。

请牢记，cdf方法可以用来计算从负无穷大到你指定数字的曲线下方面积。你如何使用这些信息来计算25 与 75之间的概率？其实，25与75之间的概率等于25与75之间的曲线下方面积。

average = 50
stdev = 10
y_lim = 0.05
x = np.linspace(0, 100, 1000)

plot_fill(x, 0, 25, y_lim,
          'Gaussian Distribution, Average = ' + str(average) + ', Stdev ' + str(stdev))

plot_fill(x, 0, 75, y_lim,
          'Gaussian Distribution, Average = ' + str(average) + ', Stdev ' + str(stdev))

plot_fill(x, 25, 75, y_lim,
          'Gaussian Distribution, Average = ' + str(average) + ', Stdev ' + str(stdev))

在下面填写你的代码。该函数有四个输入和一个输出。下面是输入值：

输入

mean - 高斯分布均值
stdev - 高斯分布标准差
x_low - 概率范围的上限
x_high - 概率范围的下限

输出

x值介于x_low和x_high之间的概率

我们在本课的下一个小节中，即标题为“在Python中计算曲线下方的面积[解决方案]”中，提供了一个解决方案

def gaussian_probability(mean, stdev, x_low, x_high):
    # TODO: return the Gaussian distribution probability
    # that the x-value is between x_low and x_high
    f=norm(loc=mean,scale=stdev).cdf(x_high)-norm(loc=mean,scale=stdev).cdf(x_low)
    
    # Use the SciPy library norm.cdf method
    return f

　运行下面的代码单元格，测试你的结果。本课的下一小节将提供一个解决方案。

assert float('{0:.8f}'.format(gaussian_probability(50, 10, 25, 75))) == 0.98758067
assert float('{0:.2f}'.format(gaussian_probability(50, 10, float('-inf'), float('inf')))) == 1.0
assert float('{0:.8f}'.format(gaussian_probability(50, 10, 20, 60))) == 0.83999485
print('All tests passed')

posted on 2018-04-10 14:47 未完代码阅读(1631) 评论(0) 编辑收藏举报

高斯分布

高斯分布

高斯分布

高斯方程

示例

均值

标准差

曲线下方的面积

高斯概率密度方程下方的面积

曲线下面积

SciPy库

示例：概率密度函数

计算概率

更多示例

练习