1.矩阵的概念
由m×n个数aij排成的m行n列的数表称为矩阵,aij是第i行第j列的元素。
2.特殊矩阵
(1)零矩阵:所有元素aij均为零。
(2)对角矩阵:除对角线上的元素外,其余元素均为零的n阶矩阵。
(3)数量矩阵:主对角线上元素相同的n阶对角矩阵。
(4)单位矩阵:主对角线上的元素均为1的n阶对角矩阵。
(5)三角矩阵:主对角线以下元素均为零n阶对角矩阵称为上三角矩阵,主对角线以上元素均为零的n阶对角矩阵称为下三角矩阵。
3.矩阵的线性运算
(加法、减法、数乘)
矩阵A=(aij)m×n ,矩阵B=(bij)m×n ,
矩阵C=(aij ±bij)m×n
矩阵D=k×A=k×(aij)m×n
A和B必须为同型矩阵
4.性质
(1)交换律:A+B=B+A
(2)结合律:(A+B)+C=A+(B+C) ,(k×l)×A=k×(l×A)
(3)分配律:k×(A+B)=k×A+k×B ,(k+l)×A=kA+kB
5.矩阵乘法
矩阵A和矩阵B相乘必须要满足矩阵A的列数要和矩阵B的行数要相等。
A=(aij)m×n和B=(bij)n×p相乘得到矩阵Cm×p。
(1)结合律:(A×B)C=A(B×C)
(2)分配律:A(B+C)=AB+AC
(3)幂运算(方阵):(Ak)l=Akl
6.矩阵的初等变换
(1)互换矩阵的两行或两列。
(2)用非零数乘以矩阵的某一行或某一列。
(3)用非零数乘以矩阵的某一行后加到另一行的对应元素上。
7.初等矩阵
单位矩阵经过一次初等变换后得到的矩阵。
初等矩阵与初等变换的关系:初等矩阵左乘矩阵A ,相当于对矩阵A做一次相应的初等行变换。初等矩阵右乘矩阵A ,相当于对矩阵A做一次相应的初等列变换。
8.伴随矩阵
设矩阵An×n,由行列式|A|的个元素aij的代数余子式Ai×j所构成的n阶矩阵,记为A*。
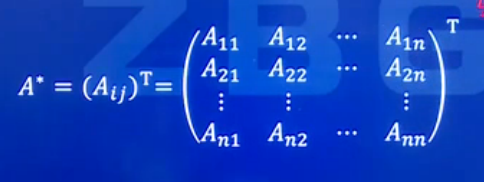
伴随矩阵的性质:
A A=A A*=|A|E
9.逆矩阵
设A 是n阶方阵,若存在方阵B,使得AB=BA=E,则称A是可逆的,矩阵B是A的逆矩阵,记为A-1。
方阵A可逆的充要条件:|A|不等于0,且A-1=(1/|A| )A*
可逆矩阵的性质:
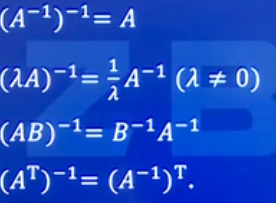
10.矩阵的秩
在m×n的矩阵A中,任取k行k列,位于这些行列交叉处的k2个元素,按照原来的顺序组成一个k阶行列式,称为A的k阶子式,矩阵A的最高阶非零子式的阶数称为矩阵A的秩,记为r(A)。
矩阵秩的公式:




 浙公网安备 33010602011771号
浙公网安备 33010602011771号