力扣 647. 回文子串

647. 回文子串

给你一个字符串 s ，请你统计并返回这个字符串中 回文子串 的数目。

回文字符串 是正着读和倒过来读一样的字符串。

子字符串 是字符串中的由连续字符组成的一个序列。

具有不同开始位置或结束位置的子串，即使是由相同的字符组成，也会被视作不同的子串。

示例 1：

输入：s = "abc"
输出：3
解释：三个回文子串: "a", "b", "c"

示例 2：

输入：s = "aaa"
输出：6
解释：6个回文子串: "a", "a", "a", "aa", "aa", "aaa"

提示：

• 1 <= s.length <= 1000
• s 由小写英文字母组成

题解

来自这里

题目要求统计给定字符串中回文子串的数量。可以使用动态规划来解决该问题。

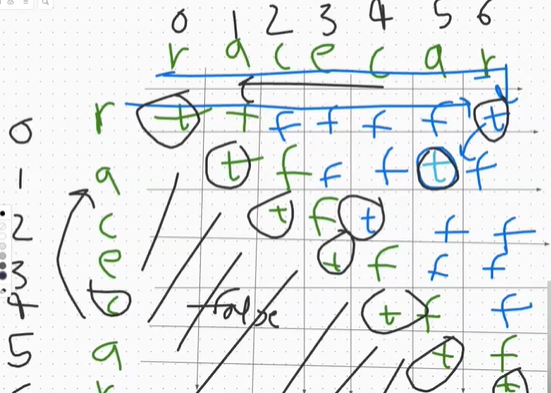
首先，我们定义一个布尔类型的二维数组dp，其中dp[i][j]表示字符串s从索引i到索引j的子串是否是回文串。

然后，我们使用一个变量cnt来记录回文子串的数量，初始化为0。

接下来，我们遍历字符串s中所有可能的子串，从长度为1的子串开始逐渐增加长度。具体的遍历方式是通过两个循环控制，外层循环diff表示子串的长度，内层循环i和j分别表示子串的起始索引和结束索引。

在遍历过程中，我们根据不同的子串长度分情况进行判断：

1. 当子串长度为1时（即diff == 0），子串只有一个字母，必定是回文串，因此将dp[i][j]设置为true。
2. 当子串长度为2时（即diff == 1），子串有两个字母，如果这两个字母相等，则子串是回文串，否则不是回文串，根据判断结果将dp[i][j]设置为相应的布尔值。
3. 当子串长度大于2时，需要判断子串的两个边缘字母和去掉边缘字母后的子串是否是回文串：
   • 如果去掉边缘字母后的子串是回文串（即dp[i+1][j-1]为true），并且子串的边缘字母相等，则子串是回文串，将dp[i][j]设置为true；否则，子串不是回文串，将dp[i][j]设置为false。

在更新dp[i][j]的同时，根据dp[i][j]的值判断子串是否是回文串，如果是，则将cnt加1。

最后，遍历完所有子串后，返回cnt作为结果，即回文子串的数量。

为什么只关注右上部分

在给定的代码中，只判断对角线右上部分的原因是为了避免重复计算和不必要的判断。

考虑一个回文子串，如果我们已经判断了它是回文串，那么它的左下部分（即索引差值大于0的部分）一定不会影响到它是否是回文串。因此，在计算过程中，我们只需要关注右上部分的子串即可。

举个例子来说明：

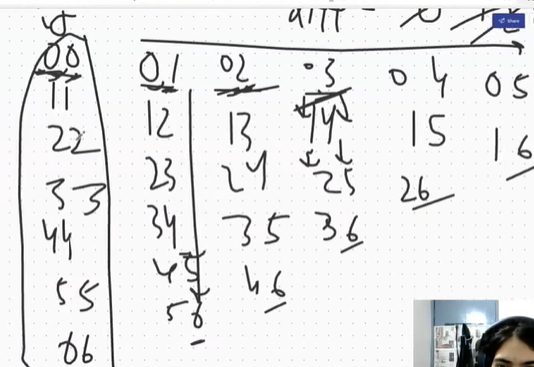
假设字符串s的长度为5，索引从0到4，那么我们需要判断的子串如下所示：

    0 1 2 3 4
0   * * * * *
1     * * * *
2       * * *
3         * *
4           *

对于位置(i, j)，只有右上部分（包括对角线）的子串需要判断是否为回文串，而左下部分的子串已经在之前的迭代中进行过判断。例如，在计算位置(0, 2)时，我们已经计算过(1, 1)，(2, 2)，(3, 3)，(4, 4)这几个位置的子串是否为回文串，因此不需要再重复计算。

通过只判断对角线右上部分的子串，我们可以有效地避免重复计算，减少了时间复杂度。

查看代码

 class Solution {
public:
    int countSubstrings(string s) {
        bool dp[s.length()][s.length()];
        int cnt=0;
        for(int diff=0;diff<s.length();++diff){//子串长度，也是横纵坐标i,j的差值
            for(int i=0,j=diff;j<s.length();++j,++i){//只判断右上部分的，左下部分全为false
                if(diff==0)
                    dp[i][j]=true;//对角线只有一个字母，肯定是true，(00,11,22...)
                else if(diff==1){
                    dp[i][j]=s[i]==s[j]?true:false;//对角线加右边的一个字母，共两个字母，判断，(01,12,23...)
                }else{
                    //结合判断a<bcc>b中的左右边缘字母和里面的<bcc>
                    if(dp[i+1][j-1])//里面的子串是回文,再判断里面的子串
                        dp[i][j]=s[i]==s[j]?true:false;
                    else//里面不是当前串肯定不是
                        dp[i][j]=false;
                }
                // if(dp[i][j])
                //     ++cnt;
                cnt=dp[i][j]?cnt+1:cnt;
            }
        }
        return cnt;
    }
};