力扣 72. 编辑距离

72. 编辑距离

给你两个单词 word1 和 word2， 请返回将 word1 转换成 word2 所使用的最少操作数  。

你可以对一个单词进行如下三种操作：

• 插入一个字符
• 删除一个字符
• 替换一个字符

示例 1：

输入：word1 = "horse", word2 = "ros"
输出：3
解释：
horse -> rorse (将 'h' 替换为 'r')
rorse -> rose (删除 'r')
rose -> ros (删除 'e')

示例 2：

输入：word1 = "intention", word2 = "execution"
输出：5
解释：
intention -> inention (删除 't')
inention -> enention (将 'i' 替换为 'e')
enention -> exention (将 'n' 替换为 'x')
exention -> exection (将 'n' 替换为 'c')
exection -> execution (插入 'u')

提示：

• 0 <= word1.length, word2.length <= 500
• word1 和 word2 由小写英文字母组成

题解

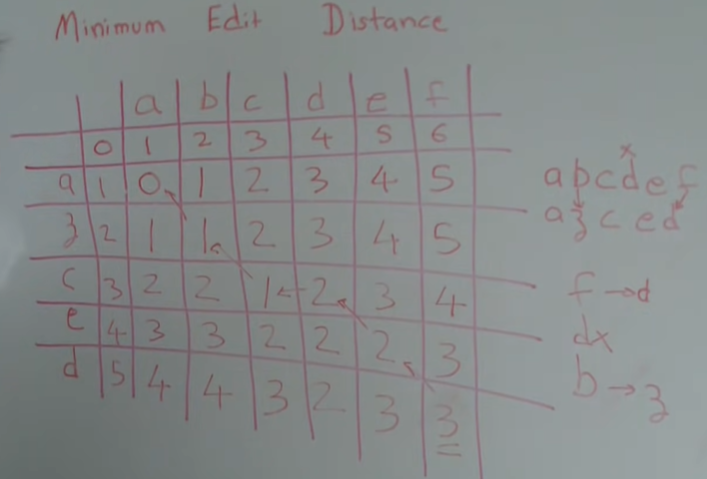
思路如下：

1. 创建一个二维数组 dp，大小为 (word2.length()+1) × (word1.length()+1)，其中 dp[i][j] 表示将 word1 的前 j 个字符转换为 word2 的前 i 个字符所需的最小操作数。
2. 初始化第一行和第一列的值：
   • dp[0][j] 表示将空字符串转换为 word1 的前 j 个字符，需要进行的操作数为 j。
   • dp[i][0] 表示将 word2 的前 i 个字符转换为空字符串，需要进行的操作数为 i。
3. 对于 dp[i][j]，根据当前字符进行判断：
   • 如果 word1[j-1] 和 word2[i-1] 相等，即当前字符相同，那么不需要进行任何操作，dp[i][j] = dp[i-1][j-1]。
   • 如果 word1[j-1] 和 word2[i-1] 不相等，即当前字符不同，那么需要进行操作，包括插入、删除和替换操作。根据题目要求，取这三种操作中的最小值加上一次操作，即 dp[i][j] = min(dp[i-1][j-1], dp[i][j-1], dp[i-1][j]) + 1。
4. 遍历完成后，dp[word2.length()][word1.length()] 即为将 word1 转换为 word2 所需的最小操作数。

来自：https://www.youtube.com/watch?v=We3YDTzNXEk

查看代码

 class Solution {
public:
    int minDistance(string word1, string word2) {
        int dp[word2.length()+1][word1.length()+1];
        for(int i=0;i<=word2.length();++i)
            dp[i][0]=i;
        for(int i=0;i<=word1.length();++i)
            dp[0][i]=i;
        for(int i=1;i<=word2.length();++i){
            for(int j=1;j<=word1.length();++j){
                if(word1[j-1]==word2[i-1])
				    dp[i][j] = dp[i - 1][j - 1];
			    else
				    dp[i][j]=min(dp[i-1][j-1],min(dp[i][j-1],dp[i-1][j]))+1;
            }
        }
        return dp[word2.length()][word1.length()];
    }
};