力扣 968. 监控二叉树

968. 监控二叉树

给定一个二叉树，我们在树的节点上安装摄像头。

节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。

计算监控树的所有节点所需的最小摄像头数量。

示例 1：

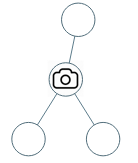
输入：[0,0,null,0,0]
输出：1
解释：如图所示，一台摄像头足以监控所有节点。

示例 2：

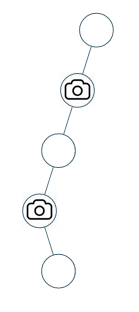
输入：[0,0,null,0,null,0,null,null,0]
输出：2
解释：需要至少两个摄像头来监视树的所有节点。 上图显示了摄像头放置的有效位置之一。

提示：

1. 给定树的节点数的范围是 [1, 1000]。
2. 每个节点的值都是 0。

题解

来自：https://www.youtube.com/watch?v=fORHMo5yzNk

因为节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。优先不会给叶子节点加摄像头，优先加在父节点上，即节点是否加摄像头，要判断其和子节点的情况。因此遍历方向从下往上，采用递归。

父节点a和子节点a,b，abc的状态初始都是需要被监控的，记为want，摄像头加在a上，可以同时实现三个的监控，记装备监控的节点状态为provide，则子节点都被包含了，即b,c状态为ok,即被监控且非装备摄像头的状态，考虑以下几种情况：

• 如果在树中，b状态为ok，c为want，那么a也需要装备摄像头，否则c不会被监控=>有一个子树状态为want，则父需要装备摄像头，置状态为provide；
• 如果在树中，b,c状态为ok，那么a的状态为初始状态want；
• 如果在树中，b/c状态为provide，则a状态为ok；

伪代码如下：

if one child "want":parent "provide"
 else if one child "provide": parent "ok"
 else: parent "want"

在编码中可以用int表示状态来替代string：ok-0 want-1 provide-2

查看代码

 /**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int numCamera=0;
    //ok-0 want-1 provide-2
    int work(TreeNode* cur){
        if(cur==NULL)//空节点不需要
            return 0;
        int left=work(cur->left);//递归寻找左子树状态
        int right=work(cur->right);//递归寻找右子树状态
        //只要有一个子树需要，父节点就需要提供
        if(left==1||right==1){
            ++numCamera;
            return 2;
        }
        //只要有一个子树提供了，父节点就被监控了
        else if(left==2||right==2){
            return 0;
        }
        return 1;//叶子节点需要监控
    }
    int minCameraCover(TreeNode* root) {
        if(work(root)==1)//考虑只有一个节点
            ++numCamera;
        return numCamera;
    }
};