堆介绍与实现

堆介绍

实现可以通过跳表、二叉堆。

详细介绍来自Heap Tree

最小堆积(Min heap):父节点小于等于子节点

最大堆积(Max heap):父节点大于等于子节点（但是下一层的节点不一定比上一层的所有节点都小）

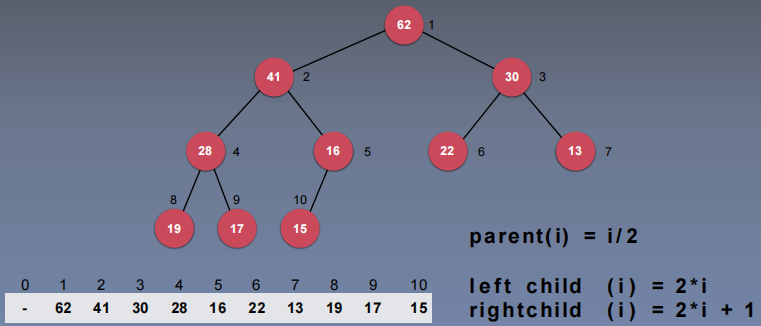
基于数组实现二叉堆

二叉堆是一棵完全二叉树，当前节点下标i和其父、子节点之间的关系为：

parent(i) = i/2

l e f t child ( i ) = 2 * i

rightchild ( i ) = 2 * i + 1

向堆中添加元素和ShiftUp

添加52，先添加在数组最尾端，然后选取倒数第二层的节点（即叶子节点的父节点），一步步shiftUp（从数组下标4开始，直到顶节点0），直到满足最大堆的性质，即父节点大于两个子节点。

shiftUp：当前子树父节点a，左右节点b,c，选取b,c中最大的节点m与a进行比较，如果m>a，交换m与a

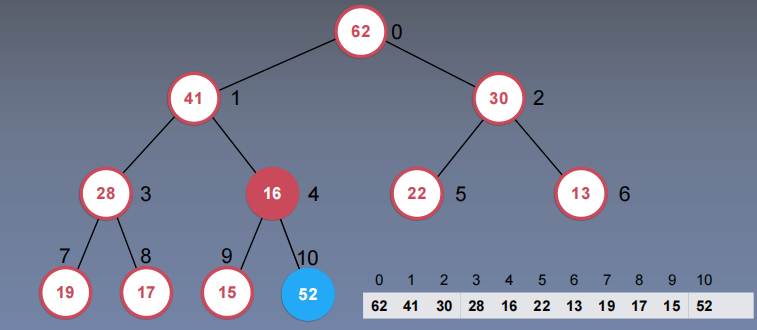
1.交换52和16，

2.交换41和52，满足性质不再交换，得到如下

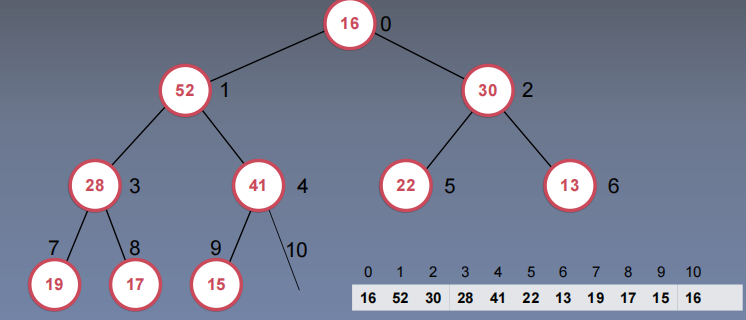
取出堆中的最大元素和Shift Down

1.先删除最尾端节点16

2.将16赋值给顶端节点62，那么此时不再满足大顶堆性质

3.将62依次shiftDown，直到满足性质

shiftDown：操作同shiftUp,只是返回的下标不一样

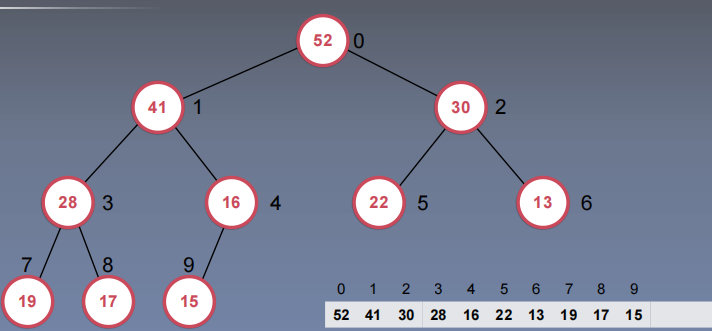
replace

replace：取出最大元素后，放入一个新元素

实现：可以先extractMax，再add，两次O(logn)的操作

更优的实现：可以直接将堆顶元素替换以后Shift Down，一次O(logn)的操作

heapify

heapify：将任意数组整理成堆的形状

实现

实现：先将数组原arr直接放入二叉堆的数组，然后从数组最尾端开始往前shiftDown

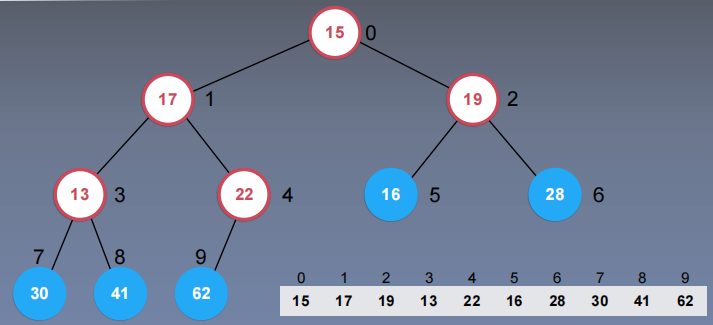
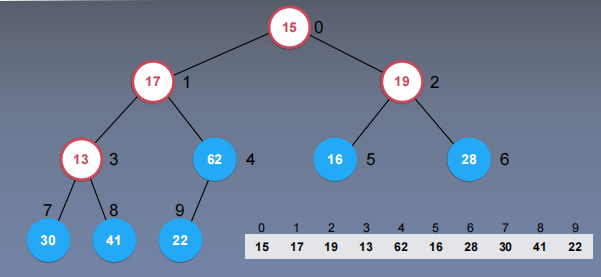
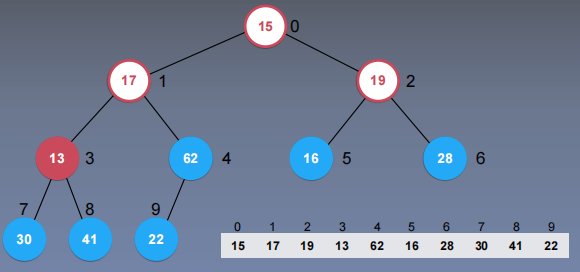
接下来15继续shiftDown

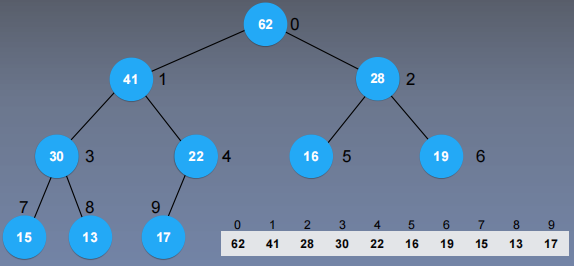
Heapify 的算法复杂度

将n个元素逐个插入到一个空堆中，算法复杂度是O(nlogn)

heapify的过程，算法复杂度为O(n)

优先队列

在c中可以通过优先队列实现堆结构

介绍

来自优先队列(priority_queue)的原理及用法

std::priority_queue:在优先队列中，优先级高的元素先出队列，并非按照先进先出的要求，类似一个堆(heap)。其模板声明带有三个参数，priority_queue<Type, Container, Functional>, 其中Type为数据类型，Container为保存数据的容器，Functional为元素比较方式。Container必须是用数组实现的容器，比如 vector, deque. STL里面默认用的是vector. 比较方式默认用operator< , 所以如果把后面两个参数缺省的话，优先队列就是大顶堆，队头元素最大。

默认大顶堆，通过 greater<>声明小顶堆，如：priority_queue<int,vector<int> , greater<>> pq;

基本操作：

优先队列在头文件#include <queue>中；

其声明格式为：priority_queue <int> ans;//声明一个名为ans的整形的优先队列

empty( )  //判断一个队列是否为空

pop( )  //删除队顶元素

push( )  //加入一个元素

size( )  //返回优先队列中拥有的元素个数

top( )  //返回优先队列的队顶元素

优先队列的时间复杂度为O（logn），n为队列中元素的个数，其存取都需要时间。

使用示例：

查看代码

#include <bits/stdc++.h>
using namespace std;
 
int main()
{
	vector<int> aa = { 1,2,4,3,8,6,1,4 };
	priority_queue<int, greater<>> pq;//, vector<int>
	for (int i = 0; i < aa.size(); i++) {
		pq.push(aa[i]);
	}
	sort(aa.begin(), aa.end());
	for (int i = 0; i < aa.size(); i++)
		cout << aa[i] << endl;
	for (int i = 0; i < aa.size(); i++){
		cout << pq.top() << endl;
	pq.pop();
}
	//cout << pq << endl;
	system("pause");
	return 0;
}