力扣 110. 平衡二叉树 [基础+优化]

110. 平衡二叉树

给定一个二叉树，判断它是否是高度平衡的二叉树。

本题中，一棵高度平衡二叉树定义为：

一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。

 

示例 1：

输入：root = [3,9,20,null,null,15,7]
输出：true

示例 2：

输入：root = [1,2,2,3,3,null,null,4,4]
输出：false

示例 3：

输入：root = []
输出：true

提示：

• 树中的节点数在范围 [0, 5000] 内
• -104 <= Node.val <= 104

基础思路

题目要求每个节点 的左右两个子树的高度差的绝对值不超过 1，则每棵子数都要满足高度差的条件，构造一个函数getD(cur)，计算以cur为根节点的树的最大高度，使用递归依次计算每棵树是否平衡，所有都满足则返回true，否则false。

构造函数getD(cur)：

getDepth伪代码

 int getDepth(TreeNode* cur){
        if(!cur)//当前节点为空
            return 0;
        if cur没有左子树 || cur没有右子树//只有cur这一个节点，则以cur为根节点的树高度为1
            return 1;
        if cur左右子树都存在//返回子数中最高的高度＋1（1是cur这一层占一个高度）    
            return 1+max(getDepth(cur->left),getDepth(cur->right));
    }

优化

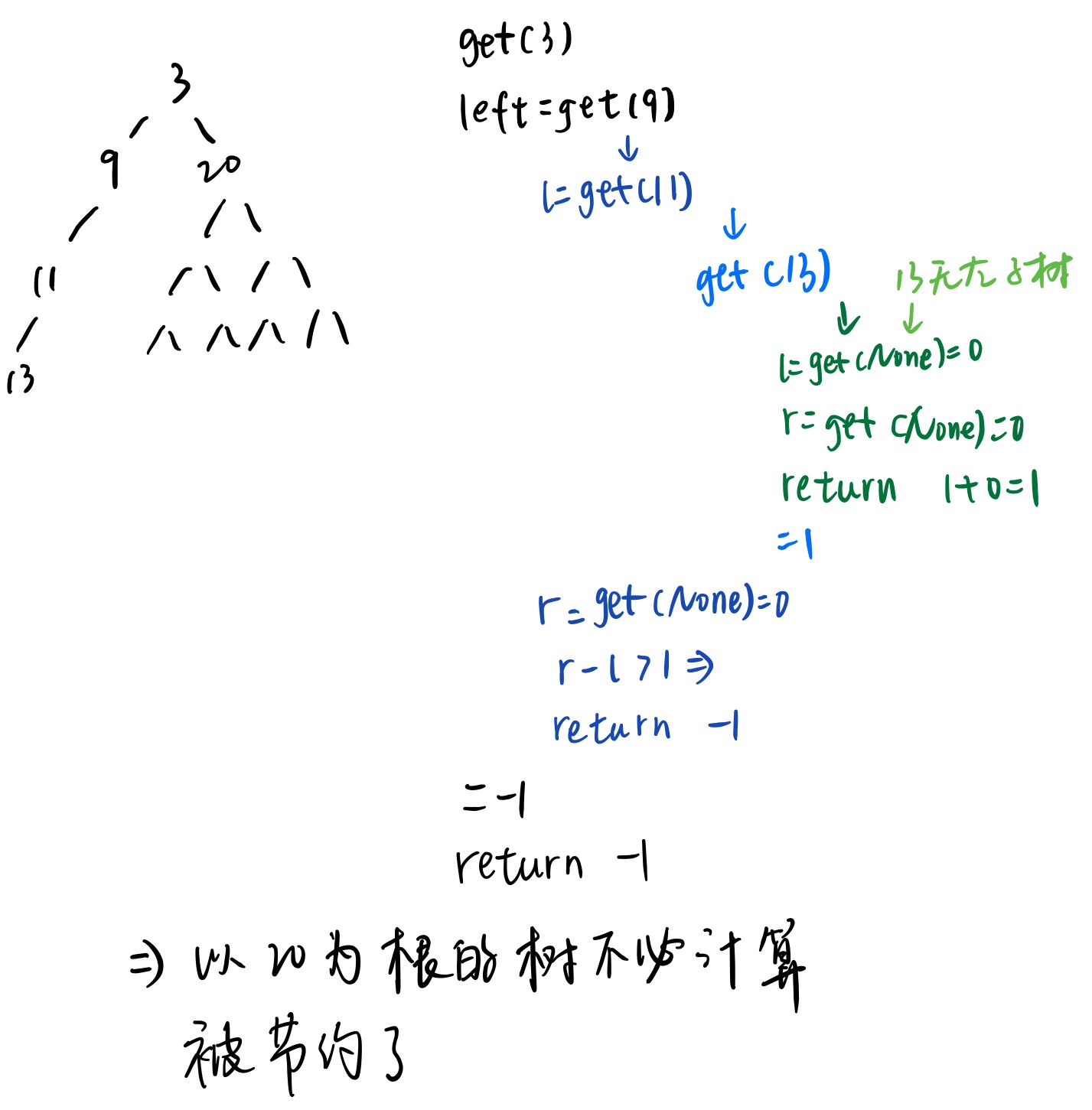
如果使用基础思路，会出现很多重复无用的计算，题目比如cur的左子树高度计算得到left已经不平衡，则无需计算右子树right的高度去比较是否平衡，也无需计算cur的高度。

因此优化在递归计算高度时，同时计算出是否满足平衡条件，left不仅表示左子树的高度，还增加-1的值表示左子树是否平衡，如果不平衡则节约right的计算和是否平衡的计算，直接将cur高度返回为-1，right==-1同理，如果左右子数都平衡，则计算cur这棵树的高度进行返回。

例子如下图：

优化代码

 /**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int getDepth(TreeNode* cur){
        if(!cur)//当前节点为空，则高度0
            return 0;
        int left=getDepth(cur->left);//获取左子数的高度
        if(left==-1)//左子树不平衡，则直接返回-1，表示cur这棵树不平衡
            return -1;
        int right=getDepth(cur->right);//获取右
        if(right==-1)//表示cur这棵树不平衡
            return -1;
        if(abs(left-right)>1)//计算cur这棵树是否平衡
            return -1;
        else
            return 1+max(left,right);//平衡，则返回cur这棵树的高度
    }
    bool isBalanced(TreeNode* root) {
        if(getDepth(root)==-1)
            return false;
        else
            return true;
    }
};