二叉树基础

遍历顺序

深度优先遍历

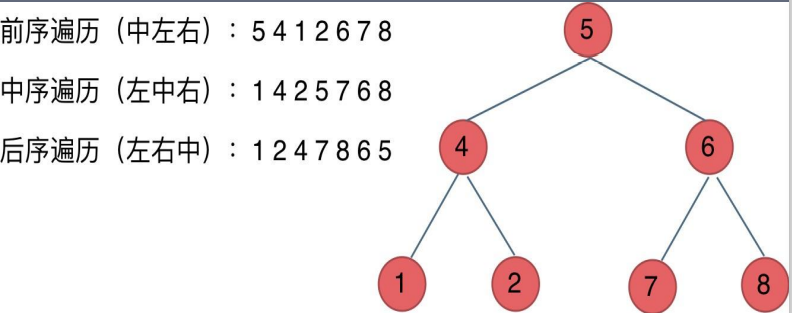
前序遍历：中左右

中序遍历：左中右

后序遍历：左右中

广度优先遍历（层序遍历）

从上到下，从左到右：5 4 6 1 2 7 8 

例题+代码（建树和遍历）

UVA 536:建树和输出

题意：

给出先序和中序，求后序。

Sample Input
DBACEGF ABCDEFG
BCAD CBAD
Sample Output
ACBFGED
CDAB

#include<iostream>
#include<cstdio>
#include<queue>
#include<cstring>
using namespace std;

int n;
char pre[1010],mid[1010];
int judge[1010];
//二叉树结构体
struct node{
	char c;//存放此节点的值
	node *left,*right;
	node()
	{
		c='a';
		left=right=NULL;
	}
};
int cnt=0,counter;
//建树
node* build(node *root)
{
	char c=pre[cnt++];//从pre中取数 去mid中查找
       int i;
       for( i=0;i<n;i++)
       {
           if(mid[i]==c)
           break;
       }
       judge[i]=1;
       root=new node();
       root->c=c;
       if(i>0&&i<n&&judge[i-1]!=1)//在mid数组中，如果一个数左相邻的数被标记，则不能向左建树
           root->left=build(root->left);
       if(i>=0&&i<n-1&&judge[i+1]!=1)//同样，在mid数组中，如果一个数右相邻的数被标记，则不能向右建树
           root->right=build(root->right);
       return root;    //左右都建完，返回根结点
}
//后序输出（左右中）：递归，先左，后右，再中
void postorder(node *root)
{
	if(root->left)
	postorder(root->left);
	if(root->right)
	postorder(root->right);
	printf("%c",root->c);
}

int main()
{
	while(scanf("%s %s",pre,mid)==2)//输入先序和后序遍历
	{
		counter = 0;
		cnt = 0;
		n=strlen(pre);
		memset(judge,0,sizeof(judge));
		
		node *root = NULL;
        //建树
		root = build(root);
        //后序输出
		postorder(root);
		printf("\n");
	}
	return 0;
}

 还有可以不建树的方法

PTA L2-011 

题意：

给定一棵二叉树的中序遍历和前序遍历，请你先将树做个镜面反转，再输出反转后的层序遍历的序列。所谓镜面反转，是指将所有非叶结点的左右孩子对换。这里假设键值都是互不相等的正整数。

输入格式：

输入第一行给出一个正整数N（$\le$30），是二叉树中结点的个数。第二行给出其中序遍历序列。第三行给出其前序遍历序列。数字间以空格分隔。

输出格式：

在一行中输出该树反转后的层序遍历的序列。数字间以1个空格分隔，行首尾不得有多余空格。

输入样例：

7
1 2 3 4 5 6 7
4 1 3 2 6 5 7

输出样例：

4 6 1 7 5 3 2

思路：

先建树，然后按层次输出。

#include<iostream>
#include<cstring>
#include<cstdio>
#include<cstdlib>
#include<sstream>
#include<list>
#include<cmath>
#include<queue>
using namespace std;
struct node{
    int index;
    node *left,*right;
    node()
    {
        index=0;
        left=right=NULL;
    }
};
int pre[33],mid[33];
int n2,n;
int judge[300];
node* build(node *root)//建树
{
    int t=pre[n2++];
    int i;

    for( i=0;i<n;i++)
    {
        if(mid[i]==t)
        break;
    }
    root=new node();
    root->index=t;
    judge[i]=1;
    if(i>0&&i<n&&judge[i-1]==0)
    root->left=build(root->left);
    if(i>=0&&i<n-1&&judge[i+1]==0)
    root->right=build(root->right);
    return root;
}

void print(node* root)
{
    printf("%d ",root->index);
    if(root->left)
    print(root->left);
    if(root->right)
    print(root->right);
    return ;
}
int cntp=0;
void bfs(node* root)//题目要求层次遍历输出
{
    queue <node*> q;
    q.push(root);
    while(!q.empty())
    {
        node* a=q.front();
        q.pop();
        if(cntp!=0)
        printf(" ");
        printf("%d",a->index);
        cntp++;
        if(a->right)//翻转，先右后左
        q.push(a->right);
        if(a->left)
        q.push(a->left);

    }
    return ;
}
int main()
{

    while(scanf("%d",&n)==1)
    {
        for(int i=0;i<n;i++)
        scanf("%d",&mid[i]);
        for(int i=0;i<n;i++)
        scanf("%d",&pre[i]);
        memset(judge,0,sizeof(judge));
        n2=0;
        cntp=0;
        node* root=build(root);
        //print(root);
        bfs(root);
        printf("\n");
    }
    return 0;
}

中序遍历

中序遍历按照左 -> 中 -> 右的顺序，通过中序遍历二叉搜索树得到的遍历结果需要满足升序条件。

查看代码

 /**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool isValidBST(TreeNode* root) {
        // if(root==nullptr)
        //     return true;
        stack<TreeNode*> sta;
        long long lastValue=LONG_MIN;// (long long)INT_MIN - 1;
        while(!sta.empty()||root!=nullptr){
            while(root!=nullptr){//中序遍历（左-中-右）：依次放入左节点,stack先进后出，会依次push出叶子左节点(左)和非叶子左节点根节点（中）
                sta.push(root);
                root=root->left;
            }
            root=sta.top();//
            sta.pop();
            if(root->val<=lastValue)//不满足升序，无效
                return false;
            lastValue=root->val;//更新
            root=root->right;//可能为Null，切换到右
        }
        return true;
    }
};