力扣 42. 接雨水 自己+官方双指针

42. 接雨水

难度困难

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

示例 1：

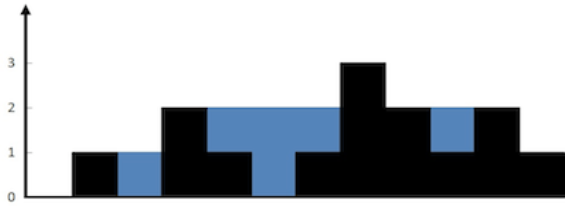
输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出：6
解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。 

示例 2：

输入：height = [4,2,0,3,2,5]
输出：9

提示：

• n == height.length
• 1 <= n <= 2 * 104
• 0 <= height[i] <= 105

 自己：爬楼梯

以示例一为例，height = [0,1,0,2,1,0,1,3,2,1,2,1]前半部分像爬楼梯一样，最高的点在逐步升高（高度为1，2，3），我们先计算这种前半部分这种升高的情况：

用l来记录当前最高柱子的下标，往右移动：

• 当前柱子高度h<当前最高柱子，用t把h记录并累计起来，
• 当前柱子高度h>当前最高柱子，如下图
  • 计算红色边框长方形面积：长为两根高柱子中较短的一根，宽为两个柱子之间的距离
  • 减去长方形里面的黑色矩形，也就是减去两个高柱子之间的柱子，注意我们用t表示的两个高柱子之间的所有柱子的高度，t=长方形中两个黑色矩形的面积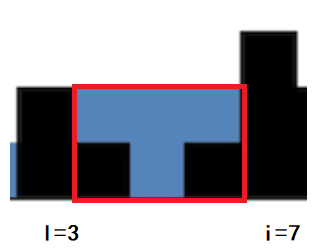
  • 
  • 更新t和l:l变成当前最高的柱子i,t复位
• 这样出现的问题是：如果全场最高的柱子不在最右端，那么此柱子后面都不会计算，所以：
  • 在移动到最右端后，我们判断最高柱子是否在此处，不在就从右往左，最右端=>全场最高柱子，倒过来再算

查看代码

class Solution {
public:
    int trap(vector<int>& height) {
        int res=0;
        int n=height.size();
        int l=0;
        int t=0;
        while(l<n&&height[l]==0){//找到起始点
            l++;
        }
        for(int i=l+1;i<n;i++){
            if(height[l]>height[i])//继续走
            {
                t+=height[i];//记录当前高度，可能是0，1，2xxx
            }
            else if(height[l]<=height[i]){
                res+=(i-l-1)*(min(height[l],height[i]))-t;//res加上每次的量（长*宽-原有的高度）
                l=i;//更新l
                t=0;//复位
            }

        }
        if(l<n){//如果没有到最后，说明最大值在中间，从右往左再算一次
            t=0;
            int r=n-1;
            while(height[r]==0){
                r--;
            }
            for(int i=r-1;i>=l;i--){
                if(height[r]>height[i])//继续走
                {
                    t+=height[i];//记录当前高度，可能是0，1，2xxx
                }
                else if(height[r]<=height[i]){
                    res+=(r-i-1)*(min(height[r],height[i]))-t;
                    r=i;
                    t=0;
                }
            }
        }
        return res;
    }
};

官方：双指针

链接

如果可以看了一个方法，那么更容易理解这个。上一个方法是寻找两个较高的柱子，看成一个长方形面积减去几个矩形的求解，

这个方法是从两端开始遍历往中间靠，两个指针 left 和 right，以及两个变量 leftMax 和 rightMax，

那么两端互为自己的底线，即不管中间有没有柱子，有多少柱子，这两端都可以保底，看作两端之间都没有其他柱子，每次计算一端可以接水的量，只要此时

• height[left]<height[right]，则必有leftMax<rightMax，下标left 处能接的雨水量等于leftMax−height[left]，将下标 left 处能接的雨水量加到能接的雨水总量，然后将left 加 1（即向右移动一位）；
• height[left]≥height[right]，则必有 leftMax≥rightMax，下标 right 处能接的雨水量等于 rightMax−height[right]，将下标 right 处能接的雨水量加到能接的雨水总量，然后将 right 减 1（即向左移动一位）。

当两个指针相遇时，即可得到能接的雨水总量。

查看代码

class Solution {
public:
    int trap(vector<int>& height) {
        int res=0;
        int right=height.size()-1;
        int left=0;
        int maxl=0,maxr=0;
        while(left<=right){
            if(height[left]>maxl)
                maxl=height[left];
            if(height[left]<height[right]){
                res+=maxl-height[left];
                left++;
            }
            if(height[right]>maxr)
                maxr=height[right];
            if(height[left]>=height[right]){
                res+=maxr-height[right];
                right--;
            }
        }
        return res;
    }
};