力扣 40. 组合总和 II (dfs+有意思)

40. 组合总和 II

给定一个候选人编号的集合 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的每个数字在每个组合中只能使用 一次 。

注意：解集不能包含重复的组合。 

示例 1:

输入: candidates = [10,1,2,7,6,1,5], target = 8, 输出: [ [1,1,6], [1,2,5], [1,7], [2,6] ]

示例 2:

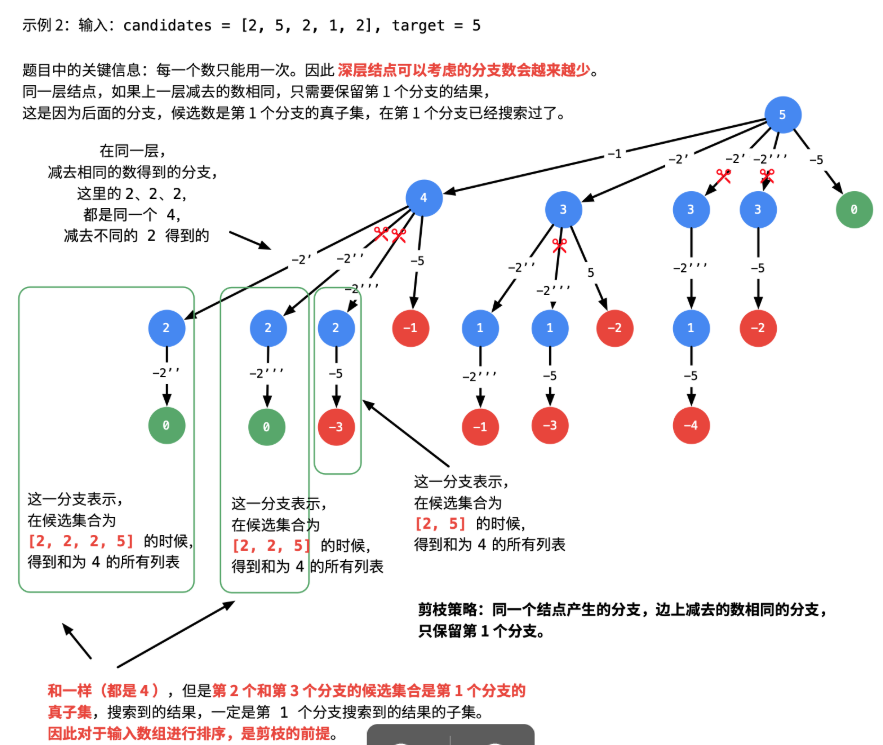
输入: candidates = [2,5,2,1,2], target = 5,
输出:
[
[1,2,2],
[5]
]

提示:

• 1 <= candidates.length <= 100
• 1 <= candidates[i] <= 50
• 1 <= target <= 30

官方题解

链接

在求出组合的过程中就进行去重的操作。我们可以考虑将相同的数放在一起进行处理，也就是说，如果数 x 出现了 y次，那么在递归时一次性地处理它们，即分别调用选择 0, 1, ..., y次 x 的递归函数。这样我们就不会得到重复的组合。具体地：

我们使用一个哈希映射（HashMap）统计数组 candidates 中每个数出现的次数。在统计完成之后，我们将结果放入一个列表 freq 中，方便后续的递归使用。

列表 freq 的长度即为数组candidates 中不同数的个数。其中的每一项对应着哈希映射中的一个键值对，即某个数以及它出现的次数。
在递归时，对于当前的第pos 个数，它的值为 freq[pos][0]，出现的次数为 freq[pos][1]，那么我们可以调用

dfs(pos+1,rest−i×freq[pos][0])

即我们选择了这个数 i 次。这里 i不能大于这个数出现的次数，并且 i×freq[pos][0] 也不能大于 rest。同时，我们需要将 i 个 freq[pos][0] 放入列表中。

这样一来，我们就可以不重复地枚举所有的组合了。

我们还可以进行什么优化（剪枝）呢？一种比较常用的优化方法是，我们将 freq 根据数从小到大排序，这样我们在递归时会先选择小的数，再选择大的数。这样做的好处是，当我们递归到 dfs(pos,rest) 时，如果freq[pos][0] 已经大于rest，那么后面还没有递归到的数也都大于 rest，这就说明不可能再选择若干个和为 rest 的数放入列表了。此时，我们就可以直接回溯。

查看代码

class Solution {
private:
    vector<pair<int, int>> freq;
    vector<vector<int>> ans;
    vector<int> sequence;

public:
    void dfs(int pos, int rest) {
        if (rest == 0) {//找到符合条件的组合
            ans.push_back(sequence);
            return;
        }
        if (pos == freq.size() || rest < freq[pos].first) {//剪枝：遍历完或者剩下的数都比rest大
            return;
        }

        dfs(pos + 1, rest);//跳过当前

        int most = min(rest / freq[pos].first, freq[pos].second);//次数不能大于最多出现次数
        for (int i = 1; i <= most; ++i) {//枚举次数
            sequence.push_back(freq[pos].first);
            dfs(pos + 1, rest - i * freq[pos].first);//选取当前
        }
        for (int i = 1; i <= most; ++i) {
            sequence.pop_back();
        }
    }

    vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
        sort(candidates.begin(), candidates.end());
        for (int num: candidates) {
            if (freq.empty() || num != freq.back().first) {
                freq.emplace_back(num, 1);//放入freq
            } else {
                ++freq.back().second;//已经放入了就++
            }
        }
        dfs(0, target);
        return ans;
    }
};

大神题解

链接

总的想法：先排序，在同一层的时候判断是不是与前一个数相同，如果相同就跳过

如何去掉重复的集合（重点）
为了使得解集不包含重复的组合。有以下 22 种方案：

• 使用 哈希表 天然的去重功能，但是编码相对复杂；
• 这里我们使用和第 39 题和第 15 题（三数之和）类似的思路：不重复就需要按 顺序 搜索， 在搜索的过程中检测分支是否会出现重复结果 。注意：这里的顺序不仅仅指数组 candidates 有序，还指按照一定顺序搜索结果。

由第 39 题我们知道，数组 candidates 有序，也是 深度优先遍历 过程中实现「剪枝」的前提。
将数组先排序的思路来自于这个问题：去掉一个数组中重复的元素。很容易想到的方案是：先对数组 升序 排序，重复的元素一定不是排好序以后相同的连续数组区域的第 1个元素。也就是说，剪枝发生在：同一层数值相同的结点第 2、3 ... 个结点，因为数值相同的第 1 个结点已经搜索出了包含了这个数值的全部结果，同一层的其它结点，候选数的个数更少，搜索出的结果一定不会比第 1 个结点更多，并且是第 1 个结点的子集。

// author:rmokerone
#include <iostream>
#include <vector>

using namespace std;

class Solution {

private:
    vector<int> candidates;
    vector<vector<int>> res;
    vector<int> path;
public:
    void DFS(int start, int target) {
        if (target == 0) {
            res.push_back(path);
            return;
        }

        for (int i = start; i < candidates.size() && target - candidates[i] >= 0; i++) {
            if (i > start && candidates[i] == candidates[i - 1])
                continue;
            path.push_back(candidates[i]);
            // 元素不可重复利用，使用下一个即i+1
            DFS(i + 1, target - candidates[i]);
            path.pop_back();
        }
    }

    vector<vector<int>> combinationSum2(vector<int> &candidates, int target) {
        sort(candidates.begin(), candidates.end());//排序是判断重复的基础
        this->candidates = candidates;
        DFS(0, target);
        return res;
    }
};