51Nod 1022 石子归并 V2（区间DP+四边形优化）

题目链接：http://www.51nod.com/onlineJudge/questionCode.html#!problemId=1022

题目大意：

N堆石子摆成一个环。现要将石子有次序地合并成一堆。规定每次只能选相邻的2堆石子合并成新的一堆，并将新的一堆石子数记为该次合并的代价。计算将N堆石子合并成一堆的最小代价。

例如： 1 2 3 4，有不少合并方法

1 2 3 4 => 3 3 4(3) => 6 4(9) => 10(19)

1 2 3 4 => 1 5 4(5) => 1 9(14) => 10(24)

1 2 3 4 => 1 2 7(7) => 3 7(10) => 10(20)

括号里面为总代价可以看出，第一种方法的代价最低，现在给出n堆石子的数量，计算最小合并代价。

 解题思路：经典的石子合并问题，较原来不同的是石子是环形摆放的，而且石子数目n的范围有100增加到了1000，原本O（n^3）的算法肯定是会超时的。所以需要用四边形不等式优化将复杂度降为O（n^2），并且将数组倍增把环变为链。

粗略介绍一下四边形优化的作用，具体证明看这里《动态规划加速原理之四边形不等式》。

我们原本的状态转移方程为dp[i][j]=min{dp[i][k]+dp[k+1][j]+w[i][j]}（i<j，i<=k<=j）。

上式在动态规划的状态转移方程中是很常见的，对于上式中的w(i,j)
如果符合w(i`,j) <= w(i,j`) i<i`<j<j`        那么我们称函数w满足关于区间包含的单调性。
如果符合w(i,j)+w(i`,j`) <= w(i`,j)+w(i,j`)    那么我们称函数w满足四边形不等式。

那么就可以使用两个定理（图片来源）

于是，我们可以使用s[i][j]记录使得dp[i][j]最优的分割点（k点），并且满足s[i][j-1]<=s[i][j]<=s[i+1][j+1]，那么我们的k的枚举范围就是s[i][j-1]<=s[i][j]<=s[i+1][j+1]。

复杂度证明:

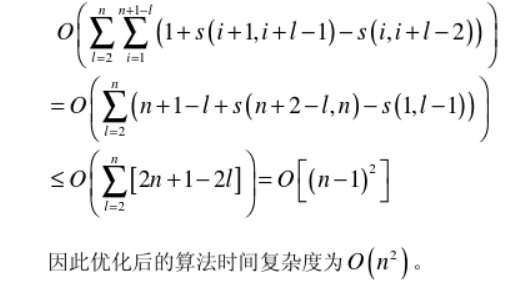
代码：

#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
using namespace std;
const int N=2e3+5;
const int INF=0x3f3f3f3f;

int dp[N][N],s[N][N],sum[N],a[N];//s[i][j]为使dp[i][j]最优的分割点 

int main(){
    int n;
    scanf("%d",&n);
    memset(dp,0x3f,sizeof(dp));
    for(int i=1;i<=n;i++){
        scanf("%d",&a[i]);
        a[i+n]=a[i];
    }
    for(int i=1;i<=2*n;i++){
        dp[i][i]=0;
        sum[i]=sum[i-1]+a[i];
        s[i][i]=i;
    }
    for(int d=1;d<n;d++){
        for(int i=1;i<=2*n-d;i++){
            int j=i+d;
            for(int k=s[i][j-1];k<=s[i+1][j];k++){
                int tmp=dp[i][k]+dp[k+1][j]+sum[j]-sum[i-1];
                if(tmp<dp[i][j]){
                    dp[i][j]=tmp;
                    s[i][j]=k;
                }
            }
        }
    }
    int ans=INF,d=n-1;
    for(int i=1;i<=2*n-d;i++){
        int j=i+d;
        ans=min(ans,dp[i][j]);
    }
    printf("%d\n",ans);
    return 0;
}