python学习日记——利用python进行数据分析

一、基础

1.python中的各种推导式（列表推导式、字典推导式、集合推导式）

列表推导式：
    datalist = [i**2 for i in range(30) if i % 3 is 0]
字典推导式：
    from numpy.random import randn
    datadict = {i:randn() for i in range(7)}
集合推导式：
    dataset = {x**2 for x in [1, 1, 2]}

2.matplotlib

import matplotlib.pyplot as plt
img = plt.imread("C:\\Users\\Administrator\\Pictures\\1.jpg")
plt.imshow(img)
plt.show()

注意：plt.imshow()函数负责对图像进行处理并显示其格式；plt.show()函数则是将plt.imshow()处理过后的图像显示出来

二、numpy基础

 1.ndarray对象

# 创建ndarray对象，以下是创建从一维到高维的数组
data1 = np.array(1.4)
data2 = np.array([1.5,1.6,1.7])
data3 = np.array([[1.25,3.14],[1.41,2.71]])
data4 = np.array([[[1.25,3.14],[1.41,2.71]],[[1.25,3.14],[1.41,2.71]]])

print(np.zeros((3,4))) #创建值全为0的数组（矩阵），维度是传入的元组
print(np.ones((3,4))) #创建值全为1的数组（矩阵），维度是传入的元组
print(np.eye(4)) #创建对应行列式的值为1的数组（矩阵），行列数对应传入整数
print(np.empty((3,4))) #创建值随机的数组（矩阵），维度是传入的元组

# ndarray对象的取值
print(data3[0][0])
print(data4[0][0][1])
print(data4[0,0,1])

# ndarray对象的内置方法
print(data3.transpose()) #打印矩阵3的转置矩阵
print(data4.shape) #打印数组的维度
print(data4.dtype) #打印数组中值的类型
print(data4[0].copy()) #显式复制

# ndarray支持切片索引

 numpy.random中的randn()函数——生成正态分布的随机数据，参数是生成的数据的维度

data5 = np.random.randn(10,10)
print(data5[:,[6,7,8]]) #第一个:代表行全部选中，第二个[6,7,8]代表选中6,7,8列

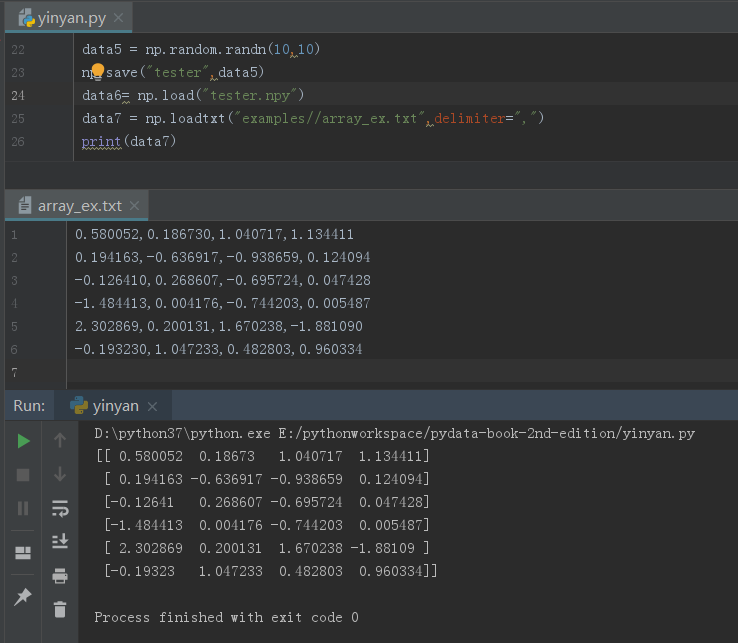
 numpy.save()函数与numpy.load()函数

data5 = np.random.randn(10,10)
np.save("tester.npy",data5) #将数组保存为二进制文件，如果结尾没有.npy会自动加上
data6= np.load("tester.npy") #加载保存数组的二进制文件，并返回ndarray对象
print(data6)

2.线性代数相关

data8 = np.random.randn(2,2)
data9 = np.random.randn(2,2)
y = np.random.randn(2,1)
# 矩阵乘法
print(np.linalg.multi_dot([data8,data9]))
# 矩阵的范数
print(np.linalg.norm(data8))
# 方阵的逆
print(np.linalg.inv(data8))
# 解线性方程组solve(a, b)，`ax = b`.
print(np.linalg.solve(data8,y))
# 线性问题的最小二乘解
data10 = np.random.randn(2,3)
print(np.linalg.lstsq(data10,y,rcond=None))
# 矩阵的伪逆
print(np.linalg.pinv(data10))


源码解释如下：
norm            Vector or matrix norm
inv             Inverse of a square matrix
solve           Solve a linear system of equations
det             Determinant of a square matrix
slogdet         Logarithm of the determinant of a square matrix
lstsq           Solve linear least-squares problem
pinv            Pseudo-inverse (Moore-Penrose) calculated using a singular
                value decomposition
matrix_power    Integer power of a square matrix
matrix_rank     Calculate matrix rank using an SVD-based method
==========================================================
Eigenvalues and decompositions

eig             Eigenvalues and vectors of a square matrix
eigh            Eigenvalues and eigenvectors of a Hermitian matrix
eigvals         Eigenvalues of a square matrix
eigvalsh        Eigenvalues of a Hermitian matrix
qr              QR decomposition of a matrix
svd             Singular value decomposition of a matrix
cholesky        Cholesky decomposition of a matrix
==========================================================
Tensor operations

tensorsolve     Solve a linear tensor equation
tensorinv       Calculate an inverse of a tensor
==========================================================
Exceptions

LinAlgError     Indicates a failed linear algebra operation

3.案例——随机漫步

　

三、pandas基础

1.Series对象