算法的时间复杂度与空间复杂度

算法的时间复杂度

　　事前估算方法：通过分析某个算法的时间复杂度来判断那个算法更优。

　　事后统计方法：这种方法可行，但不是一个好的方法。该方法有两个缺陷：一是要想对设计的算法的运行性能进行评测，必须先依据算法编制相应的程序并实际运行；二是所得时间的统计量依赖于计算机的硬件、软件等环境因素，有时容易掩盖算法本身的优势。

　　时间频度：一个算法花费的时间与算法中语句的执行次数成正比，那个算法中语句执行的次数多，它所花费的时间就多。一个算法中的语句执行次数称为语句频度或时间频度。记为T(n)。

　　时间复杂度：

　　1.一般情况下，算法的基本操作语句的重复执行次数是问题规模n的某个函数，用T(n)表示，若有某个辅助函数f(n),使得当n趋近于无穷大时，T(n)/f(n)的极限值不等于零的常数，则称f(n)是T(n)的同数量级函数。记作T(n)=O(f(n)),称O(f(n))为算法的渐进时间复杂度，简称时间复杂度。

　　2.T(n)不同，但时间复杂度可能相同。如：T(n)=n²+7n+6与T(n)=3n²+2n+2他们的T(n)不同，但时间复杂度相同，都为O(n²)。

　　3.计算时间复杂度的方法

　　　　1)用常数1代替运行时间中所有加法常数 T(n)=6n²+7n+6=>T(n)=6n²+7n+1

　　　　2)修改后的运行次数函数中，只保留最高阶项 T(n)=6n²+7n+1=>T(n)=6n²

　　　　3)去除最高阶项的系数 T(n)=6n²=>T(n)=n²=>O(n²)

常见的时间复杂度

1.常数阶O(1)：不管代码执行了多少行，只要代码没有循环等复杂结构，那么该代码的时间复杂度就是O(1)　　　

int i=1;
int j=2;
i++;
j++;
int sum=i+j;

此类代码在执行的过程中，他所消耗的时间并不会随着变量的增大而增长，因此，无论代码有多长，都可以用O(1)来表示他的时间复杂度

2.对数阶O(log₂n)

int i=1;
while(i<n){
i=2*i; 
}

每执行一次循环，i的值距离n就越近，假设执行x次后，2^x=n,那么x=log2n，也就是说，当循环log2n次，此代码就结束了，所以这个代码的时间复杂度为：O(log2n) 根据上述规则，当i=i*10,则时间复杂度为O(lgn)，依次类推。

3.线性阶O(n)

for(int i=1;i<=n;i++){
       i++; 
}

for循环里的代码会执行n遍，他所消耗的时间是随着n的变化而变化的，因此可以用O(n)来表示他的时间复杂度

4.线性对数阶Ο(nlog₂n)

for(i=1;i<n;i++){
    int j=1;
     while(j<n){
         i=2*i
  }      
}

^{线性对数阶Ο(nlog₂n)其实很好理解，就是在对数阶Ο(log₂n)的代码基础上，循环执行n遍，那么他的时间复杂度即为Ο(nlog₂n)}

5.平方阶Ο(n²)

for(int x=1;i<=n;i++){
    for(int j=1;j<=n;j++){
         j=i;
         j++
     }   
}

在循环执行n次的基础上，嵌套一次n次循环，即执行了n*n次，此时它的时间复杂度就是Ο(n²)

6.立方阶O(n³)

在Ο(n²)的基础上，内部再嵌套一次循环

7.K次方阶O(n^k)

嵌套k次循环，且每层循环执行n次

8.指数阶O(2ⁿ)

 同上理解

常见的时间复杂度对应的图

 

 

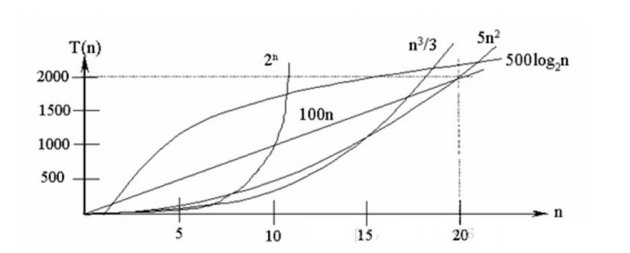
 　　常见的算法时间复杂度由小到大依次为：Ο(1)＜Ο(log₂n)＜Ο(n)＜Ο(nlog₂n)＜Ο(n²)＜Ο(n³)＜…＜Ο(2ⁿ)＜Ο(n!)

　　由图可知：我们应该尽量避免使用指数阶的算法，可以多选用对数阶

平均时间复杂度与最坏时间复杂度

 1.平均时间复杂度是指所有可能的输入实例均以等概率出现的情况下，该算法的运行时间

 2.最坏情况下的时间复杂度称最坏时间复杂度。一般讨论的时间复杂度均是最坏情况下的时间复杂度，这样做的原因是：最坏的情况下的时间复杂度在任何输入实例上的运行时间的界限，这就保证了算法的运行时间不会比最坏情况更长

 3.平均时间复杂度和最坏时间复杂度是否一致和算法有关，如下图：

 

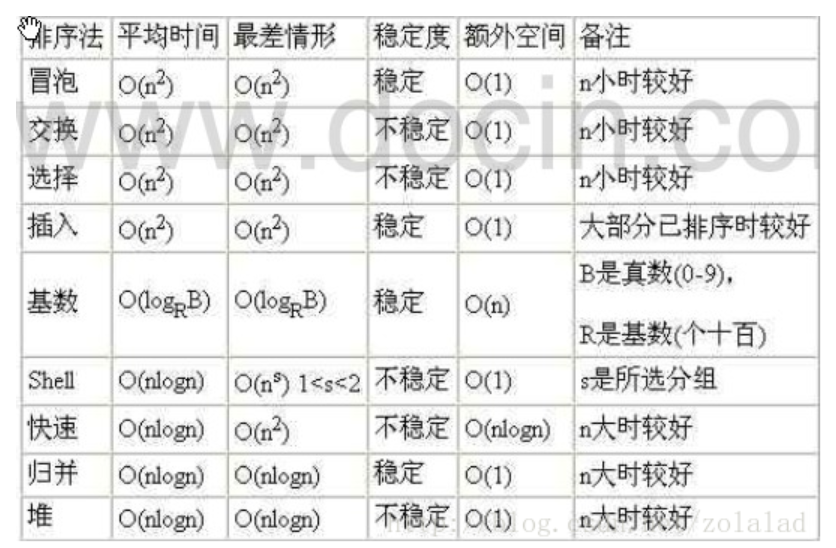
 算法的空间复杂度

　　类似于时间复杂度的讨论，一个算法的空间复杂度(Space Complexity)S(n)定义为该算法所耗费的存储空间，它也是问题规模n的函数。渐近空间复杂度也常常简称为空间复杂度。
　　空间复杂度(Space Complexity)是对一个算法在运行过程中临时占用存储空间大小的量度。有的算法需要占用的临时工作单元数与解决问题的规模n有关，它随着n的增大而增大，当n较大时，将占用较多的存储单元，例如快速排序和归并排序算法就属于这种情况。

　　在做算法分析时，我们注意讨论的是时间复杂度。从用户的使用体验上看，更看重的是程序执行的速度，一些缓存产品（redis,memcahe）和算法（基数排序）的本质就是使用空间换时间。