逆波兰表达式完整实现

　　上篇中，我们只支持对整数实现，本篇完整实现，支持加减乘除和多位数、小数，思路与上篇相同。

因此直接上代码实现过程

package com.atxihua;

import java.util.ArrayList;
import java.util.Collections;
import java.util.List;
import java.util.Stack;
import java.util.regex.Pattern;

public class reversePolishMultiCalc {
    public static void main(String[] args) {
        String math="12.8+(2 - 3.55)*4+10/5.0";//去除空格，故意在-前后添加空格进行测试
        try {
            doCalc(doMatch(math));
        } catch (Exception e) {
            e.printStackTrace();
        }
    }
    /*
    * 匹配+ - * / ()运算符
    * */
    static final String SYMBOL="\\+|-|\\*|/|\\(|\\)";

    static final String LEFT="(";
    static final String RIGHT=")";
    static final String ADD="+";
    static final String MINUS="-";
    static final String TIMES="*";
    static final String DIVISON="/";

    static final int LEVEL_01=1;//+ -
    static final int LEVEL_02=2;//* /
    static final int LEVEL_HIGH=Integer.MAX_VALUE;//括号

    static Stack<String> stack=new Stack<>();
    static List<String> data= Collections.synchronizedList(new ArrayList<String>());

    /*
    * 去除所有空白
    * */

public static String replaceAllBlack(String s){
  //\\s+匹配任何空白字符，包括空格、制表符、换页符等待，等价于[\f\n\r\t\v]
  return s.replaceAll("\\s+","") ;
}
//判断是不是数字
public static boolean isNumber(String s){
        Pattern pattern=Pattern.compile("^[-\\+]?[.\\d]*$");
        return  pattern.matcher(s).matches();
    }
//判断是不是运算符
public static boolean isSymbol(String s){
    return s.matches(SYMBOL);
    }
//匹配运算等级
public static int calcLevel(String s){
        if("+".equals(s)||"-".equals(s)){
            return LEVEL_01;
        }else if("*".equals(s)||"/".equals(s)){
            return LEVEL_02;
        }else {
            return LEVEL_HIGH;
        }
    }
public static List<String> doMatch(String s){
        if(s==null||"".equals(s.trim()))throw new RuntimeException("data is empty");
        //进行简单校验，保证第一个是数字
        if(!isNumber(s.charAt(0)+""))throw new RuntimeException("data is illeagle,start not with a number");
        s=replaceAllBlack(s);
        String each;
        int start=0;
        for(int i=0;i<s.length();i++){
            if(isSymbol(s.charAt(i)+"")){
                each=s.charAt(i)+"";
               //栈为空，(操作符，或者操作符优先级大于栈顶优先级&&操作符优先级不是()优先级及是 ) 不能直接入栈
                if(stack.isEmpty()||LEFT.equals(each)
                ||((calcLevel(each)>calcLevel(stack.peek()))&&calcLevel(each)<LEVEL_HIGH)){
                    stack.push(each);
                }else if(!stack.isEmpty()&&calcLevel(each)<=calcLevel(stack.peek())){
                    //栈非空，操作符优先级小于等于栈顶优先级时出栈入列，直到栈为空，或者遇到(,最后操作符入栈
                    while (!stack.isEmpty()&& calcLevel(each)<=calcLevel(stack.peek())){
                        if(calcLevel(stack.peek())==LEVEL_HIGH){
                            break;
                        }
                        data.add(stack.pop());
                    }
                    stack.push(each);
                }else if(RIGHT.equals(each)){
                    //)操作符，依次出栈入列直到空栈或者遇到第一个)操作符，此时)出栈
                    while (!stack.isEmpty()&&LEVEL_HIGH>=calcLevel(stack.peek())){
                        if(LEVEL_HIGH==calcLevel(stack.peek())){
                            stack.pop();
                            break;
                        }
                        data.add(stack.pop());
                    }
                }
                start=i;
            }else if(i==s.length()-1||isSymbol(s.charAt(i+1)+"")){
                each=start==0?s.substring(start,i+1):s.substring(start+1,i+1);
                if(isNumber(each)){
                    data.add(each);
                    continue;
                }
                throw new RuntimeException("data not match number");
            }
        }
        //如果栈里还有元素，此时元素需要依次出栈入列，可以想象栈里剩下栈顶为/，栈底为+，应该依次出栈入列
        //可以直接反转整个stack添加到队列中
        Collections.reverse(stack);
        data.addAll(new ArrayList<>(stack));
        System.out.println(data);
        return data;
     }
//计算结果
public static Double doCalc(List<String> list){
    Double d=0d;
    if(list==null||list.isEmpty()){
        return null;
    }
    if(list.size()==1){
        System.out.println(list);
        d=Double.valueOf(list.get(0));
        return d;
    }
    ArrayList<String> list1=new ArrayList<>();
    for(int i=0;i<list.size();i++){
        list1.add(list.get(i));
        if(isSymbol(list.get(i))){
            Double d1=doTheMath(list.get(i-2),list.get(i-1),list.get(i));
            list1.remove(i);
            list1.remove(i-1);
            list1.set(i-2,d1+"");
            list1.addAll(list.subList(i+1,list.size()));
            break;
        }
    }
    doCalc(list1);
    return d;
}
//运算
    public static Double doTheMath(String s1, String s2, String symbol) {
    Double result;
    switch (symbol){
        case ADD:result=Double.valueOf(s1)+Double.valueOf(s2);break;
        case MINUS:result=Double.valueOf(s1)-Double.valueOf(s2);break;
        case TIMES:result=Double.valueOf(s1)*Double.valueOf(s2);break;
        case DIVISON:result=Double.valueOf(s1)/Double.valueOf(s2);break;
        default:result=null;
    }
    return result;
    }
}

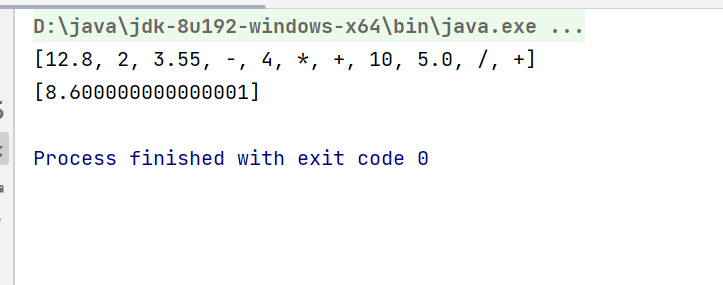
运行结果：