关于单调性优化DP算法的理解
Part1-二分栈优化DP
引入
二分栈主要用来优化满足决策单调性的DP转移式。
即我们设\(P[i]\)为\(i\)的决策点位置,那么\(P[i]\)满足单调递增的性质的DP。
由于在这种DP中,满足决策点单调递增,那么对于一个点来说,以它为决策点的点一定是一段连续的区间。
所以我们可以枚举以哪个点作为决策点,去找到它所对应的以它为决策点的区间。
考虑如何找到一个点的区间:
可以发现,在当前情况下(枚举到以某个点作为决策点的情况下),该点所对应的区间一定为[L,N].(L可能等于N+1)
那么我们可以用一个栈来存储区间[L,N]中的L,每次新枚举到一个决策点\(i\),就用栈顶L判断,看L是用原决策点更优,还是用新决策点\(i\)更优。
因为满足决策单调性,所以若用新决策点更优的话,该L就没有意义了,就直接可以从栈顶弹出。
我们一直执行以上操作,直到遇到一个L的原决策点比新决策点\(i\)更优,那么说明这个L还是有意义的,所以不能弹。
然后我们就需要去二分一个点出来作为新的L,使得这个点右边的点以\(i\)为决策点更优,左边的点以\(i\)为决策点更劣。
以上就是二分栈的基本思路。
举个例子:
决策点:1111111111 栈:1(1)
决策点:1112222222 栈:1(1) 4(2)
决策点:1112222233 栈:1(1) 4(2) 9(3)
决策点:1112224444 栈:1(1) 4(2) 7(4)
注:栈里应该有两个信息,一个是L,一个是转移点.
(我们不能维护每个点的转移点,那样会提高时间复杂度)
代码实现思路:
①定义一个队首指针,对于目前枚举到的决策点\(i\),若\(i\)未被队首指针的区间包含,那么指针前移,直到\(i\)被包含,然后更新\(i\)的DP值。(\(i\)的决策点就是目前队首指针所对应的转移点)
②判断目前栈顶的L以\(i\)为决策点更优,还是以原决策点更优。若以\(i\)更优,弹出栈顶,然后,循环往复②操作。
③对于目前的栈,判断一下,栈是否为空:
- 若为空,直接让新的信息入栈。
- 若不为空,二分新决策点L的位置(此处所有点的原决策点都是目前栈顶的原决策点),入栈。
(注:记得特判L!=N+1)
小结
对于大多关于二分栈的题,一般是发现有单调性后就直接套版了。
所以在使用二分栈时,一般需要先证明DP的决策单调性(一般使用打表法证明),限制还是很大。
注:有转移限制的DP对二分栈限制很大,只有在限制也满足单调性的情况下才能用。
(比如CSP2019D2T2划分就可以用类二分栈做法过掉\(O(N*log(N))\)能过的所有点)
#include<cstdio>
#include<algorithm>
using namespace std;
const long long ONE=1;
const int MOD=(1<<30);
const int MAXM=100005;
const int MAXN=40000005;
const long long INF=4e18;
int N,TYP,Pt[MAXN];
long long A[MAXN],Dp[MAXN];
int Stac[MAXN],ID[MAXN],L,R;
void Prepare(){
scanf("%d%d",&N,&TYP);
if(TYP==1){
int X,Y,Z,M;
int P[MAXM]={0},B[MAXN]={0};
scanf("%d%d%d%d%d%d",&X,&Y,&Z,&B[1],&B[2],&M);
for(int i=3;i<=N;i++)B[i]=(ONE*B[i-1]*X+ONE*B[i-2]*Y+Z)%MOD;
for(int i=1,L,R;i<=M;i++){
scanf("%d%d%d",&P[i],&L,&R);
for(int j=P[i-1]+1;j<=P[i];j++)
A[j]=B[j]%(R-L+1)+L;
}
return ;
}
for(int i=1;i<=N;i++)
scanf("%lld",&A[i]);
}
int main(){
Prepare();
for(int i=1;i<=N;i++)
A[i]=A[i-1]+A[i];
for(int i=1;i<=N;i++){
while(Stac[L+1]<=i&&L<R)L++;
long long x=A[i]-A[ID[L]];
Dp[i]=Dp[ID[L]]+x*x;Pt[i]=ID[i];
int l=i,r=N+1;
while(L<=R&&A[Stac[R]]-A[i]>=x)R--;
if(L>R){Stac[++R]=i+1;ID[R]=i;continue;}
while(l+1<r){
int mid=(l+r)/2;
if(x<=A[mid]-A[i])r=mid;
else l=mid;
}
if(r==N+1)continue;
Stac[++R]=r;ID[R]=i;
}
printf("%lld\n",Dp[N]);
}
例题
其实主要是证单调性,其它的部分都比较版。
T1玩具装箱
(虽说这是个斜率优化板题呢...)
最终核心大意:给出了\(P\)数组与一个常数\(L\),其中\(P\)数组满足单调递增的性质。
有一个Dp转移式:\(Dp[i]=min\{Dp[j]+(P[i]-P[j]-L)^2\};\)
单调性证明如下:
采用反证:设有\(A,B,C,D(A<B<C<D)\),其中\(A\)为\(D\)的最优决策点,\(B\)为\(C\)的最优决策点。(即要证明这种情况不存在)
那么有$$Dp[A]+(P[D]-P[A]-L)^2\le Dp[B]+(P[D]-P[B]-L)^2$$
可以得到:
化简得:
与条件不符,故不存在这种情况,即证明该Dp有决策单调性。
#include<cstdio>
#include<string>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
const int MAXN=50005;
int N,Len,A[MAXN],Pt[MAXN];
long long S[MAXN],Dp[MAXN];
int Stac[MAXN],ID[MAXN],L,R;
long long W(int i,int j){
return (S[i]-S[j]-Len)*(S[i]-S[j]-Len);
}
int main(){
scanf("%d%d",&N,&Len);Len++;
for(int i=1;i<=N;i++)
scanf("%d",&A[i]),S[i]=S[i-1]+A[i];
for(int i=1;i<=N;i++)S[i]+=i;
for(int i=1;i<=N;i++){
while(Stac[L+1]<=i&&L<R)L++;
Dp[i]=Dp[ID[L]]+W(i,ID[L]);
while(L<=R&&Dp[ID[R]]+W(Stac[R],ID[R])>=Dp[i]+W(Stac[R],i))R--;
if(R<L)Stac[++R]=i+1,ID[R]=i;
else{
int l=i,r=N+1;
while(l+1<r){
int mid=(l+r)/2;
if(Dp[ID[R]]+W(mid,ID[R])>=Dp[i]+W(mid,i))r=mid;
else l=mid;
}
if(r==N+1)continue;
Stac[++R]=r;ID[R]=i;
}
}
printf("%lld\n",Dp[N]);
return 0;
}
/*
Dp[i]=Min{Dp[j]+W(i,j)};
*/
T2诗人小G
最终核心大意:给出了\(P\)数组与一个常数\(L\)及一个参数\(K\),其中\(P\)数组满足单调递增的性质。
有一个Dp转移式:\(Dp[i]=min\{Dp[j]+|P[i]-P[j]-L|^K\};\)
单调性证明如下:(沿用T1的思路)
采用反证:设有\(A,B,C,D(A<B<C<D)\),其中\(A\)为\(D\)的最优决策点,\(B\)为\(C\)的最优决策点。(即要证明这种情况不存在)
那么有$$Dp[A]+|P[D]-P[A]-L|^K\le Dp[B]+|P[D]-P[B]-L|^K$$
可以得到:
然后......
我们设\(X=P[B]-P[A],Y=P[C]-P[B],Z=P[D]-P[C];\)
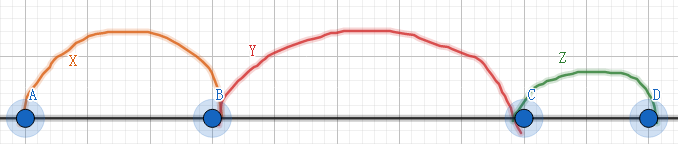
那么有:$$|X+Y+Z-L|K+|Y-L|K\le |Y+Z-L|K+|X+Y-L|K$$
我们不妨画出\(F(t)=|t-L|^K\)的图像,就像这样:
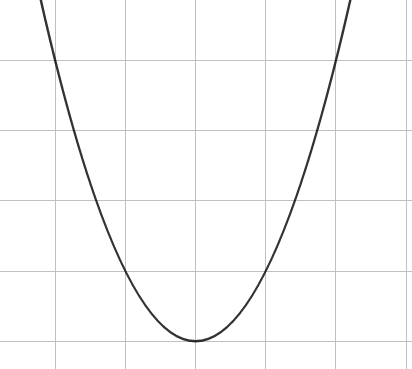
然后在图像上将那四个点标出来。
发现\((X+Y+Z-L)+(Y-L)=(Y+Z-L)+(X+Y-L)\),即这四个点的横坐标是关于\(E=\frac{X+2*Y+Z}{2}\)对称的。
但由于那四个点的分布情况繁多,所以不妨分类讨论(由于左边右边本质是一样的,所以这里只讨论一边的情况):
①:左二右二(左边两个点,右边两个点)

这种情况下,显然\(F(Y)+F(X+Y+Z)\ge F(X+Y)+F(Y+Z)\)
故与条件不符。
②:左一右三(左边一个点,右边三个点)
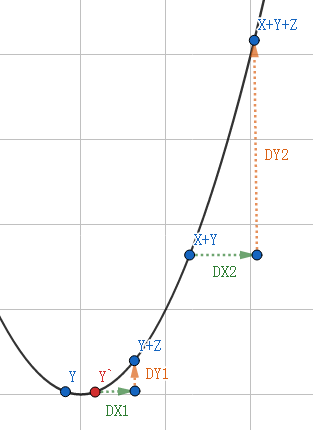
那么这种情况下,我们将\(Y\)翻转至\(Y`\),那么此时有\(DX1<DX2,DY1<DY2\),即$$F(Y+Z)-F(Y)=F(Y+Z)-F(Y`)<F(X+Y+Z)-F(X+Y)$$
即有$$F(Y+Z)+F(X+Y)<F(X+Y+Z)+F(Y)$$
故与条件不符。
③:左零右四(左边零个点,右边四个点)
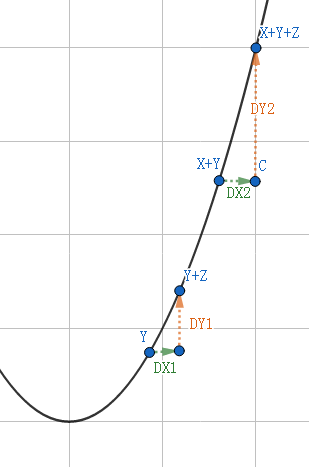
这种情况下有\(DX1=DX2\),由函数斜率递增的性质可得\(DY1<DY2\)
故同②的情况,与条件不符。
综上,不存在给出情况,故该Dp式满足决策单调性。
(证完单调性后就和玩具装箱一样了,故这里就不给代码了 )
Part2-分治优化DP
引入
其实也没啥好引入的
约束:一般在使用分治优化的时候,DP是满足决策单调性的。
对于形同$$Dp1[i]=max/min{Dp2[j]+W(i,j)};$$这样的DP式子,我们一般是在\(O(N^2)\)出解。(即枚举一个\(i\),一个\(j\))
但是由于满足决策单调性,我们可以这样想:
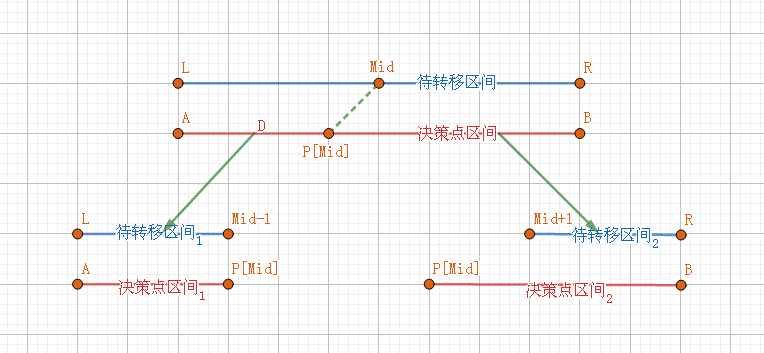
对于\(Dp1\)来说,我们设待转移区间(\(i\))即未更新区间为\([L,R]\),
设目前可从\(Dp2\)转移过来的点构成的区间(\(j\))即决策点区间为\([A,B]\).
对于普通的转移,我们第一步会枚举一个\(Dp1[i]\)出来进行转移,
但是现在,我们可以使\(i\)变为当前需转移区间\([L,R]\)的中心点\(Mid=\frac{L+R}{2}\),
即每次转移只转移\(Dp1[Mid]\),并顺便找出\(Dp1[Mid]\)的决策点\(P[Mid]\).
之后,我们可以把待转移区间\([L,R]\)分为两半:\([L,Mid-1]\)和\([Mid+1,R]\).
而又由于,我们的\(DP\)是满足决策单调性的,所以决策点区间也可以分成两半:\([A,P[Mid]]\)与\([P[Mid],B]\).
然后就可以递推下去了。
又由于我们的DP是满足决策单调性的,所以正确性可以保证。
而在每一层内,决策点总共被枚举次数是\(O(N)\)的,一共有\(log(N)\)层。
故总的时间复杂度是\(O(N*log(N))\).
例题
主要还是证单调性。
T1Ciel and Gondolas
题意,有\(N\)个人,每两个人\(i,j\)之间有\(A[i][j]\)的怨气值。
定义一个组的怨气和为该组内任意两个人的怨气值之和。
现要求将这\(N\)个人分成\(K\)组,使得这\(K\)组的怨气和最小。
问最小怨气和。
好吧,最终DP式子就是:
单调性的话,证明其实比较简单,这里就不赘述了。
#include<cstdio>
#include<algorithm>
using namespace std;
const int MAXN=4005;
const int INF=0X3F3F3F3F;
int N,K,A[MAXN][MAXN];
int Dp[MAXN][MAXN];
int Pt[MAXN][MAXN];
inline int Read(){
register int x=0;
char c=getchar();bool f=0;
while(c<'0'||c>'9'){if(c=='-')f^=1;c=getchar();}
while(c>='0'&&c<='9'){x=(x<<1)+(x<<3)+(c-'0');c=getchar();}
if(f==1)x=-x;return x;
}
int W(int i,int j){
return A[i][i]-A[i][j-1]-A[j-1][i]+A[j-1][j-1];
}
void Solve(int k,int l,int r,int pl,int pr){
if(l>r)return ;
int mid=(l+r)/2,pt=pl;
Dp[k][mid]=INF;
for(int i=pl;i<=min(mid,pr);i++){
int cost=Dp[k-1][i-1]+W(mid,i);
if(cost<Dp[k][mid])Dp[k][mid]=cost,pt=i;
}
Solve(k,l,mid-1,pl,pt);
Solve(k,mid+1,r,pt,pr);
}
int main(){
N=Read();K=Read();
for(int i=1;i<=N;i++)
for(int j=1;j<=N;j++){
A[i][j]=Read();
A[i][j]+=A[i][j-1]+A[i-1][j]-A[i-1][j-1];
}
for(int i=1;i<=N;i++)Dp[0][i]=INF;
for(int k=1;k<=K;k++)Solve(k,1,N,1,N);
printf("%d\n",Dp[K][N]/2);
}
T2The Bakery
题意,给出\(N\)个数,现让你将这\(N\)个数划分为\(K\)段,
定义某一段的代价为该段内不同元素的个数,求最大总代价。
通过以上描述,易得最终DP式为:
其中\(W(i,j)\)表示\([j,i]\)中不同的数的个数。
关于这个DP式的单调性,我们可以这样想:
设有\(A,B,C,D(A<B<C<D)\)四个数,
其中\(A\)为\(D\)的最优决策点,\(B\)为\(C\)的最优决策点。
那么相应的,就有
即有:
我们可以这样想,将\([A,D]\)这个区间分成如下几个部分:
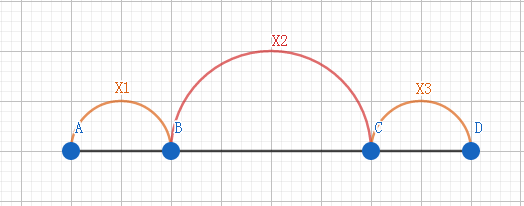
其中\(X2\)表示\(W(C,B)\)的值,
而\(X1,X3\)分别表示\([A,B],[C,D]\)中与\([B,C]\)间不同的数。
即:\(X1+X2=W(C,A),X3+X2=W(D,B)\)
那么$$W(D,A)+W(C,B)>W(C,A)+W(D,B)$$
这个式子就可以写作:
而上式显然不成立,故该DP满足决策单调性。
讨论了DP的决策单调性,那么是否可以直接套用之前的板呢?
然而不行,发现在以下板块时:
void Solve(int k,int l,int r,int pl,int pr){
if(l>r)return ;
int mid=(l+r)/2,pt=pl;
Dp[k][mid]=-INF;
for(int i=pl;i<=min(mid,pr);i++){
int cost=Dp[k-1][i-1]+W(mid,i);
if(cost>=Dp[k][mid])Dp[k][mid]=cost,pt=i;
}
Solve(k,l,mid-1,pl,pt);
Solve(k,mid+1,r,pt,pr);
}
我们算\(W(mid,i)\)无法\(O(1)\)出解,同时有一个处理思路就是:
void Solve(int k,int l,int r,int pl,int pr){
if(l>r)return ;
int mid=(l+r)/2,pt=pl;
Dp[k][mid]=-INF;
for(int i=mid;i>pr;i--)Tur(i);
for(int i=min(mid,pr);i>=pl;i--){
Tur(i);int cost=Dp[k-1][i-1]+Cnt;
if(cost>=Dp[k][mid])Dp[k][mid]=cost,pt=i;
}
Solve(k,l,mid-1,pl,pt);
Solve(k,mid+1,r,pt,pr);
}
其中,Tur(i)表示更新某一元素入答案中。
但是这样做会多增加\([pr+1,mid]\)的循环,从而增加时间复杂度。
从而被恶意出题人卡成TLE...
针对于以上情况,我们可以使用一种类似于滑动的思想。
即使用两个指针\(L,R\),然后维护区间\(W(L,R)\)的值。
每次要求某个\(W(l,r)\)的时候,就将\(L\)滑动到\(l\),\(R\)滑动到\(r\),滑动途中维护\(W(L,R)\)就行了。
void Tur(int x,int k){
CCnt[Val[x]]+=k;
if(CCnt[Val[x]]==0&&k==-1)Cnt--;
if(CCnt[Val[x]]==1&&k==1)Cnt++;
}
long long W(int r,int l){
while(L>l)Tur(--L,1);
while(R<r)Tur(++R,1);
while(L<l)Tur(L++,-1);
while(R>r)Tur(R--,-1);
return Cnt;
}
void Solve(int k,int l,int r,int pl,int pr){
if(l>r)return ;
int mid=(l+r)/2,pt=pl;
Dp[k][mid]=-INF;
for(int i=min(mid,pr);i>=pl;i--){
long long cost=Dp[k-1][i-1]+W(mid,i);
if(cost>=Dp[k][mid])Dp[k][mid]=cost,pt=i;
}
Solve(k,l,mid-1,pl,pt);
Solve(k,mid+1,r,pt,pr);
}
而这样的时间复杂度也是\(O(N*log(N))\)的。
原因如下:
首先,由于我们函数的递推结构是先左再右,
所以我们的\(L\)指针移动的总步数是\(O(N)\)范围的。
同时,我们每次走的区间都是连续的,而对于任意一个位置,我们最多只会经过\(O(log(N))\)次。
所以,时间复杂度还是\(O(N*log(N))\)的。
#include<cstdio>
#include<algorithm>
using namespace std;
const int MAXK=55;
const int MAXN=35005;
const long long INF=1e18;
int T,N,K,L,R,Ans;
int Val[MAXN],Cnt,CCnt[MAXN];
long long Dp[MAXK][MAXN];
inline int Read(){
register int x=0;
char c=getchar();bool f=0;
while(c<'0'||c>'9'){if(c=='-')f^=1;c=getchar();}
while(c>='0'&&c<='9'){x=(x<<1)+(x<<3)+(c-'0');c=getchar();}
if(f==1)x=-x;return x;
}
void Tur(int x,int k){
CCnt[Val[x]]+=k;
if(CCnt[Val[x]]==0&&k==-1)Cnt--;
if(CCnt[Val[x]]==1&&k==1)Cnt++;
}
long long W(int r,int l){
while(L>l)Tur(--L,1);
while(R<r)Tur(++R,1);
while(L<l)Tur(L++,-1);
while(R>r)Tur(R--,-1);
return Cnt;
}
void Solve(int k,int l,int r,int pl,int pr){
if(l>r)return ;
int mid=(l+r)/2,pt=pl;
Dp[k][mid]=-INF;
for(int i=min(mid,pr);i>=pl;i--){
long long cost=Dp[k-1][i-1]+W(mid,i);
if(cost>=Dp[k][mid])Dp[k][mid]=cost,pt=i;
}
Solve(k,l,mid-1,pl,pt);
Solve(k,mid+1,r,pt,pr);
}
int main(){
N=Read();K=Read();
for(int i=1;i<=N;i++)Val[i]=Read();
for(int i=1;i<=N;i++)Dp[0][i]=-INF;
for(int k=1;k<=K;k++)Solve(k,1,N,1,N);
printf("%lld\n",Dp[K][N]);
}
后记
打表法好啊。。。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号