二叉树

简介
二叉树（Binary tree）是树形结构的一个重要类型。许多实际问题抽象出来的数据结构往往是二叉树形式，即使是一般的树也能简单地转换为二叉树，而且二叉树的存储结构及其算法都较为简单，因此二叉树显得特别重要。二叉树特点是每个结点最多只能有两棵子树，且有左右之分。
如果该二叉树的所有叶子节点都在最后一层，并且结点总数= 2^n -1 , n 为层数，则我们称为满二叉树。
如果该二叉树的所有叶子节点都在最后一层或者倒数第二层，而且最后一层的叶子节点在左边连续，倒数第二层的叶子节点在右边连续，我们称为完全二叉树。
为什么需要树这种数据结构？
能提高数据存储，读取的效率, 比如利用 二叉排序树(Binary Sort Tree)，既可以保证数据的检索速度，同时也可以保证数据的插入，删除，修改的速度。
示意图

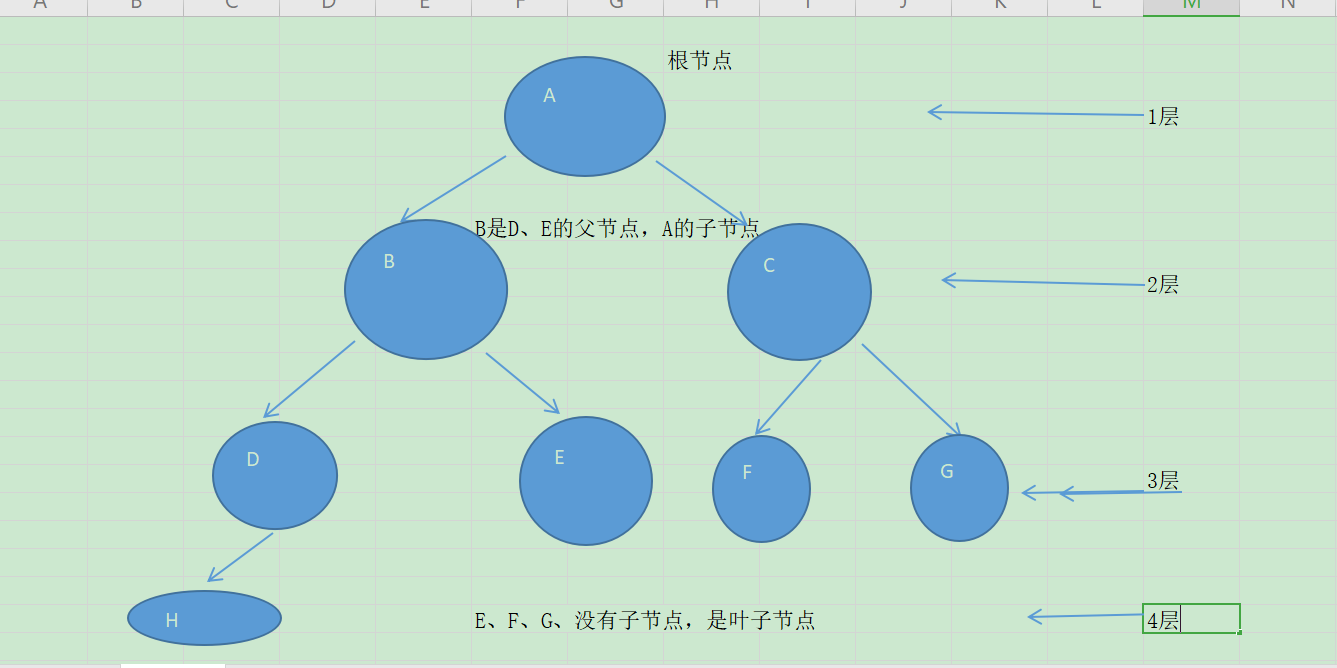
树的常用术语

1. 结点
2. 根结点
3. 父结点
4. 子结点
5. 叶子结点（无子结点的结点）
6. 结点的权（结点值）
7. 路径（从root节点找到该结点的路线）
8. 层
9. 子树
10. 树的高度
11. 森林 :多颗子树构成森林
    二叉树遍历
12. 前序遍历：先输出父结点，再输出左结点和右结点
13. 中序遍历：先输出左结点，再输出父结点和右结点
14. 后序遍历：先输出左结点和右结点，再输出父结点
    其实就是看父节点输出的顺序
    代码
    结点对象

class Node {
  int value;

  public Node(int value) {
    this.value = value;
  }

  Node left;
  Node right;

  @Override
  public String toString() {
    return "Node{" +
            "value=" + value +
            '}';
  }

public void add(Node node) {
    if (node == null) {
      return;
    }
    if (this.value > node.value) {
      if (this.left == null) {
        this.left = node;
      } else {
        this.left.add(node);
      }
    } else {
      if (this.right == null) {
        this.right = node;
      } else {
        this.right.add(node);
      }
    }
  }

  //前序遍历
  public void preorder() {
    System.out.println(this);
    if (this.left != null) {
      this.left.preorder();
    }
    if (this.right != null) {
      this.right.preorder();
    }
  }

  //中序遍历
  public void inorder() {
    if (this.left != null) {
      this.left.inorder();
    }
    System.out.println(this);
    if (this.right != null) {
      this.right.inorder();
    }
  }

  //后序遍历
  public void postorder() {
    if (this.left != null) {
      this.left.postorder();
    }
    if (this.right != null) {
      this.right.postorder();
    }
    System.out.println(this);
  }
  
}

树

class BinaryTree {
  private Node root;

public void add(Node node) {
    if (root == null) {
      root = node;
    } else {
      root.add(node);
    }
  }


  //前序遍历
  public void preorder() {
    if (root != null) {
      root.preorder();
    } else {
      System.out.println("二叉树为空");
    }
  }

  //中序遍历
  public void inorder() {
    if (root != null) {
      root.inorder();
    } else {
      System.out.println("二叉树为空");
    }
  }

  //后序遍历
  public void postorder() {
    if (root != null) {
      root.postorder();
    } else {
      System.out.println("二叉树为空");
    }
  }

}

动态添加结点，比父结点大的添加到左结点，比父结点小的添加到右结点（二叉排序树）
测试

    BinaryTree binaryTree = new BinaryTree();
    int[] arr = {1,7,2,5,9,6};
    for (int i : arr) {
      binaryTree.add(new Node(i));
    }
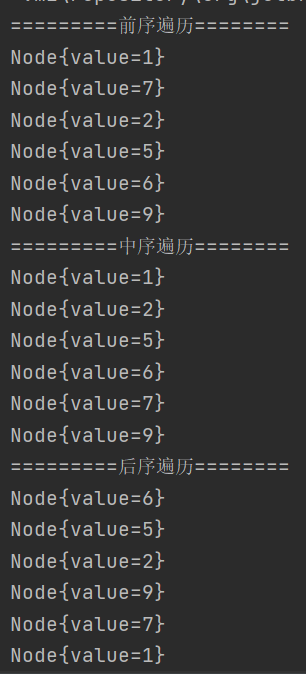
    System.out.println("=========前序遍历========");
    binaryTree.preorder();
    System.out.println("=========中序遍历========");
    binaryTree.inorder();
    System.out.println("=========后序遍历========");
    binaryTree.postorder();

查找指定结点
结点对象代码

 /**
   * 前序查找
   * @param value 查找值为value的结点
   * @return 如果找到就返回该结点，找不到返回null
   */
  public Node preorderSearch(int value) {
    if (this.value == value) {
      return this;
    }
    Node node = null;
    if (this.left != null) {
      node = this.left.preorderSearch(value);
    }
    if (node != null) {
      return node;
    }
    if (this.right != null) {
      node = this.right.preorderSearch(value);
    }
    return node;
  }

  /**
   * 中序查找
   * @param value 查找值为value的结点
   * @return 如果找到就返回该结点，找不到返回null
   */
  public Node inorderSearch(int value) {
    Node node = null;
    if (this.left != null) {
      node = this.left.inorderSearch(value);
    }
    if (node != null) {
      return node;
    }
    if (this.value == value) {
      return this;
    }
    if (this.right != null) {
      node = this.right.inorderSearch(value);
    }
    return node;
  }

  /**
   * 后序查找
   * @param value 查找值为value的结点
   * @return 如果找到就返回该结点，找不到返回null
   */
  public Node postorderSearch(int value) {
    Node node = null;
    if (this.left != null) {
      node = this.left.postorderSearch(value);
    }
    if (node != null) {
      return node;
    }
    if (this.right != null) {
      node = this.right.postorderSearch(value);
    }
    if (node != null) {
      return node;
    }
    if (this.value == value) {
      return this;
    }
    return null;
  }

树代码

 /**
   * 前序查找
   * @param value 查找值为value的结点
   * @return 如果找到就返回该结点，找不到返回null
   */
  public Node preorderSearch(int value) {
    if (root != null) {
      return root.preorderSearch(value);
    } else {
      return null;
    }
  }

  /**
   * 中序查找
   * @param value 查找值为value的结点
   * @return 如果找到就返回该结点，找不到返回null
   */
  public Node inorderSearch(int value) {
    if (root != null) {
      return root.inorderSearch(value);
    } else {
      return null;
    }
  }

  /**
   * 后序查找
   * @param value 查找值为value的结点
   * @return 如果找到就返回该结点，找不到返回null
   */
  public Node postorderSearch(int value) {
    if (root != null) {
      return root.postorderSearch(value);
    } else {
      return null;
    }
  }

测试

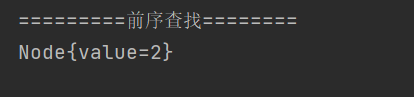
  System.out.println("=========前序查找========");
    Node node = binaryTree.preorderSearch(2);
    if (node != null) {
      System.out.println(node);
    } else {
      System.out.println("没有找到该节点");
    }

删除节点
结点对象代码

 /**
   * @param value 查找值为value的结点
   * @return 找到就返回该结点，找不到返回null
   */
  public Node search(int value) {
    if (value == this.value) {
      return this;
    } else if (value < this.value) {
      if (this.left == null) {
        return null;
      }
      return this.left.search(value);
    } else {
      if (this.right == null) {
        return null;
      }
      return this.right.search(value);
    }
  }

  /**
   * @param value 查找值为value的父节点
   * @return 找到就返回该结点，找不到返回null
   */
  public Node searchParent(int value) {
    if ((this.left != null && this.left.value == value) || (this.right != null && this.right.value == value)) {
      return this;
    } else {
      if (value < this.value && this.left != null) {
        return this.left.searchParent(value);
      } else if (value >= this.value && this.right != null) {
        return this.right.searchParent(value);
      } else {
        return null;
      }
    }
  }

树对象代码

 /**
   * @param value 查找值为value的结点
   * @return 找到就返回该结点，找不到返回null
   */
  public Node search(int value) {
    if (root == null) {
      return null;
    }
    return root.search(value);
  }

  /**
   * @param value 查找值为value的父结点
   * @return 找到就返回该结点，找不到返回null
   */
  public Node searchParent(int value) {
    if (root == null) {
      return null;
    }
    return root.searchParent(value);
  }

  public int delRightTreeMin(Node node) {
    Node temp = node;
    while (temp.left != null) {
      temp = temp.left;
    }
    deleteByStuNo(temp.value);
    return temp.value;
  }

  /**
   * 删除value属性为 value的结点
   * 因为二叉树是单向的，所以我们是判断当前结点的子结点是否需要删除结点，而不能去判断当前这个结点是不是需要删除结点.
   * 如果该结点是叶子结点，直接删除该结点。
   * 如果是非叶子结点：
   * 1.只有一个子结点，用子结点替换该结点
   * 2，有两个结点，取右结点中最小的值替换该结点
   * @param value 被删除结点对象的value
   */
  public void deleteByStuNo(int value) {
    if (root == null) {
      return;
    }
    Node targetNode = search(value);
    if (targetNode == null) {
      return;
    }
    if (root.left == null && root.right == null) {
      root = null;
      return;
    }
    Node parentNode = searchParent(value);
    if (targetNode.left == null && targetNode.right == null) {
      if (parentNode.left != null && parentNode.left.value == value) {
        parentNode.left = null;
      } else if (parentNode.right != null && parentNode.right.value == value) {
        parentNode.right = null;
      }
    } else if (targetNode.left != null && targetNode.right != null) {
      targetNode.value = delRightTreeMin(targetNode.right);
    } else {
      if (targetNode.left != null) {
        if (parentNode != null) {
          if (parentNode.left != null && parentNode.left.value == value) {
            parentNode.left = targetNode.left;
          } else {
            parentNode.right = targetNode.left;
          }
        } else {
          root = targetNode.left;
        }
      } else {
        if (parentNode != null) {
          if (parentNode.left != null && parentNode.left.value == value) {
            parentNode.left = targetNode.right;
          } else {
            parentNode.right =targetNode.right;
          }
        } else {
          root = targetNode.right;
        }
      }
    }
  }

测试

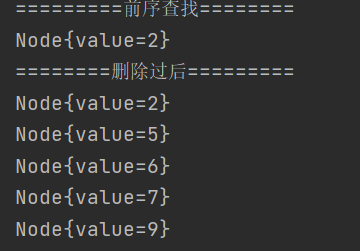
    System.out.println("========删除过后=========");
    binaryTree.deleteByStuNo(1);
    binaryTree.inorder();