C. Heidi and Library （神奇的网络流）

C. Heidi and Library

题意

有 n 种分别具有价格 b 的书 a ，图书馆里最多同时存放 k 本书，已知接下来 n 天每天都有一个人来看某一本书，如果图书馆里没有则需要购买，问最少花费多少钱。

分析

这道题的一个简单版本 ，默认所有书价格为1，那么只需要用 set 维护一下，当图书馆内库存满的时候 erase 掉距离最大的书（贪心做法）。
但是有了价格之后，就不能贪心了，然后这道题就可以用神奇的网络流解决。准确的说是最小费用最大流。
所有边的容量为 1，将 n 个点拆成 2n 个点（2i，2i + 1），2i 和 2i + 1 连边，花费 -INF（因为求的最小费用，这里保证了 n 个点都会经过到），源点 S 连边 2i，费用为 b[a[i]] ，2i + 1 连边汇点 T，费用为 0 。遍历 n 个点，2i + 1 连边 2j ，如果 a[j] == a[i] ，费用为 0，否则费用为 b[a[j]]。
以上就是建图的过程，我们可以把 k 当作网络流的流量，以样例1为例。

4 80 // n k 
1 2 2 1 // 看的书的种类
1 1 1 1 // 价格

当 k = 1 时，

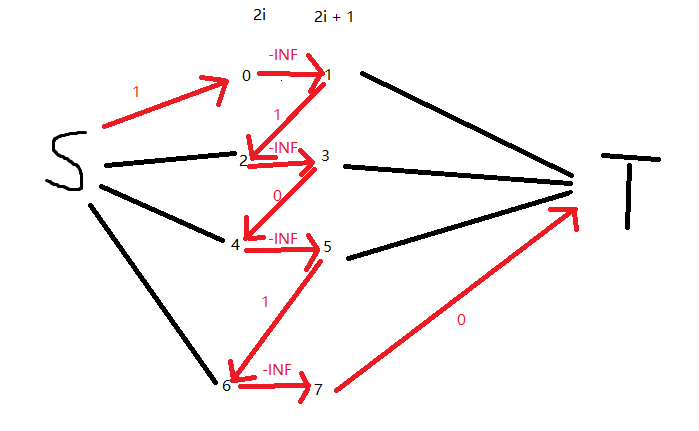
首先最小费用流会保证一次跑完所有费用为 -INF 的边，保证了经过所有点，那么 k = 1 其实就是除非连续的几天种类相同，不然都要扔掉，买另一种书，我们在加边的时候已经处理了，比如相邻的边 (3 -> 4) 费用为 0。这种情况下花费为 3。

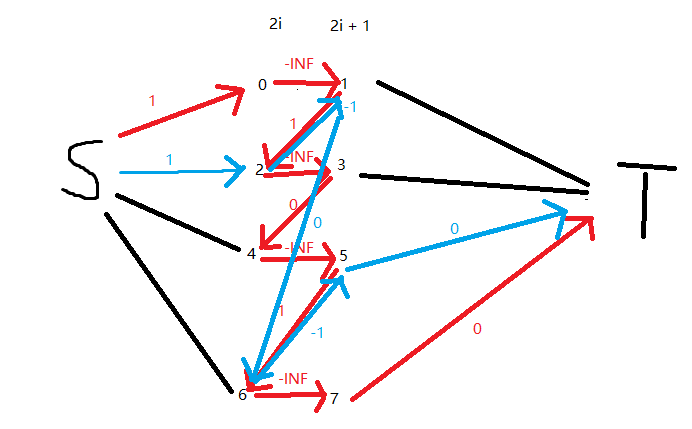
当 k = 2 时，引入新边 （S -> 2），它会走边（2 -> 1），这个边其实就是网络流提供给算法一种 “反悔” 的策略，如蓝色轨迹所示，其中（1 -> 2，2 -> 1）（5 -> 6，6 -> 5）两对边，全部抵消掉了。

那么其实在 k = 2 时，真正的策略如上图轨迹所示，我们可以将 k 当作 k 个放书的位置，每个位置互不影响，其中第一个位置存放 1 这本书，在第 0 天和第 3 天分别被借阅，第二个位置存放 2 这本书，在第 1 天和第 2 天分别被借阅 。

首先用 -INF 保证所有点都被按顺序访问到（第一次搜索时），在根据 k 的值，不断的做出 “反悔” 策略，最终达到最小费用。

注意：当判断到 dis[T] >= 0 时就要退出了，这个时候多加的 k 也毫无意义了。最后答案加上 n * INF。

code

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int MAXN = 1e5 + 10; //
const int MAXM = 2e5 + 5; // 注意扩张的边的数量
const ll INF = 1e9;
struct Edge {
    int to, next, cap, flow, cost;
} edge[MAXM * 4];
int head[MAXN], tol;
int pre[MAXN];
ll dis[MAXN];
bool vis[MAXN];
int N;
void init(int n) {
    N = n;
    tol = 0;
    memset(head, -1, sizeof head);
    memset(pre, 0, sizeof pre);
    memset(dis, 0, sizeof dis);
    memset(vis, 0, sizeof vis);
    memset(edge, 0, sizeof edge);
}
void addedge (int u, int v, int cap, int cost) {
    edge[tol] = Edge{v, head[u], cap, 0, cost};
    head[u] = tol++;
    edge[tol] = Edge{u, head[v], 0, 0, -cost};
    head[v] = tol++;
}
bool spfa(int s, int t) {
    queue<int>q;
    for(int i = 0; i < N; i++) {
        dis[i] = INF * INF;
        vis[i] = false;
        pre[i] = -1;
    }
    dis[s] = 0;
    vis[s] = true;
    q.push(s);
    while(!q.empty()) {
        int u = q.front();
        q.pop();
        vis[u] = false;
        for(int i = head[u]; i != -1; i = edge[i].next) {
            int v = edge[i]. to;
            if(edge[i].cap > edge[i].flow &&
                    dis[v] > dis[u] + edge[i].cost) {
                dis[v] = dis[u] + edge[i].cost;
                pre[v] = i;
                if(!vis[v]) {
                    vis[v] = true;
                    q.push(v);
                }
            }
        }
    }
    return dis[t] < 0;
}
int a[MAXN], b[MAXN];
int main() {
    int n, k;
    cin >> n >> k;
    for(int i = 0; i < n; i++) {
        cin >> a[i];
    }
    for(int i = 1; i <= n; i++) {
        cin >> b[i];
    }
    init(MAXN);
    int s = 2 * n, t = 2 * n + 1;
    for(int i = 0; i < n; i++) {
        addedge(s, 2 * i, 1, b[a[i]]);
        addedge(2 * i + 1, t, 1, 0);
        addedge(2 * i, 2 * i + 1, 1, -INF);
    }
    for(int i = 0; i < n; i++) {
        for(int j = i + 1; j < n; j++) {
            addedge(2 * i + 1, 2 * j, 1, a[i] == a[j] ? 0 : b[a[j]]);
        }
    }
    ll cost = 0;
    for(int i = 0; i < k; i++) {
        if(!spfa(s, t)) break;
        for(int j = pre[t]; j != -1; j = pre[edge[j^1].to]) {
            edge[j].flow++;
            edge[j^1].flow--;
        }
        cost += dis[t];
    }
    cout << cost + 1LL * n * INF<< endl;
    return 0;
}