poj1830--高斯消元
http://poj.org/problem?id=1830
某些开关的动作可能影响另一些开关的状态,因此以开关为节点,如果存在这种关系就加入一条有向边(开始我想成对称的了,浪费了很多时间- -),这样就构成了一个图,可以用邻接矩阵表示(但是要转置一下,后面细说)。当某个开关按下时,其自身状态改变,受其影响的开关的状态也改变。
用两个N维向量表示初始状态和结束状态,两者逐个元素异或,就得到了开关状态的变化。
以第一个样例输入为例分析,3个开关,两两相连,初始状态000,最终状态111,开关对应的邻接矩阵为
将对角线的0全部换成1,得矩阵A=
将矩阵每一列想象为一个开关按下后产生的效果(1表示状态翻转,0表示不变),比如,第二列就表示按下第二个开关,则第二个开关的本身状态要改变(这就是把对角线0换成1的原因),受第二个开关影响的开关j状态也要改变,恰好对应邻接矩阵中A[j, 2]=1
把A写成分块矩阵的形式,每一列作为一个子矩阵,则有A=[a1, a2, a3],此处ai均为列
向量,设第i个开关按下次数为xi,xi=0或1(开关按两下和没按是等效的,0/1就够了)
记初始状态b0=[0,0,0],最终状态b1=[1,1,1],则状态变化b=b0^b1=[1,1,1],这里b也是列
向量。目标就是求x1a1 + x2a2 +x3a3 = b的解的个数(此处的加是模2加,也就是异或,下同)
这个方程可以写成
下面就是解这个线性方程组
对增广矩阵[A b]做初等行变换,化成阶梯形(高斯消元法),如果存在[0,0,…,0,1]的行,就是无解;如果存在r行[0,0,…,0,0],就意味着有r个自由变量,因为这里的变量只取0/1,所以有2r个解;如果不存在[0,0,…,0,*],即把最后一行去掉后不存在全0行,则A为
满秩矩阵,则方程组有唯一解。
如果不理解这个地方,建议找本线性代数书,看一下线性方程组的解法,解的结构,通解
下面是我写的代码,能用,但很丑陋,自己都不忍心看,但懒得改了,至少暂时是不想改了
//poj1830--线性方程组高斯消元 //开关问题--xor #include <stdio.h> #include <string.h> #include <algorithm> #include <cmath> using namespace std; int b[35]; int A[35][35]; void elem_trans(int N){//对N*(N+1)的增广矩阵做行初等变换 for (int r = 0, col = 0; r < N - 1 && col <= N;) {//对前n-1行 if (A[r][col] == 0) {//可能需要做行交换 int i; for (i = r + 1; i < N; i++) {//从下一行开始找 if (A[i][col] == 1) { for (int j = col; j <= N; j++) {//行交换 swap(A[i][j], A[r][j]); } break; } } if (i == N) {//如果这一列下面所有的都为0 col++;//指针移到下一列 continue; }//else i != N,表示是break出来的,已经做完行交换 } //assert A[r][col] == 1 for (int r2 = r + 1; r2 < N; r2++) {//用第r行对下面的行消元 if (A[r2][col] == 1) { for (int j = col; j <= N; j++) { A[r2][j] ^= A[r][j]; } } } r++, col++; } } bool is_equal(int *x, int begin, int end, int val){ for (int i = begin; i < end; i++) { if (x[i] != val) { return false; } } return true; } int calc(int N){ for (int i = 0; i < N; i++) { if (is_equal(A[i], 0, N, 0)) { for (int j = i; j < N; j++) { if (A[j][N] == 1) { return -1;//impossible } } return 1 << (N - i);//pow(2, N - i);//有解,且有N-i个自由变量 } } return 1; } int main(int argc, const char *argv[]) { int K, N; scanf("%d", &K);//K组测试数据 for (int i = 0; i < K; i++) { scanf("%d", &N);//N个开关 memset(b, 0, sizeof(b)); memset(A, 0, sizeof(A)); for (int j = 0; j < N; j++) { scanf("%d", &b[j]); } for (int j = 0, tmp; j < N; j++) { scanf("%d", &tmp); b[j] ^= tmp;//b是初始状态和最终状态的异或,即状态的变化 } int s, t; while (scanf("%d%d", &s, &t) != EOF && s != 0) { A[t - 1][s - 1] = 1; } for (int j = 0; j < N; j++) { A[j][j] = 1; A[j][N] = b[j];//将b放到最后一列构成增广矩阵 } elem_trans(N); int res = calc(N); if (res < 0) { printf("Oh,it's impossible~!!\n"); }else{ printf("%d\n", res); } } return 0; }




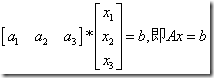

 浙公网安备 33010602011771号
浙公网安备 33010602011771号