字符串切分成回文子串所需的最少切分次数。

题目描述：给定一个字符串，计算出将该字符串切分成若干个回文子串所需的最少切分次数

思路：使用动态规划，每一次DP，从i向右扫描，每找到一个回文串就算一次DP的话，就可以转换为f[i]在区间[i,n-1]之间最小的切分数量。

状态转移方程：f(i) = min{f(j+1)+1,f(j)};

判断是否是回文串：也是使用DP，前面博客介绍过关于相关回文串的解法，这里不再详解

图示分析：

 

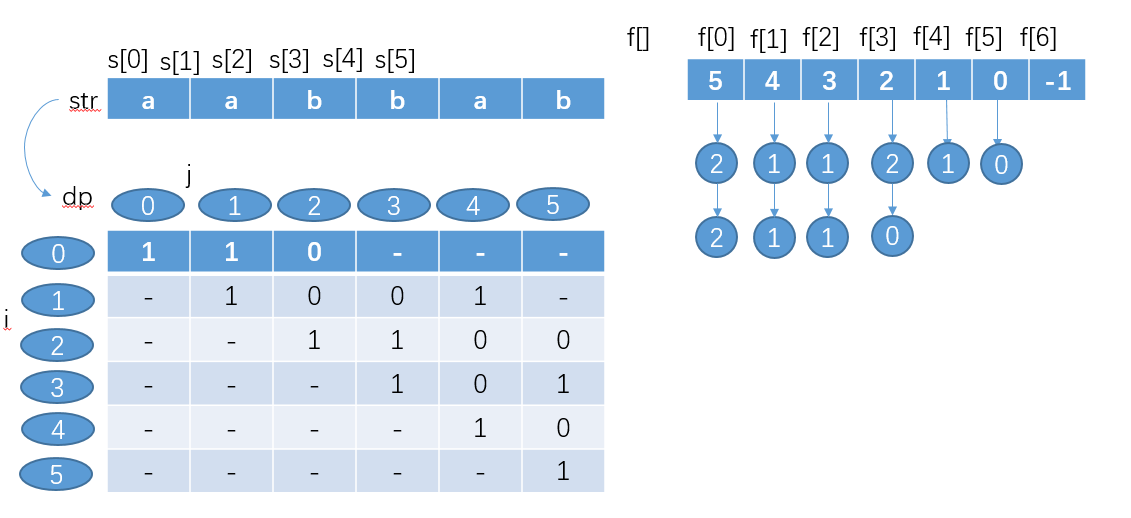
代码：

/**
 * 动态规划实现：切割字符串使得每一个子串为回文字符串，所需要的最少切割次数
 *
 */
public class Test7 {

    static String str = "aabbab";
    public static void main(String[] args) {
        System.out.println(minCut(str));
    }
    
    static int minCut(String str) {
        int len = str.length();
        int[] f = new int[len+1]; //最小分割的数组
        int[][] dp = new int[len][len]; //动态规划实现回文字符串判断
        /*
         * 初始化最坏情况  每一个字符串都作为单独的一个字符串作为回文字符串  这个时候f[0] = n-1-0
         * 需要n-1次切割  后续相同
         */
        for (int i = 0; i <= len; i++) {
            f[i] = len - 1 -i;
        }
        for (int i = len - 1; i >= 0; i--) {
            dp[i][i] = 1;
            for (int j = i; j < len; j++) {
                if(str.charAt(i) == str.charAt(j) && ((j - i < 2) || dp[i+1][j-1] == 1)) {
                    dp[i][j] = 1;
                    f[i] = Math.min(f[i], f[j+1]+1);
                }                
            }
        }
        return f[0];
    }
}