动态规划实现最大子序列连续和、积问题

最大连续子数组问题

参见https://www.kancloud.cn/wizardforcel/the-art-of-programming-by-july/97234描述的最大子序列之积问题

题目描述：给定一个数组，比如int[] arr = {-2, -1, -3, 4, -1, 2, 1, -5, 4} 求一个连续的子数组使得该连续的子数组和最大

时间复杂度：我们介绍一种时间复杂度为O(n)的算法

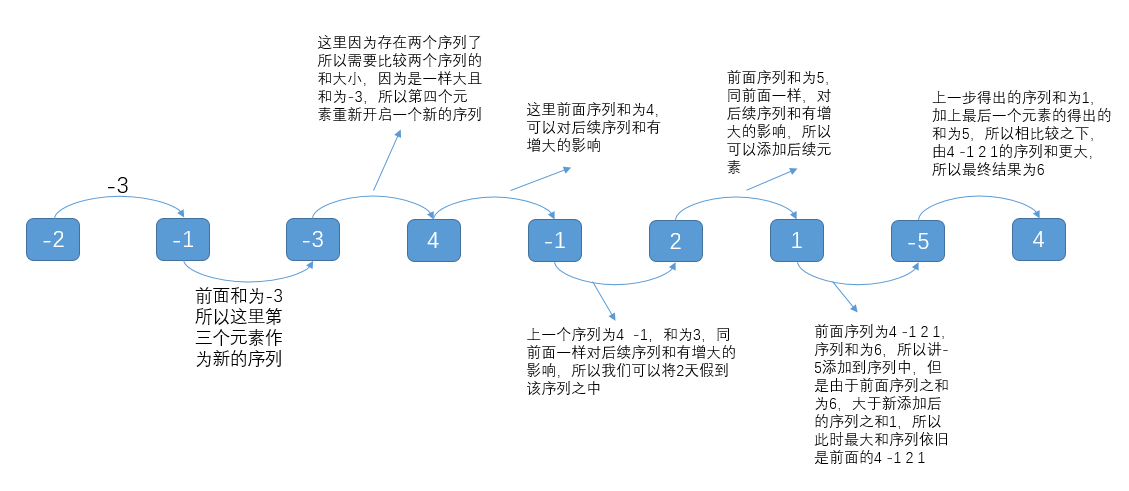
思路分析：首先，在我们从前往后遍历该数组的时候，对于数组里面的每一个元素，有两种选择：一种是作为在其之前的子序列之中，一种是自己作为一个新开的序列；如果原来的序列之和大于0，可以认为原来的序列之和对后续序列有增加作用的话，我们就可以将它添加到原来的序列当中，但是如果原来的序列之和已经等于0或者小于0的话，可以看书对后续序列之和只会起到削减的作用，这时候我们可以将新的元素作为其实序列的首元素，重新再增加一个序列。

状态方程：f[i] = max{f[i-1]+s[i],s[i]},result = max{f[i]};

给出图例分析：

　代码：

package cn.dp;

/**
 * 动态规划 实现最大子序列之和
 * @author 曹洋
 *
 */
public class Test6 {

    static int[] arr = {-2, -1, 3, 4, -1, 2, 1, -5, 4};
    static double[] arr1 = {-2.5,4,0,3,0.5,5,-1};
    
    public static void main(String[] args) {
        System.out.println("最大子序列之和：");
        System.out.println(maxAddSubArray(arr));
        System.out.println("最大子序列之积：");
        System.out.println(maxMutSubArray(arr1));
    }
    /**
     * 递推公式
     * f[i] = max{f[i-1]+s[i],s[i]}
     * @param arr
     * @return
     */
    static int maxAddSubArray(int[] arr) {
        int result = 0, f = 0;
        for (int i = 0; i < arr.length; i++) {
            f = Math.max(arr[i] + f, arr[i]);
            result = Math.max(result, f);
        }
        return result;
    }
    
    static double maxMutSubArray(double[] arr) {
        double result = 0, f = 0;
        for (int i = 0; i < arr.length; i++) {
            f = Math.max(arr[i]*f, arr[i]);
            result = Math.max(result, f);
        }
        return result;
    }
}