动态规划实现最优二分搜索树

最优二叉搜索树

　　(1）二叉搜索树 （二分检索树）二叉搜索树Ｔ是一棵二元树，它或者为空，或者其每个结点含有一个可以比较大小的数据元素，且有：

　　a·Ｔ的左子树的所有元素比根结点中的元素小；
　　b·Ｔ的右子树的所有元素比根结点中的元素大；
　　c·Ｔ的左子树和右子树也是二叉搜索树。

　　(2）最优二叉搜索树

　　给定一个n个关键字的已排序的序列K=<k 1 ,k 2 ,…,k n >（ 不失一般性，设k 1 <k 2 <…<k n ），对每个关键字k i ，都有一个概率p i 表示其搜索频率。根据k i和p i 构建一个二叉搜索树T，每个k i 对应树中的一个结点。若搜索对象x等于某个k i ，则一定可以在T中找到结点k i ；若x<k 1 或 x>k n 或 k i <x<k i+1 (1≤i<n), 则在T中将搜索失败。为此引入外部结点d 0 ,d 1 ,…,d n ，用来表示不在K中的值，称为伪结点。这里每个d d i i 代表一个区间， d 0 表示所有小于k 1 的值， d n 表示所有大于k n 的值，对于i=1,2,…,n-1，d i 表示所有在k i 和k i+1 之间的值。 同时每个d i 也有一个概率q q i i 表示搜索对象x恰好落入区间d i 的频率。

　　(3)例：设有n=5个关键字的集合，每个k i 的概率p i 和d i 的概率q i 如表所示：其中

 

　　

 　　基于该集合，两棵可能的二叉搜索树如下所示。

 　　

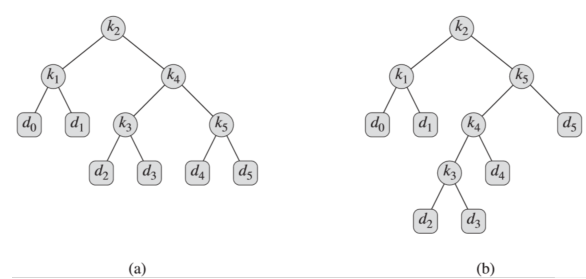
　　(4)二叉搜索树的期望搜索代价代价等于从根结点开始访问结点的数量。从根结点开始访问结点的数量等于结点在T中的深度+1； 二叉搜索树T的期望代价记depth T (i)为结点i在T中的深度，则T搜索代价的期望为：

 　　

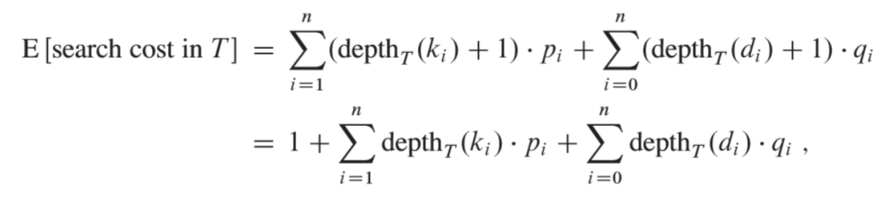
　　上面图中(a)的期望搜索代价为2.80。(b)的期望搜索代价为2.75。

最优二叉搜索树的定义对给定的概率集合，期望搜索代价最小的二叉搜索树称为最优二叉搜索树

　　(1)最优二叉搜索树的最优子结构：如果一棵 最优二叉搜索树T T有一棵包含关键字k i ,…,k j 的子树T’，则T’必然是包含关键字k i ,…,k j 和伪关键字d i-1 ,…,d j 的子问题的最优解。

　　(2)构造最优二叉搜索树利用最优二叉搜索树的最优子结构性来构造最优二叉搜索树。分析：

　　对给定的关键字k i ,…,k j ，若其最优二叉搜索树的根结点是k r（i≤r≤j），则k r 的左子树中包含关键字k i ,…,k r-1 及伪关键字d i-1,…,d r-1 ，右子树中将含关键字k i+1 ,…,k j 及伪关键字d r ,…,d j 。策略：检查所有可能的根结点k r （i≤r≤j），如果事先分别求出包含关键字k i ,…,k r-1 和关键字k r+1 ,…,k j 的最优二叉搜索子树，则可保证找到原问题的最优解。

　　(3)计算过程： 求解包含关键字k i ,…,k j 的最优二叉搜索树，其中，i≥1，j≤n 且 j≥i-1。

　　定义e[i,j]：为包含关键字k i ,…,k j 的最优二叉搜索树的期望搜索代价。e[1,n]为问题的最终解。

　　当j≥i时，我们需要从k i ,…,k j 中选择一个根结点k r ，其左子树包含关键字k i ,…,k r-1 且是最优二叉搜索子树，其右子树包含关键字k r+1 ,…,k j 且为最优二叉搜索子树。

 

　　(4)若k r 为包含关键字k i ,…,k j 的最优二叉搜索树(树根)，则其期望搜索代价与左、右子树的期望搜索代价e[i,r-1]和e[r+1,j]有如下递推关系：

 

　　其中，,所以得出

　　(5)有上面的分析，可以得到kr的递推公式

　　

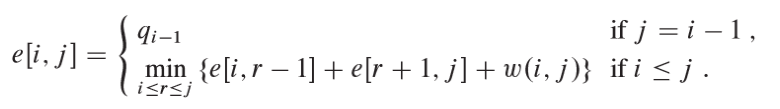
　　边界条件：j=i-1，存在e[i, i-1]和e[j+1, j]的边界情况。此时，子树不包含实际的关键字，而只包含伪关键字d i-1 ，其期望搜索代价为：

　　(6)构造最优二叉搜索树

　　定义root[i,j]，保存计算e[i, j]时使e[i, j]取得最小值的r。在求出e[1,n]后，利用root的记录构造出整棵最优二叉搜索树。

 　　(7)计算最优二叉搜索树的期望搜索代价

　　e[1..n+1,0..n]：

　　　　用于记录所有e[i,j]的值。注：e[n+1,n]对应伪关键字d n 的子树；e[1,0]对应伪关键字d 0 的子树。

　　root[1..n]：用于记录所有最优二叉搜索子树的根结点，包括整棵最优二叉搜索树的根。

　　w[1..n+1,0..n]：用于子树保存增加的期望搜索代价，且有

　　这样，对于Θ(n 2 )个w[i,j]，每个的计算时间仅为Θ(1)。

　　

　　上面算法是构造root表的算法

 举例说明

 　　(1)给出一组数据

　　

　　(2)根据求出w表的内容

　　

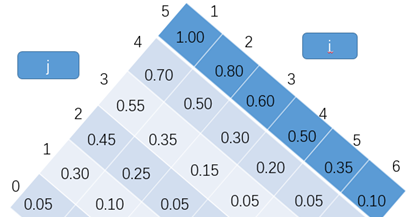
　　(3)根据求出e表的内容

　　 

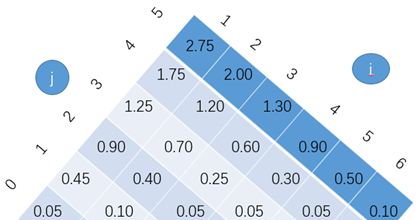
　　(4)最后根据上面的算法得出root表的内容

　　

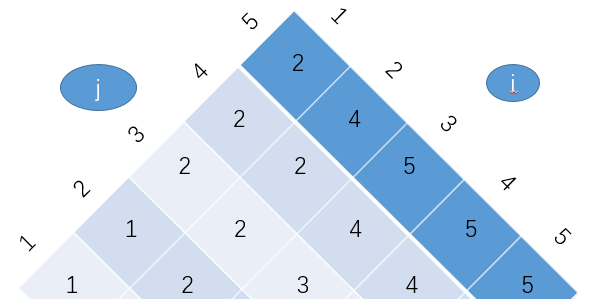
 　　(5)下面给出C++的最优二叉搜索树的代码实现

#include <iostream>
 
using namespace std;
 
const int MaxVal = 9999;
 
const int n = 5;
//搜索到根节点和虚拟键的概率
double p[n + 1] = {-1,0.15,0.1,0.05,0.1,0.2};
double q[n + 1] = {0.05,0.1,0.05,0.05,0.05,0.1};
 
int root[n + 1][n + 1];//记录根节点
double w[n + 2][n + 2];//子树概率总和
double e[n + 2][n + 2];//子树期望代价
 
void optimalBST(double *p,double *q,int n)
{
    //初始化只包括虚拟键的子树
    for (int i = 1;i <= n + 1;++i)
    {
        w[i][i - 1] = q[i - 1];
        e[i][i - 1] = q[i - 1];
    }
 
    //由下到上，由左到右逐步计算
    for (int len = 1;len <= n;++len)
    {
        for (int i = 1;i <= n - len + 1;++i)
        {
            int j = i + len - 1;
            e[i][j] = MaxVal;
            w[i][j] = w[i][j - 1] + p[j] + q[j];
            //求取最小代价的子树的根
            for (int k = i;k <= j;++k)
            {
                double temp = e[i][k - 1] + e[k + 1][j] + w[i][j];
                if (temp < e[i][j])
                {
                    e[i][j] = temp;
                    root[i][j] = k;
                }
            }
        }
    }
}
 
//输出最优二叉查找树所有子树的根
void printRoot()
{
    cout << "各子树的根：" << endl;
    for (int i = 1;i <= n;++i)
    {
        for (int j = 1;j <= n;++j)
        {
            cout << root[i][j] << " ";
        }
        cout << endl;
    }
    cout << endl;
}
 
//打印最优二叉查找树的结构
//打印出[i,j]子树，它是根r的左子树和右子树
void printOptimalBST(int i,int j,int r)
{
    int rootChild = root[i][j];//子树根节点
    if (rootChild == root[1][n])
    {
        //输出整棵树的根
        cout << "k" << rootChild << "是根" << endl;
        printOptimalBST(i,rootChild - 1,rootChild);
        printOptimalBST(rootChild + 1,j,rootChild);
        return;
    }
 
    if (j < i - 1)
    {
        return;
    }
    else if (j == i - 1)//遇到虚拟键
    {
        if (j < r)
        {
            cout << "d" << j << "是" << "k" << r << "的左孩子" << endl;
        }
        else
            cout << "d" << j << "是" << "k" << r << "的右孩子" << endl;
        return;
    }
    else//遇到内部结点
    {
        if (rootChild < r)
        {
            cout << "k" << rootChild << "是" << "k" << r << "的左孩子" << endl;
        }
        else
            cout << "k" << rootChild << "是" << "k" << r << "的右孩子" << endl;
    }
 
    printOptimalBST(i,rootChild - 1,rootChild);
    printOptimalBST(rootChild + 1,j,rootChild);
}
 
int main()
{
    optimalBST(p,q,n);
    printRoot();
    cout << "最优二叉树结构：" << endl;
    printOptimalBST(1,n,-1);
}

　　 输出结果