实现一个自动生成小学四则运算题目的命令行程序
1.github地址:https://github.com/foolishkylin/practice/tree/master/SimpleCompute
2.PSP表格
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
| Planning | 计划 | 10 | 10 |
| ·Estimate | ·估计这个任务需要多少时间 | 10 | 10 |
| Development | 开发 | 500 | 450 |
| ·Analysis | ·需求分析(包括学习新技术) | 60 | 70 |
| ·Design Spec | ·生成设计文档 | 10 | 10 |
| ·Design Review | ·设计复审(和同事审核设计文档) | 10 | 10 |
| ·Coding Standard | ·代码规范(为目前的开发设计合适的代码规范) | 10 | 10 |
| ·Design | ·具体设计 | 50 | 30 |
| ·Coding | ·具体编码 | 310 | 260 |
| ·Code Review | ·代码复审 | 20 | 20 |
| ·Tset | ·测试(自我测试,修改代码,提交修改) | 30 | 40 |
| Reporting | 报告 | 90 | 80 |
| ·Test Report | ·测试报告 | 30 | 30 |
| ·Size Measurement | ·计算工作量 | 30 | 30 |
| · Postmortem & Process Improvement Plan | ·事后总结,并提出过程修改计划 | 30 | 20 |
| 合计 | 600 | 540 |
3.需求分析
对题目分析可知,这次的作业是一个拓展分数的计算器,并且附加一些限制条件。
作业的核心部分是计数器,这部分可以经由数据结构-栈来实现,具体的思路和实现方法比较复杂,网上也有比较多的教程,此处不表。
而分数的部分,我们大致有三种思路,一种是把分数转化为小数进行计算,然后再输出结果为分数,这种思路要注意计算机本身的浮点数误差,要设法解决这个问题;二是在计算过程中,把运算数转化为同一分母下的分数进行运算,这种思路需要自己设计分数的结构,具体实现在网上已有许多参考资料;三是调用分数计算库,由于我们不重复造轮子,故采用了第三种思路。
对于附加条件部分:
- 计算过程中不能产生分数:在计算器运算过程中,遇到负数就退出;
- 结果为真分数:由于生成题目中的分数需处理为真分数,所以这里对结果进行相同的处理即可;
- 运算符不超过3个:我们通过限制运算数不超过4个来实现;
- 题目不能重复:这部分内容比较复杂,我们通过控制答案不重复来实现。
4.设计思路
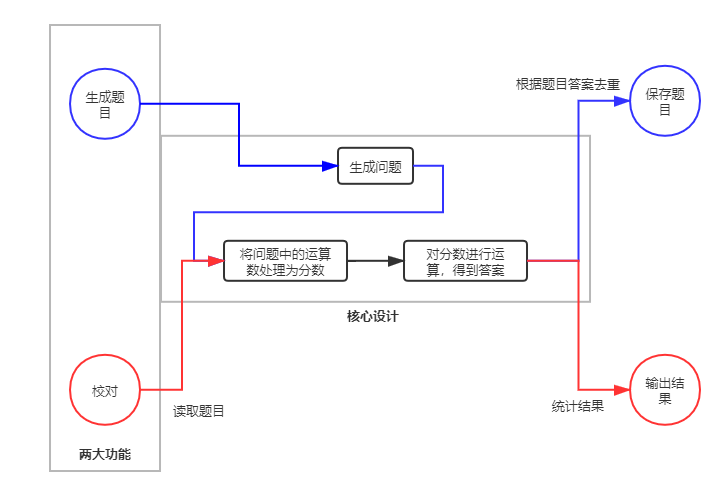
拿到问题后,将问题切割成一个个微小的单元(运算数、运算符),再对单元进行处理(分数化),最后把单元再组合成格式化的表达式,交给表达式计算函数进行运算。
5.项目设计图
def compute_equation(equation): """ :param equation: the str of equation such as '1 + 2 =' :return: the answer of equation in str fomat """ lequation = equation.split(' ') for it in range(len(lequation)): # fomat the equation to eval() etype = elem_type_judge(lequation[it]) if etype is 'f': if '`' in lequation[it]: tnum, frac = lequation[it].split('`') lequation[it]= '({} + fractions.Fraction(\'{}\'))'.format(tnum, frac) # 将假分数转化为真分数 else: lequation[it] = 'fractions.Fraction(\'{}\')'.format(lequation[it]) if etype is 'n': # 把自然数转化为分数 lequation[it] = 'fractions.Fraction(\'{}\')'.format(lequation[it]) elif etype is 'o': if lequation[it] is '÷': lequation[it] = '/' if lequation[it] is '×': lequation[it] = '*' elif etype is 'e': lequation[it] = '' fequation = ''.join(lequation) try: result = eval(fequation) # 调用计算函数 if result < 0: return '-1' else: return FfractoTfrac(result) # 将结果转化为真分数 except ValueError: print('the equation is wrong') return -1
7.回归测试
(1)测试思路是随机生成问题,我们随机取样进行人工校对。
1`3/10 × 5 + 1 + 3`1/5 = 10`7/10
2`4/5 × 5 - 3`2/5 - 6 = 4`3/5
2`3/5 ÷ 2`1/10 × 5 + 7 = 13`4/21
1 + 2`2/5 = 3`2/5
1`1/2 × 8 - 3`1/2 - 4 = 4`1/2
1 + 7/10 = 1`7/10
2 + 6 + 3`2/5 + 1`1/5 = 12`3/5
1 + 3`3/10 = 4`3/10
9 + 1`3/10 = 10`3/10
5 + 1`1/5 = 6`1/5
以上是随机抽取的10个问题,不难看出都是正确的。
(2)生成问题时的覆盖率:75%

(3)进行问题校对时的覆盖率:59%

8.性能测试
通过逐行分析可得如图所示:
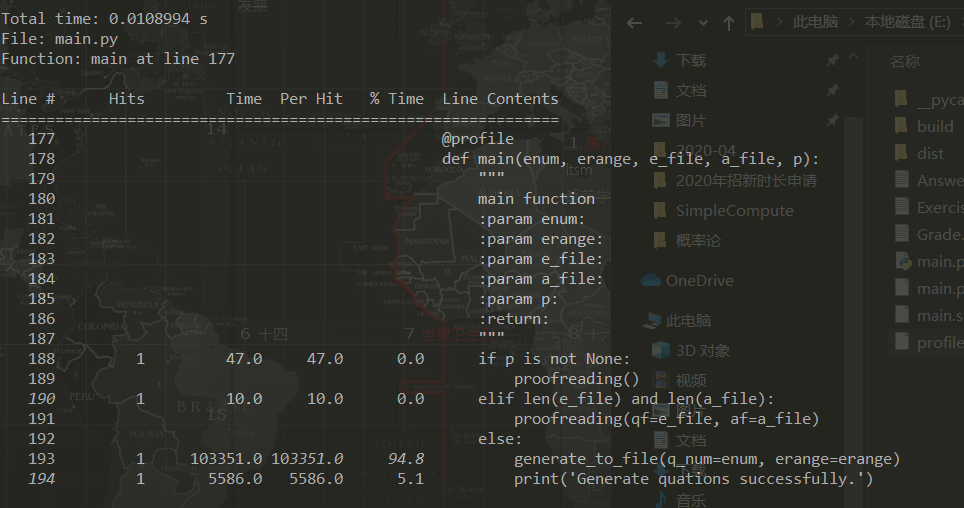
(生成题目时的性能分析)
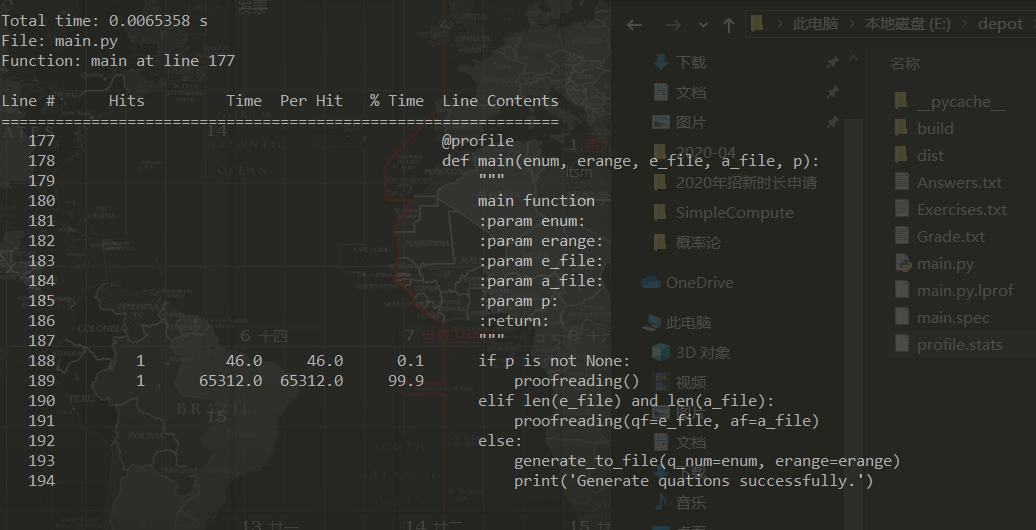
(进行校对时的性能分析)
可以看到最耗时的部分是生成题目的函数`generate_to_file`,其中涉及到较多的文件IO。
9.内存消耗分析
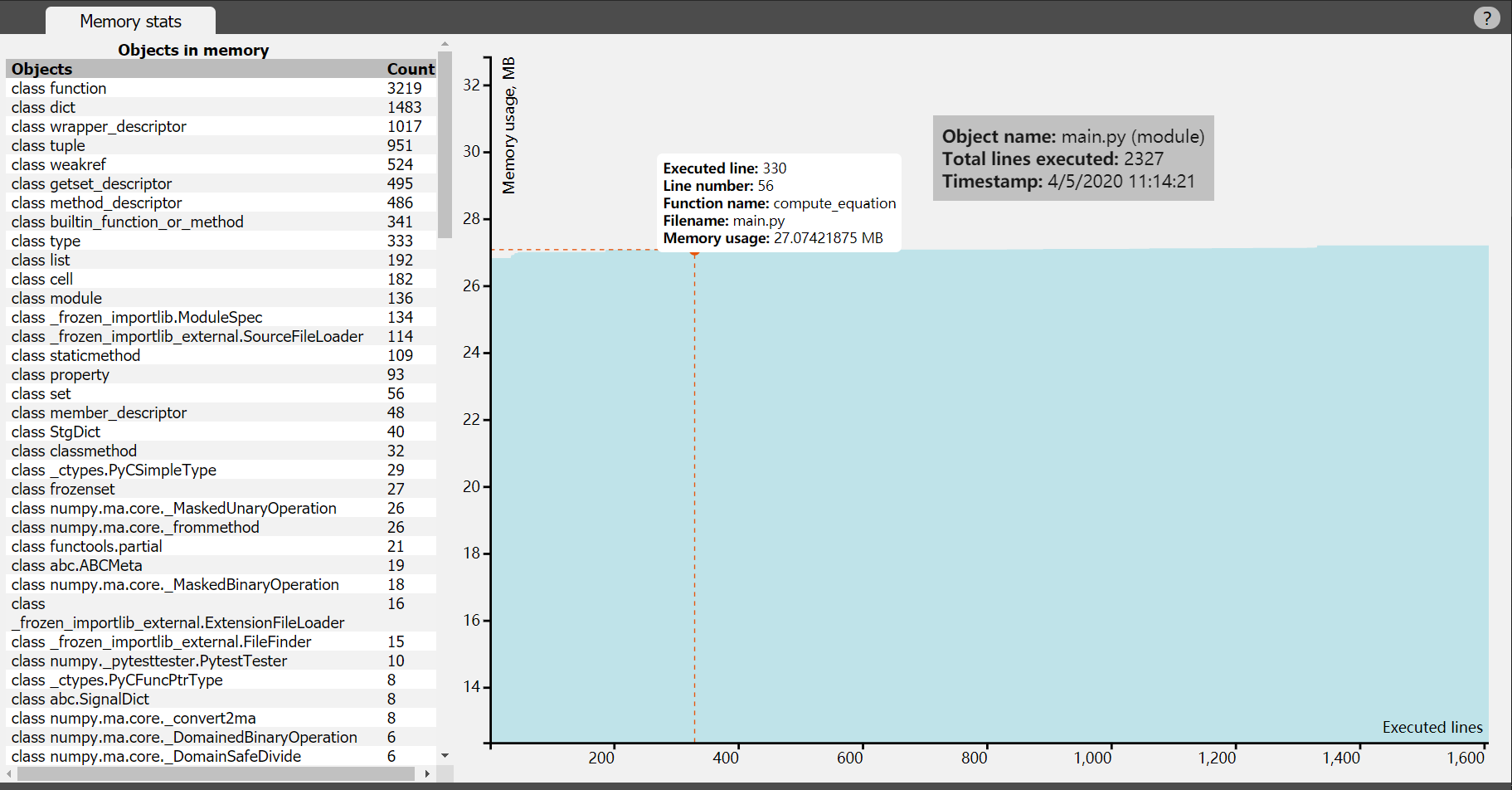
可以看出程序在执行过程中的内存消耗稳定,在27MB上下波动。
10.项目小结
辜仰淦:
第一次尝试结对合作,收获颇多,这次结对项目我们首先进行了开会讨论,研究项目的细节与大致的框架,确定方向,认真研究分析了需求,讨论了很多的方案。
在开发的过程中,我们积极交流,将遇到的问题与困难及时向对方反馈,认真聆听对方的意见,将我们各自的进度在做项目的时候总结汇报。以前在一个人开发时候总会遇到各种问题,而在结对项目中我们互相支持与鼓励,有问题一起分担,一起解决。如此种种让我体会到了队友的力量。
冯荣新:
我也是第一次和别人合作,通过这次合作,我对”众人拾柴火焰高“这句话有了更加深刻的理解,尤其是在讨论如何避免题目重复时,更是让我了解到软件工程这门课程的意义。在开发过程中,我们还要商讨函数里的参数问题,明白了统一的参数命名规则的意义,若没统一的命名规则,就有可能产生许多不必要的问题。
合作组合:辜仰淦 冯荣新

 浙公网安备 33010602011771号
浙公网安备 33010602011771号