圆方树初探
圆方树
圆方树是处理带环图的利器,它可以把原图转化成一个树的形态,所以很多树的性质都可以在其上加以利用。
圆方树实际上有两种。一种是仙人掌上圆方树,另一种是广义圆方树。
蒯图预警:接下来引用的图片全部来自网络,除了csacademy的图,没有一张不是蒯的(不蒯图会死.jpg)。感谢各位被动提供照片的神仙。
仙人掌上圆方树
首先定义仙人掌:任意一条边只会出现在一个环里面的无向连通图。Like this:
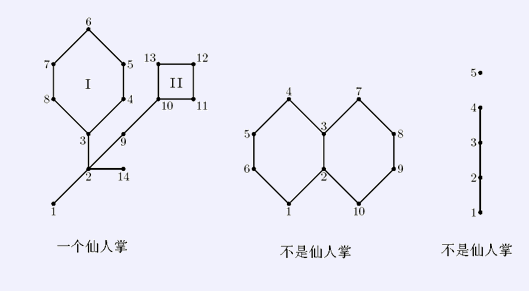
圆点就是原图上的点。
在一个仙人掌上,圆方树的构造方法是:
- 如果一条边在仙人掌中不属于任何一个环,那么就直接将圆方树上对应两圆点相连。
- 而对于每一个点双连通分量(也就是环),我们都构建出一个方点,将环上的点都向方点连一条边。这样每一个方点对应原图中的一个环。
Like this:
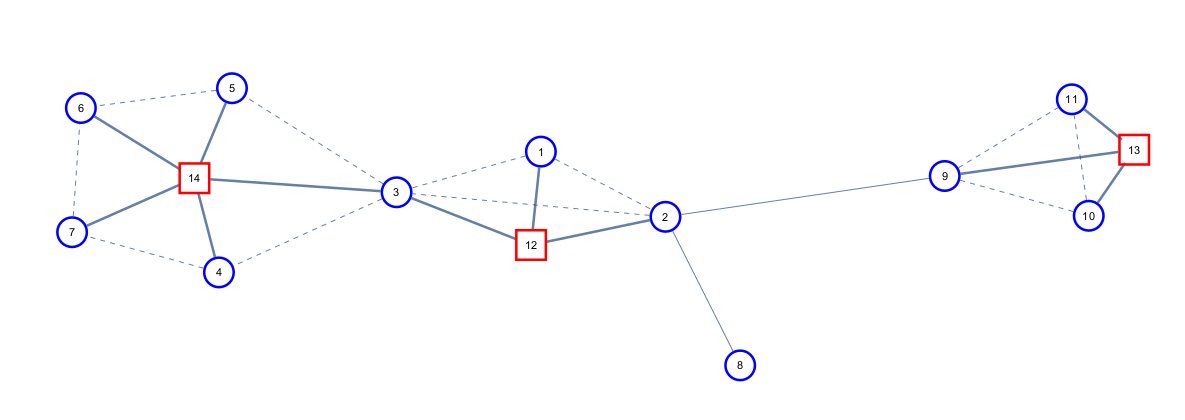
可以证明这样构造出来的新图一定是一棵树(引用自WC2017 immortalCO课件):

仙人掌上圆方树的构造
直接套用Tarjan找点双的方法实现。在这里,两个点一条边的情况并不看作点双,特殊考虑一下子。
inline void Tarjan(int nw,int pa=0){
dfn[nw]=low[nw]=++dfc;stk[++tp]=nw;
for(int to:r_E[nw])
if(to^pa){
if(!dfn[to]){
Tarjan(to,nw);
low[nw]=min(low[nw],low[to]);
if(dfn[nw]<=low[to]){
if(stk[tp]==to)E[nw].pb(to),E[to].pb(nw),--tp;//only two vertices
else{
++cnt;
for(int x=0;x^to;--tp){
x=stk[tp];
E[cnt].pb(x),E[x].pb(cnt);
}
E[cnt].pb(nw),E[nw].pb(cnt);
}
}
}
else low[nw]=min(low[nw],dfn[to]);
}
}
一些性质
-
方点不和方点直接连接。
-
圆方树是无根树,不管取哪个点为根,构造出来的圆方树形态一样。
-
首先定义:以 r 为根的仙人掌上的点 p 的子仙人掌是从仙人掌中去掉 p 到 r 的简单
路径上的所有边之后,p 所在的连通块。那么:以 r 为根的仙人掌中点 p 的子仙人掌就是圆方树以 r 为根时点 p 的
子树中的所有圆点。
广义圆方树
广义圆方树与仙人掌圆方树不同之处在于,认为两个点一条边的情况也是点双。
广义圆方树构造 Like this:
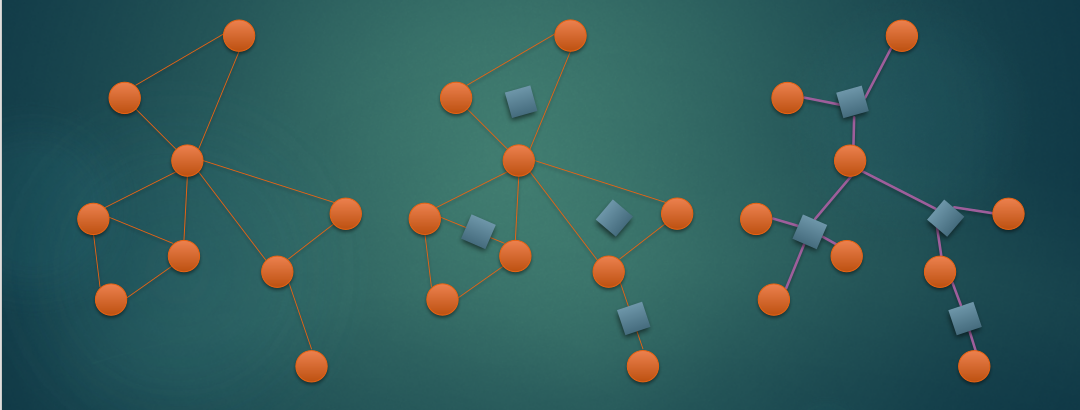
我们可以发现:现在圆方树上圆点只和方点相连,方点只和圆点相连。
值得注意的是:因为一般图不像仙人掌(一条边只在至多一个简单环中),所以它有可能是这样
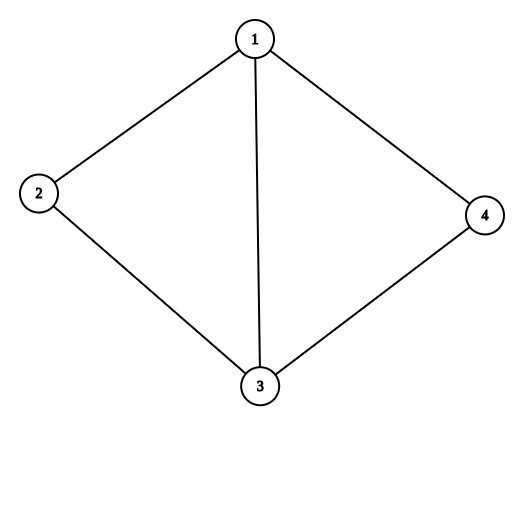
而他的点双只有这个(模拟一下Tarjan的过程就可以知道)
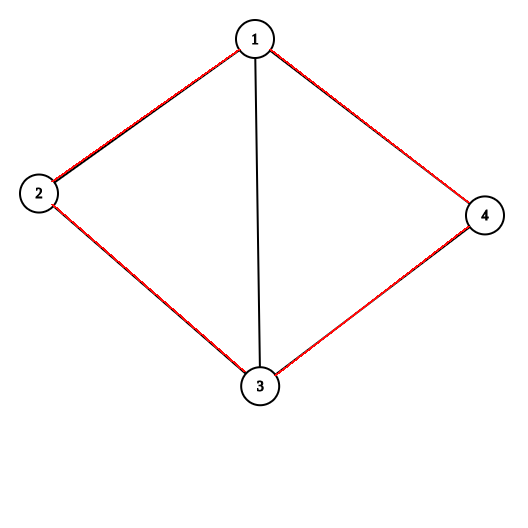
所以构造出的圆方树长这样:
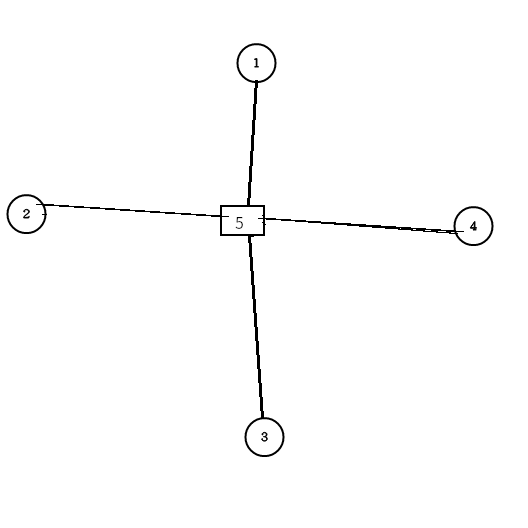
可以看到,原图中的(1,3)的边在圆方树中已经消失不见。所以除了像仙人掌那种一条边在至多一个环内的图外,一般图构造出的圆方树边的信息会有丢失。
广义圆方树的构造
一句话的区别。将两个点一条边的情况也看作点双。
inline void Tarjan(int nw,int pa=0){
dfn[nw]=low[nw]=++dfc;stk[++tp]=nw;
for(int to:r_E[nw])
if(to^pa){
if(!dfn[to]){
Tarjan(to,nw);
low[nw]=min(low[nw],low[to]);
if(dfn[nw]<=low[to]){
++cnt;
for(int x=0;x^to;--tp){
x=stk[tp];
E[cnt].pb(x),E[x].pb(cnt);
}
E[cnt].pb(nw),E[nw].pb(cnt);
}
}
else low[nw]=min(low[nw],dfn[to]);
}
}
例题
「APIO2018」铁人两项
Solution
固定\(s\)和\(f\),那么合法的\(c\)的数量就是\(s\),\(f\)之间简单路径的点集的并集减2(减掉\(s\),\(f\)本身)。
手玩一下可以发现一个结论:两圆点在圆方树上的路径的圆点点集,加上与路径上的方点相邻的圆点点集,就等于原图中两点所有简单路径的点集。
圆方树有一个技巧:路径统计时,给点附上恰当的权值。
例如这道题,给方点附上其对应点双大小,给圆点附上-1。
那么两圆点间路径的点权和就是圆点个数。因为方点贡献就是他的点双大小,而每个割点被重复统计多次,减去就好。
直接算还是不好算,可以考虑每个点对答案贡献:就是经过他的路径个数。树形dp即可。
Code
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
inline int read(){//be careful for long long!
register int x=0,f=1;register char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=0;ch=getchar();}
while(isdigit(ch)){x=x*10+(ch^'0');ch=getchar();}
return f?x:-x;
}
const int N=1e5+10;
int n,m,stk[N],tp,dfn[N],low[N],dfc,cnt,val[N<<1],siz[N<<1],num;
vector<int> G[N],E[N<<1];
ll ans;
inline void Tarjan(int nw){
dfn[nw]=low[nw]=++dfc;stk[++tp]=nw;++num;
for(int to:G[nw]){
if(!dfn[to]){
Tarjan(to);
low[nw]=min(low[nw],low[to]);
if(dfn[nw]==low[to]){
++cnt;
for(int x=0;x!=to;--tp){
x=stk[tp];++val[cnt];
E[cnt].push_back(x),E[x].push_back(cnt);
}
++val[cnt];
E[cnt].push_back(nw),E[nw].push_back(cnt);
}
}
else low[nw]=min(low[nw],dfn[to]);
}
}
inline void Dfs(int nw,int fa=0){
siz[nw]=(nw<=n);
for(int to:E[nw])
if(to^fa){
Dfs(to,nw);
ans+=2ll*val[nw]*siz[nw]*siz[to];
siz[nw]+=siz[to];
}
ans+=2ll*val[nw]*siz[nw]*(num-siz[nw]);
}
int main(){
n=read(),m=read();for(int i=1;i<=n;++i)val[i]=-1;
for(int i=1;i<=m;++i){
int u=read(),v=read();
G[u].push_back(v),G[v].push_back(u);
}
cnt=n;
for(int i=1;i<n;++i)
if(!dfn[i]){
tp=num=0,Tarjan(i);
Dfs(i);
}
printf("%lld\n",ans);
return 0;
}
CF1276B Two Fairs
Solution
把圆方树建出来,然后就显然了。直接将a,b两侧的子树内节点数相乘即可。
考虑两种情况:
- a,b没有祖孙关系。这一种ans就是\((siz[a]-1)\times (siz[b]-1)\)。
- a,b有祖孙关系。不失一般性地假设a是b的祖先。这是a一侧的子树不再是\(siz[a]-1\),应该是a子树以外的部分。设b往上走一直走到a儿子处的方点为s,ans就是\((n-siz[s]-1)*(siz[b]-1)\)。注意是a往下的第一个方点而不是圆点,这是我一开始没考虑清楚的地方。方点代表的点双上,不是a的点,都可以不经过a就到达b侧子树内。他们是不应计算进答案的。
tips: \(siz[]\)指的是子树内圆点个数。
Code
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
inline int read(){//be careful for long long!
register int x=0,f=1;register char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=0;ch=getchar();}
while(isdigit(ch)){x=x*10+(ch^'0');ch=getchar();}
return f?x:-x;
}
const int N=2e5+10,M=5e5+10;
int n,m,a,b,stk[N],tp,cnt,dfn[N],low[N],dfc,siz[N<<1],vis[N<<1],fa[N<<1];
vector<int> r_E[N],E[N<<1];
#define pb(x) push_back(x)
inline void Tarjan(int nw,int pa=0){
dfn[nw]=low[nw]=++dfc;stk[++tp]=nw;
for(int to:r_E[nw])
if(to^pa){
if(!dfn[to]){
Tarjan(to);
low[nw]=min(low[nw],low[to]);
if(dfn[nw]<=low[to]){
++cnt;
for(int x=0;x^to;--tp){
x=stk[tp];
E[cnt].pb(x),E[x].pb(cnt);
}
E[cnt].pb(nw),E[nw].pb(cnt);
}
}
else low[nw]=min(low[nw],dfn[to]);
}
}
inline void Dfs(int nw,int pa,int type){
vis[nw]=type;siz[nw]=(nw<=n);fa[nw]=pa;
if(nw==a)type=1;else if(nw==b)type=2;
for(int to:E[nw])
if(to^pa){
Dfs(to,nw,type);
siz[nw]+=siz[to];
}
}
int main(){
int T=read();
for(int t=1;t<=T;++t){
cnt=n=read(),m=read();a=read(),b=read();
for(int i=1;i<=n;++i)r_E[i].clear();
for(int i=1,tim=(n<<1);i<=tim;++i)E[i].clear();
for(int i=1;i<=m;++i){
int u=read(),v=read();
r_E[u].pb(v),r_E[v].pb(u);
}
memset(dfn,0,sizeof(int)*(n+1));
dfc=tp=0;Tarjan(1);
Dfs(1,0,0);
if(vis[a]==2){
int s=a;while(fa[s]!=b)s=fa[s];
printf("%lld\n",1ll*(siz[a]-1)*(n-siz[s]-1));
}
else if(vis[b]==1){
int s=b;while(fa[s]!=a)s=fa[s];
printf("%lld\n",1ll*(siz[b]-1)*(n-siz[s]-1));
}
else printf("%lld\n",1ll*(siz[a]-1)*(siz[b]-1));
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号