[JOISC 2016] 雇佣计划 题解
[JOISC 2016] 雇佣计划 题解
这里补充一篇自己的 \(n \log n\) 做法。
本蒟蒻打了两棵线段树，并且进行了繁琐的分类讨论，完全被标算的树状数组吊打 qwq
题意：
给定一个序列 \(a\)，有两种操作：
- 将 \(c\) 位置权值改为 \(d\)；
- 给定一个权值 \(b\)，定义集合 \(S = \{i | a_i \ge b\}\)，对于 \(\forall l, r \in S\)，如果 $ \forall j \in [l, r]$，有 \(j \in S\)，则 \(l,r\) 在一组内。求组数。
思路：
首先，我们并不关注每个 \(a\) 与 \(b\) 具体的值，只需要考虑他们之间的相对大小关系，所以我们可以把所有用到的权值全部离线。这样我们就可以把值域分为最多 \(4 \times 10^5\) 个档次。
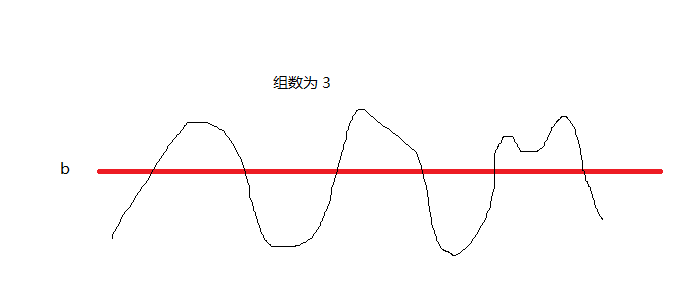
然后我们来考虑组数的转化。让我们把所有的 \(a_i\) 连起来，可以形成一个曲线。组数就是在曲线上面的连续段数。如图。
然后发现，这里的 \(b\) 可以看作一条扫描线，我们把 \(b\) 上面的部分赋值为 \(1\)，下面部分赋值为 \(0\)，则答案就是 \(1\) 连续段的个数。这个可以让 \(b\) 从上往下扫描，不断加入新的 \(1\)，然后用线段树维护。这样，我们可以求出一个 \(f\) 数组，表示如果没有修改，对于值域的每一档的答案。
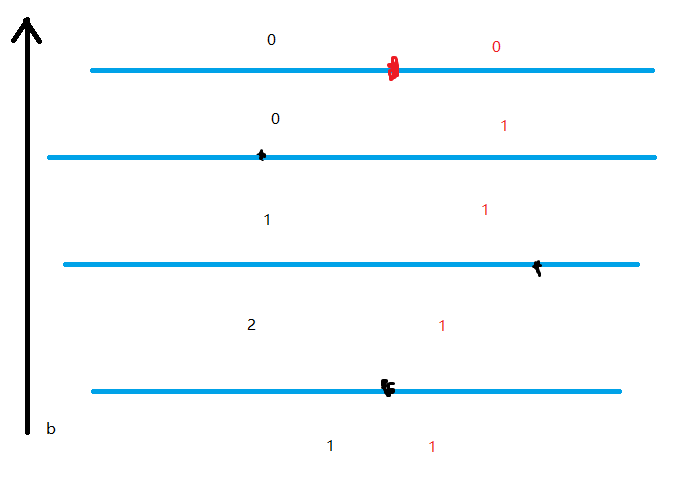
现在我们来考虑修改。我们发现，每一个修改的影响只与这个点和它两侧的点的权值相对大小有关，然后我就去分讨了，写了半天，比如下面这个例子，为了简化模型，我们现在只考虑这三个点的答案：
黑点代表修改前的点，红点代表修改后的点， 黑色的值为修改前的区间内的答案，红色的值为修改后区间内的答案。
对于每一个修改，影响到的区间内答案只有增加一或减小一，所以可以用线段树维护。
而实际上，左右两个点的大小关系是无所谓的，所以一共能分为两大类：权值增大与权值减小，每一类里还有三小类，即修改的点在两侧点下面，在两侧点之间，在两侧点上面。根据修改后的影响范围修改即可（其实这里还要稍微分下类，但是我懒了 xwx）。
具体的分类讨论还是看代码吧……反正很麻烦就对了，自己还是太菜了。
代码：
#include <bits/stdc++.h>
using namespace std;
const int N = 4e5 + 100;
inline int read() {
int x = 0;
char ch = getchar();
while (ch < '0' || ch > '9') ch = getchar();
while (ch >= '0' && ch <= '9') x = x * 10 + (ch - 48), ch = getchar();
return x;
}
int a[N], lsh[N];
int totl;
struct Questions {
int id, val;//id == 0: query.
} q[N];
int n, m;
struct xwx {
int val, id;
bool operator < (const xwx &b) const {
return val < b.val;
}
};
priority_queue<xwx> qu;
void prework() {//离散化所有出现的权值。
sort(lsh + 1, lsh + totl + 1);
totl = unique(lsh + 1, lsh + totl + 1) - lsh - 1;
for (int i = 1; i <= n; ++i) {
a[i] = lower_bound(lsh + 1, lsh + totl + 1, a[i]) - lsh;
qu.push((xwx) {
a[i], i
});
}
for (int i = 1; i <= m; ++i) {
q[i].val = lower_bound(lsh + 1, lsh + totl + 1, q[i].val) - lsh;
}
}
int f[N];
#define ls tr<<1
#define rs tr<<1 | 1
struct SegmentTree1 {//第一棵线段树，用来预处理 f
struct node {
int lc, rc;
int ans;
} tree[N << 2];
void push_up(int tr) {
tree[tr].ans = tree[ls].ans + tree[rs].ans - (tree[ls].rc & tree[rs].lc);
tree[tr].lc = tree[ls].lc;
tree[tr].rc = tree[rs].rc;
}
void modify(int tr, int L, int R, int pos) {
if (L == R) {
tree[tr] = (node) {
1, 1, 1
};
return;
}
int mid = (L + R) >> 1;
if (pos <= mid) {
modify(ls, L, mid, pos);
} else
modify(rs, mid + 1, R, pos);
push_up(tr);
}
int query() {
return tree[1].ans;
}
} s1;
struct SegmentTree2 {//第二棵线段树，用来处理修改。
struct node {
int val, tag;
} tree[N << 2];
//这里R就是值域totl 了
//标记永久化
void build(int tr, int L, int R) {
if (L == R) {
tree[tr].val = f[L];
return;
}
int mid = (L + R) >> 1;
build(ls, L, mid);
build(rs, mid + 1, R);
}
void modify(int tr, int L, int R, int lq, int rq, int val) {
if (lq <= L && R <= rq) {
tree[tr].tag += val;
return;
}
int mid = (L + R) >> 1;
if (lq <= mid)
modify(ls, L, mid, lq, rq, val);
if (mid < rq)
modify(rs, mid + 1, R, lq, rq, val);
}
int query(int tr, int L, int R, int pos) {
if (L == R) {
return tree[tr].tag + tree[tr].val;
}
int mid = (L + R) >> 1;
if (pos <= mid) {
return tree[tr].tag + query(ls, L, mid, pos);
} else {
return tree[tr].tag + query(rs, mid + 1, R, pos);
}
}
} s2;
int main() {
n = read(), m = read();
for (int i = 1; i <= n; ++i) {
a[i] = read();
lsh[++totl] = a[i];
}
for (int i = 1; i <= m; ++i) {
int op = read();
if (op == 1) {
q[i] = (Questions) {
0, read()
};
lsh[++totl] = q[i].val;
} else {
q[i].id = read(), q[i].val = read();
lsh[++totl] = q[i].val;
}
}
prework();
for (int i = totl; i >= 1; --i) {
while (qu.size() && qu.top().val >= i) {
s1.modify(1, 1, n, qu.top().id);//注意这里的R应该是n！不是值域！
qu.pop();
}
f[i] = s1.query();
}
s2.build(1, 1, totl);
for (int i = 1; i <= m; ++i) {
if (q[i].id) {
int id = q[i].id, del = q[i].val;
//这一部分建议结合曲线图来理解修改的区间（三个点的就够）
if (id == 1) {//首尾两个点特殊照顾一下。
if (a[id] < del) {//权值增加
if (del > a[id + 1]) {//如果增加的范围超过了右侧点
s2.modify(1, 1, totl, max(a[id + 1], a[id]) + 1, del, 1);
}
} else if (a[id] > del) {//权值减少
if (a[id] > a[id + 1]) {//如果减少前权值比右侧点大
s2.modify(1, 1, totl, max(a[id + 1], del) + 1, a[id], -1);
}
}
} else if (id == n) {//和 id == 1 类似
if (a[id] < del) {
if (del > a[id - 1]) {
s2.modify(1, 1, totl, max(a[id - 1], a[id]) + 1, del, 1);
}
} else if (a[id] > del) {
if (a[id] > a[id - 1]) {
s2.modify(1, 1, totl, max(a[id - 1], del) + 1, a[id], -1);
}
}
} else {
int mx = max(a[id - 1], a[id + 1]), mn = min(a[id - 1], a[id + 1]);
//我们只关心两侧点中较大的和较小的值为多少
if (a[id] < del) {//权值增加
if (a[id] < mn) {//修改前比较小值还要小
if (del <= mx) {//修改后没超过较大值
s2.modify(1, 1, totl, a[id] + 1, min(del, mn), -1);
} else {//超过了
s2.modify(1, 1, totl, a[id] + 1, mn, -1);
s2.modify(1, 1, totl, mx + 1, del, 1);
}
} else if (a[id] <= mx) {//修改前在两侧权值之间
if (del > mx) {//只有修改后超过较大值才会更新答案
s2.modify(1, 1, totl, mx + 1, del, 1);
}
} else {//修改前比较大值大
s2.modify(1, 1, totl, a[id] + 1, del, 1);
}
} else if (a[id] > del) {//权值减少
if (a[id] < mn) {//修改前低于较小值
s2.modify(1, 1, totl, del + 1, a[id], 1);
} else if (a[id] <= mx) {//修改前在两侧权值之间
if (del < mn) {
s2.modify(1, 1, totl, del + 1, mn, 1);
}
} else {//修改前在两侧权值上
if (del >= mn) {//如果修改后不低于较小值
s2.modify(1, 1, totl, max(mx, del) + 1, a[id], -1);
} else {
s2.modify(1, 1, totl, mx + 1, a[id], -1);
s2.modify(1, 1, totl, del + 1, mn, 1);
}
}
}
}
a[id] = del;
} else {
printf("%d\n", s2.query(1, 1, totl, q[i].val));//单点查询。
}
}
return 0;
}
